问题一，一个典型过桥问题：
小明一家5口人在夜晚过一座桥，小明过桥要1分钟，小明的弟弟过桥要3分钟，小明的爸爸过桥要6分钟，小明的妈妈过桥要8分钟，小明的爷爷过桥要12分钟；这座桥每次只能过2个人，因是夜晚，过桥时必须提着灯，小明有一只灯，点燃后30分钟会熄灭，问怎么样安排，才能保证小明一家在灯熄灭前过桥。
答案：
小明和弟弟过去，小明回来，4分钟
妈妈和爷爷过去，弟弟回来，15分钟
爸爸和小明过去，小明回来，7分钟
小明和弟弟过桥，3分钟
合计4+15+7+3=29分钟
问题二：如果有n个人过桥，一次只能过2个人，过桥必须提着灯，并且只有一只灯（这里不会熄灭）；求过桥所要的最少时间是？
现在我们把2（n>2）个人过桥的过程称为“过桥”，1个人提灯回来叫做“送灯”。
为了使整个过程耗时最少，那么就要尽量做到两点。一是送灯是1个人完成。那么这个人一定要最快。
二是过桥是2个人，因为是取两者耗时最多的，那么另一个人被吃掉的时间要尽量大。
如果两点能同时做到，那这样得到的耗时很有可能（未经证明不敢说一定）是最小的。
当n=1、2时，只有一次过桥，耗时为一固定值。
当n=3时，记3人分别为
,
,
。这里耗时<=<=,
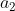
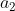
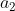
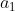
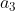
最佳方案为 操作 状态 耗时 过桥 ---- 送灯 ---- 过桥 ---- 总耗时 ++
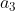
当n=4时，记4人耗时分别为,,,
。这里耗时<=<=<=,
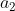
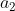
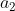
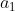
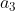
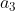
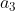
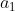
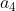
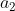
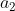
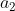
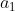
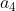
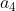
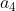
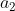
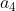
第一种方案，送灯要最快方案为 操作 状态 耗时 过桥 ---- 送灯 ---- 过桥 ---- 送灯 ---- 过桥 ---- 总耗时 2+++第二种，要吃掉时间最长方案为 操作 状态 耗时 过桥 ---- 送灯 ---- 过桥 ---- 送灯 ---- 过桥 ---- 总耗时 +3+
两种方案耗时差为（2+++)-(+3+)=+-2,所以当+>2时方案二更优，当+=2时方案一、二结果一样，当+<时方案一更优。可以列举其他方案，可以得出方案一二里必有一个为最优方案。当n>4时，记n个人耗时为,,.....,
，切依次不严格递增。很自然的可以想到最大耗时的几个人应该只进行一次过河。由n=4时可以知道送灯时间最短和被吃掉时间最长，并不能同时做到。但整个过程中，即使为了每次过桥尽可能吃掉一个最长的时间，也只需要2个不同的人送灯就可以做到，那么应该尽量选择和。这里假设过河方案为每次由、、
和将最大的
和送过河，直到n<=4。考虑到使被吃掉时间最长，应该和一起过河。那么和的过河方案为 操作 状态 耗时 ,过桥 （
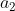
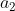
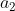
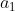
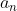
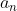
),， --- , 送灯 (),,, --- ,过桥 （), --- ,, 送灯 ,...,
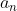
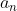
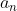
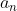
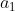
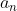
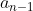
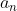
--- , 总耗时 +2+ 如果不和一起过河，那么这里只利用送灯，使和过河。 操作 状态 耗时 ,过桥 （),， --- , 送灯 (),,, --- ,过桥 （), --- ,, 送灯 ,..., --- , 总耗时 2++ 在这两种方案下，过河规模减少了2（少了，），同样当2<+时，和同时过河更优；当2=+时,两种方案耗时相同；当2>+时,和不一起过河更优。那么现在过桥方案为，当n>4时，每次最先将耗时最长的两个人送过河，如果2<=+，选择和同时过河，如果2>+，选择、分别和过河；直到n<=4为止，当n<=4时最优结果已经讨论得出。假设 "g(a_{1},a_{2},\cdots ,a_{n})")
为上述方案的耗时函数，这里可以看出和过河代价为 "g(a_{1},a_{2},a_{n-1},a_{n})")
-。也即= "g(a_{1},a_{2},\cdots ,a_{n-2})")
+-（n>4）;那么在这个方案下，过桥问题耗时的解记为：n=1时， "g(a_{1})")
=n=2时，=a_{2} "g(a_{1},a_{2})=a_{2}")
n=3时，=a_{1}+a_{2}+a_{3})
n=4时，=\begin{cases}&space;2a_{1}+a_{2}+a_{3}+a_{4}&space;&&space;\text{&space;if&space;}&space;a_{1}+a_{3}<2a_{2}&space;\\&space;a_{1}+3a_{2}+a_{4}&space;&&space;\text{&space;if&space;}&space;a_{1}+a_{3}&space;\geqslant&space;2a_{2}&space;\end{cases} "g(a_{1},a_{2},a_{3},a_{4})=\begin{cases} 2a_{1}+a_{2}+a_{3}+a_{4} & \text{ if } a_{1}+a_{3}<2a_{2} \\ a_{1}+3a_{2}+a_{4} & \text{ if } a_{1}+a_{3} \geqslant 2a_{2} \end{cases}")
n>4且n为奇数时，=g\left&space;(&space;a_{1},a_{2},a_{n-1}&space;,a_{n}&space;\right&space;)+\cdots&space;+g\left&space;(&space;a_{1},a_{2},a_{4}&space;,a_{5}&space;\right&space;)+g\left&space;(&space;a_{1},a_{2},a_{3}&space;\right&space;)-\frac{n-3}{2}a_{2} "g\left ( a_{1},a_{2},\cdots ,a_{n} \right )=g\left ( a_{1},a_{2},a_{n-1} ,a_{n} \right )+\cdots +g\left ( a_{1},a_{2},a_{4} ,a_{5} \right )+g\left ( a_{1},a_{2},a_{3} \right )-\frac{n-3}{2}a_{2}")
n>4且n为偶数时，=g\left&space;(&space;a_{1},a_{2},a_{n-1}&space;,a_{n}&space;\right&space;)+\cdots&space;+g\left&space;(&space;a_{1},a_{2},a_{5}&space;,a_{6}&space;\right&space;)+g\left&space;(&space;a_{1},a_{2},a_{3},a_{4}&space;\right&space;)-\frac{n-4}{2}a_{2} "g\left ( a_{1},a_{2},\cdots ,a_{n} \right )=g\left ( a_{1},a_{2},a_{n-1} ,a_{n} \right )+\cdots +g\left ( a_{1},a_{2},a_{5} ,a_{6} \right )+g\left ( a_{1},a_{2},a_{3},a_{4} \right )-\frac{n-4}{2}a_{2}")
三、那么
是否为过桥问题的最优解呢？接下来就对其进行证明。首先当n>2时（n=1和2是可以单独讨论），每次过桥和送灯后，过桥人数减一，最后一次不需要人回来送灯，所以有过桥次数为n-1次，送灯次数为n-2次;设
和
，耗时为人的过桥和送灯次数，显然有
，且
，
。设函数=\sum_{i=1}^{n}a_{i}x_{i} "s(x_{1},x_{2},\cdots ,x_{n})=\sum_{i=1}^{n}a_{i}x_{i}")
对应送灯的总时间，设函数 "max\left ( a,b \right )")
表示取
,
最大值,设函数=\frac{1}{2}\underset{\sum_{i=1}^{n}x_{i}=n-2,x_{i}\in&space;N}{min}\left&space;(&space;\sum_{i=1}^{n}\sum_{k=1,i_{k}\neq&space;i}^{x_{i}+1}max\left&space;(&space;a_{i},a_{i_{k}}&space;\right&space;)&space;\right&space;) "h\left ( x_{1},x_{2},\cdots ,x_{n} \right )=\frac{1}{2}\underset{\sum_{i=1}^{n}x_{i}=n-2,x_{i}\in N}{min}\left ( \sum_{i=1}^{n}\sum_{k=1,i_{k}\neq i}^{x_{i}+1}max\left ( a_{i},a_{i_{k}} \right ) \right )")
（其实就是在
个（
），最优的选择 "\left ( a_{i},a_{j} \right )")
（
），使得对所有的对取最大值的和最小）对应过桥的总时间。记=s+h "f(x_{1},x_{2},\cdots ,x_{n})=s+h")
，现在求
最小值。这里先讨论
的关系，首先有约束条件为，
。对于函数
，由于
，)
，所以在序列中，为了取值尽量小，那么使越是前面的取值要尽可能大，当
时，有a_{1})
。对于函数
，
（i<j）,假设
>，此时记为
，则在中至少存在着-个&space;k\neq&space;i,k\neq&space;j "max\left ( a_{j},a_{k} \right ) k\neq i,k\neq j")
，显然有\leq&space;max\left&space;(&space;a_{j},a_{k}&space;\right&space;) "max\left ( a_{i},a_{k} \right )\leq max\left ( a_{j},a_{k} \right )")
，故有
将中-个)
换成-个)
使得
。所以
一个序列，满足对（i<j）有
，使得函数取得最小值。同时对
，&space;(k\neq&space;i) "max\left ( a_{i},a_{k} \right ) (k\neq i)")
，必有
或
，使得\leq&space;max\left&space;(&space;a_{i},a_{k}&space;\right&space;)&space;(j=1orj=2) "max\left ( a_{j},a_{k} \right )\leq max\left ( a_{i},a_{k} \right ) (j=1或j=2)")
，也即当
，取最小值时，即
，函数可以取得最小值。综上，对于满足约束条件，时。 "\exists X_{1}\geq X_{2},X_{i}=0 (i\geq 3)")
,当 "f\left ( X_{1},X_{2},0,\cdots ,0 \right )")
取得最小值时，也是 "f\left ( x_{1},x_{2},\cdots ,x_{n} \right )")
的最小值。在上述条件下，接下来讨论
,
怎么分配能取到最小值。对于函数 "s\left ( X_{1},X_{2},0,\cdots ,0 \right )")
同上。对于函数 "s\left ( X_{1},X_{2},0,\cdots ,0 \right )")
，设所有
个，
个和每1个)
相互匹配求最大值和的所有可能值的集合为
，这里有 "h=min\left ( A \right )")
，假设
不与匹配求最大值，而与 "a_{j} (j\neq 1,j\neq 2)")
匹配，那么至少有
个不与匹配求最大值，任取一个，显然有（
，
，
只出现一次）。那么有+max\left&space;(&space;a_{i},a_{j}&space;\right&space;)\leq&space;max\left&space;(&space;a_{1},a_{i}&space;\right&space;)+max\left&space;(&space;a_{2},a_{j}&space;\right&space;) "max\left ( a_{1},a_{2} \right )+max\left ( a_{i},a_{j} \right )\leq max\left ( a_{1},a_{i} \right )+max\left ( a_{2},a_{j} \right )")
，也就有当所有的与匹配求最大值时，可以在集合中取到更小的值。若与匹配后，还有多余的，则在剩下的
个和每1个 "a_{i} (i\geq 3)")
中，如果
，则
，由于要两两不同匹配，剩下的个和每1个 （正好
个）一一匹配。如果
，当所有的分别与
一一匹配求最大值时，能在集合中取到更小的值。否则必有 "a_{i}\left ( 3+X_{1}-X_{2}\leq i\leq n \right )")
与匹配求最大值，  "a_{j}\left ( 3\leq j\leq 2+X_{1}-X_{2} \right )")
与  "a_{k}\left ( 3+X_{1}-X_{2}\leq k\leq n ,k\neq i\right )")
匹配求最大值，而+max\left&space;(&space;a_{i},a_{k}&space;\right&space;)\leq&space;max\left&space;(&space;a_{1},a_{i}&space;\right&space;)+max\left&space;(&space;a_{j},a_{k}&space;\right&space;) "max\left ( a_{1},a_{j} \right )+max\left ( a_{i},a_{k} \right )\leq max\left ( a_{1},a_{i} \right )+max\left ( a_{j},a_{k} \right )")
。所以当所有与匹配后剩下的分别与匹配求最大值时，可以在集合
中取到更小的值。对于剩下的（
个）
(不严格递增)，显然是依次相连的两两匹配可以取得最小值。这里可以首先看和，由于对
，
且不等，有+max\left&space;(&space;a_{i},a_{j}&space;\right&space;)\leq&space;max\left&space;(&space;a_{n},a_{i}&space;\right&space;)+max\left&space;(&space;a_{n-1},a_{j}&space;\right&space;) "max\left ( a_{n},a_{n-1} \right )+max\left ( a_{i},a_{j} \right )\leq max\left ( a_{n},a_{i} \right )+max\left ( a_{n-1},a_{j} \right )")
，所以和匹配到一起可以取得最小值，依次下去就可知道依次相连的两两匹配可以取得最小值。由于函数为集合的最小值，通过对取集合的最小值时，匹配方式的讨论,在
且 "X_{i}=0,(i\geq 3)")
时，我们可以进一步得出函数的表达形式为:=\left&space;(&space;X_{2}+1&space;\right&space;)max\left&space;(&space;a_{1},a_{2}&space;\right&space;)+\sum_{k=1}^{X_{1}-X_{2}}max\left&space;(&space;a_{1},a_{2+k}&space;\right&space;)+max\left&space;(&space;a_{3+X_{1}-X_{2}},a_{4+X_{1}-X_{2}}&space;\right&space;)+\cdots&space;+max\left&space;(&space;a_{n-1},a_{n}&space;\right&space;) "h\left ( X_{1},X_{2},0,\cdots ,0 \right )=\left ( X_{2}+1 \right )max\left ( a_{1},a_{2} \right )+\sum_{k=1}^{X_{1}-X_{2}}max\left ( a_{1},a_{2+k} \right )+max\left ( a_{3+X_{1}-X_{2}},a_{4+X_{1}-X_{2}} \right )+\cdots +max\left ( a_{n-1},a_{n} \right )")
所以=X_{1}a_{1}+X_{2}a_{2}+\left&space;(&space;X_{2}+1&space;\right&space;)max\left&space;(&space;a_{1},a_{2}&space;\right&space;)+\sum_{k=1}^{X_{1}-X_{2}}max\left&space;(&space;a_{1},a_{2+k}&space;\right&space;)+max\left&space;(&space;a_{3+X_{1}-X_{2}},a_{4+X_{1}-X_{2}}&space;\right&space;)+\cdots&space;+max\left&space;(&space;a_{n-1},a_{n}&space;\right&space;) "f\left ( X_{1},X_{2},0,\cdots ,0 \right )=X_{1}a_{1}+X_{2}a_{2}+\left ( X_{2}+1 \right )max\left ( a_{1},a_{2} \right )+\sum_{k=1}^{X_{1}-X_{2}}max\left ( a_{1},a_{2+k} \right )+max\left ( a_{3+X_{1}-X_{2}},a_{4+X_{1}-X_{2}} \right )+\cdots +max\left ( a_{n-1},a_{n} \right )")
当n为奇数时，&space;&=&space;a_{1}+max\left&space;(&space;a_{1},a_{2}&space;\right&space;)+max\left&space;(&space;a_{2},a_{3}&space;\right&space;)\\&space;&+\left&space;(&space;2a_{1}+max\left&space;(&space;a_{1},a_{4}&space;\right&space;)+max\left&space;(&space;a_{1},a_{5}&space;\right&space;)&space;\right&space;)+\cdots&space;+\left&space;(&space;2a_{1}+max\left&space;(&space;a_{1},a_{1+X_{1}-X_{2}}&space;\right&space;)+max\left&space;(&space;a_{1},a_{2+X_{1}-X{2}}&space;\right&space;)&space;\right&space;)&space;\\&space;&+\left&space;(&space;a_{1}+a_{2}+max\left&space;(&space;a_{1},a_{2}&space;\right&space;)+max\left&space;(&space;a_{3+X_{1}-X_{2}},a_{4+X_{1}-X_{2}}&space;\right&space;)&space;\right&space;)+\cdots&space;+\left&space;(&space;a_{1}+a_{2}+max\left&space;(&space;a_{1},a_{2}&space;\right&space;)+max\left&space;(&space;a_{n-1},a_{n}&space;\right&space;)&space;\right&space;)&space;\end{align*} "\begin{align*} f\left ( X_{1},X_{2},0,\cdots ,0 \right ) &= a_{1}+max\left ( a_{1},a_{2} \right )+max\left ( a_{2},a_{3} \right )\\ &+\left ( 2a_{1}+max\left ( a_{1},a_{4} \right )+max\left ( a_{1},a_{5} \right ) \right )+\cdots +\left ( 2a_{1}+max\left ( a_{1},a_{1+X_{1}-X_{2}} \right )+max\left ( a_{1},a_{2+X_{1}-X{2}} \right ) \right ) \\ &+\left ( a_{1}+a_{2}+max\left ( a_{1},a_{2} \right )+max\left ( a_{3+X_{1}-X_{2}},a_{4+X_{1}-X_{2}} \right ) \right )+\cdots +\left ( a_{1}+a_{2}+max\left ( a_{1},a_{2} \right )+max\left ( a_{n-1},a_{n} \right ) \right ) \end{align*}")
这里函数
第二行项数为 "\frac{1}{2}\left ( X_{1}-X{2}-1 \right )")
，第三行项数为。且随着，值的改变项数相应增减（总项数不变）。令
，
，现在记 "f\left ( X \right )")
为的最小值。当时
，有-f\left&space;(&space;X&space;\right&space;)&=2a_{1}+max\left&space;(&space;a_{1},a_{3+X-Y}&space;\right&space;)+max\left&space;(&space;a_{1},a_{4+X-Y}&space;\right&space;)-\left&space;(&space;a_{1}+a_{2}+max\left&space;(&space;a_{1},a_{2}&space;\right&space;)+max\left&space;(&space;a_{3+X-Y},a_{4+X-Y}&space;\right&space;)&space;\right&space;)\\&space;&=&space;a_{1}+a_{3+X-Y}-2a_{2}\geq&space;0&space;\end{align*} "\begin{align*} f\left ( X+1 \right )-f\left ( X \right )&=2a_{1}+max\left ( a_{1},a_{3+X-Y} \right )+max\left ( a_{1},a_{4+X-Y} \right )-\left ( a_{1}+a_{2}+max\left ( a_{1},a_{2} \right )+max\left ( a_{3+X-Y},a_{4+X-Y} \right ) \right )\\ &= a_{1}+a_{3+X-Y}-2a_{2}\geq 0 \end{align*}")
此时有 "a_{1}+a_{i}-2a_{2}\geq 0\left ( 3+X-Y\leq i\leq n \right )")
当时
，有-f\left&space;(&space;X&space;\right&space;)&space;&=a_{1}+a_{2}+max\left&space;(&space;a_{1},a_{2}&space;\right&space;)+max\left&space;(&space;a_{1+X-Y},a_{2+X-Y}&space;\right&space;)-\left&space;(&space;2a_{1}+max\left&space;(&space;a_{1},a_{1+X-Y}&space;\right&space;)+max\left&space;(&space;a_{1},a_{2+X-Y}&space;\right&space;)&space;\right&space;)&space;\\&space;&=&space;2a_{2}-\left&space;(&space;a_{1}+a_{1+X-Y}&space;\right&space;)\geq&space;0&space;\end{align*} "\begin{align*} f\left ( X-1 \right )-f\left ( X \right ) &=a_{1}+a_{2}+max\left ( a_{1},a_{2} \right )+max\left ( a_{1+X-Y},a_{2+X-Y} \right )-\left ( 2a_{1}+max\left ( a_{1},a_{1+X-Y} \right )+max\left ( a_{1},a_{2+X-Y} \right ) \right ) \\ &= 2a_{2}-\left ( a_{1}+a_{1+X-Y} \right )\geq 0 \end{align*}")
此时有\geq&space;0\left&space;(&space;3\leq&space;i\leq&space;2+X-Y&space;\right&space;) "2a_{2}-\left ( a_{1}+a_{i} \right )\geq 0\left ( 3\leq i\leq 2+X-Y \right )")
所以有&space;&=g\left&space;(&space;a_{1},a_{2},a_{3}&space;\right&space;)+\left&space;(&space;g\left&space;(&space;a_{1}+a_{2}+a_{4}+a_{5}&space;\right&space;)-a_{2}&space;\right&space;)+\cdots&space;+\left&space;(&space;g\left&space;(&space;a_{1}+a_{2}+a_{n-1}+a_{n}&space;\right&space;)-a_{2}&space;\right&space;)&space;\\&space;&=g\left&space;(&space;a_{1},a_{2},a_{3}&space;\right&space;)+g\left&space;(&space;a_{1}+a_{2}+a_{4}+a_{5}&space;\right&space;)+\cdots&space;+g\left&space;(&space;a_{1}+a_{2}+a_{n-1}+a_{n}&space;\right&space;)-\frac{n-3}{2}a_{2}&space;\\&space;&=&space;g\left&space;(&space;a_{1},a_{2},\cdots&space;,a_{n}&space;\right&space;)&space;\end{align*} "\begin{align*} f\left ( X \right ) &=g\left ( a_{1},a_{2},a_{3} \right )+\left ( g\left ( a_{1}+a_{2}+a_{4}+a_{5} \right )-a_{2} \right )+\cdots +\left ( g\left ( a_{1}+a_{2}+a_{n-1}+a_{n} \right )-a_{2} \right ) \\ &=g\left ( a_{1},a_{2},a_{3} \right )+g\left ( a_{1}+a_{2}+a_{4}+a_{5} \right )+\cdots +g\left ( a_{1}+a_{2}+a_{n-1}+a_{n} \right )-\frac{n-3}{2}a_{2} \\ &= g\left ( a_{1},a_{2},\cdots ,a_{n} \right ) \end{align*}")
当n为偶数时，同理=g\left&space;(&space;a_{1},a_{2},\cdots&space;,a_{n}&space;\right&space;) "f\left ( X \right )=g\left ( a_{1},a_{2},\cdots ,a_{n} \right )")
。综上当n>2时有=f_{min}\left&space;(&space;X_{1},X_{2},0,\cdots&space;,0&space;\right&space;)=f\left&space;(&space;X&space;\right&space;)=g\left&space;(&space;a_{1},a_{2},\cdots&space;,a_{n}&space;\right&space;) "f_{min}\left ( x_{1},x_{2},\cdots ,x_{n} \right )=f_{min}\left ( X_{1},X_{2},0,\cdots ,0 \right )=f\left ( X \right )=g\left ( a_{1},a_{2},\cdots ,a_{n} \right )")
当n>2时，由定义可知=g\left&space;(&space;a_{1},a_{2},\cdots&space;,a_{n}&space;\right&space;) "f_{min}\left ( x_{1},x_{2},\cdots ,x_{n} \right )=g\left ( a_{1},a_{2},\cdots ,a_{n} \right )")
必为过桥问题耗时的下界，又是过桥问题一个方案的耗时解。所以函数为过桥问题的最小耗时。当n=1,2时，同样也是过桥问题的最小耗时。
