hiho1192 简单的树嵌入（构造题）

题目链接

#1192 : 简单的树嵌入

时间限制:10000ms

单点时限:1000ms

内存限制:256MB

描述

给定一棵n个点的无权树。定义两点i, j(0 ≤ i, j ≤ n - 1)间的距离d(i, j)为两点间树上最短路径的长度(边数)。

我们需要将这n个点映射到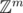中的向量v0 = (v0, 0, ..., v0, m - 1), ..., vn - 1 = (vn - 1, 0, ..., vn - 1, m - 1)。定义两向量vi, vj间的L1距离为

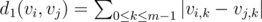
我们希望对于所有0 ≤ i, j ≤ n - 1有d(i, j) = d1(vi, vj)。

输入

第一行n。下面n - 1行，其中第i行为两个空格分开的整数xi, yi，表示点xi和yi间有一条边。

n ≤ 100. 0 ≤ xi, yi ≤ n - 1.

输出

第一行m。下面n行，其中第i行为m个空格分开的整数vi - 1, 0, ..., vi - 1, m - 1。

要求m ≤ 100且 - 100 ≤ vi, j ≤ 100。并且，对于所有0 ≤ i, j ≤ n - 1，d(i, j) = d1(vi, vj)。

如果有多解，输出任意一组满足要求的解即可。

样例输入

30 11 2

样例输出

20 01 01 1

题解：

假设只有一个点，那么构造这个点的向量为 {0} 即可。如果第二个点和这个点连了一条边，即可构造这个点的向量为{0,1}，第一个点的向量结尾增加一个0位 {0,0} 。以此类推。如果第i个点和第j个点（i>j）连了一条边，即先把第j个点的向量付给第i个点，第i个点的向量新增一维为1，其它点的向量也新增一维为0。由于新增了一维，这一维只有第i个点为1，所以增加这一维对其它点的影响是一样的，而其它点之间不会因为增加这一维而受到影响。每个点增加一维，那么向量最多n维。对图进行bfs，按照上面的方法构造即可。

代码如下：

#include<iostream>#include<stdio.h>#include<algorithm>#include<math.h>#include<queue>#include<string>#include<string.h>#include<stack>#include<vector>#include<set>#include<map>typedef long long LL;typedef unsigned long long LLU;double pi = acos(-1);const int nn = 110000;const int inf = 0x3fffffff;const int inff = 0x3fffffff;const LL mod = 1000000003;using namespace std;int n;struct node{    int en,next;}E[210];int p[110],num;int ans[110][110];int len[110];void init(){    memset(p,-1,sizeof(p));    num=0;}void add(int st,int en){    E[num].en=en;    E[num].next=p[st];    p[st]=num++;    E[num].en=st;    E[num].next=p[en];    p[en]=num++;}bool use[nn];queue<int>que;int main(){    int i,j;    while(scanf("%d",&n)!=EOF)    {        init();        int u,v;        for(i=1;i<n;i++)        {            scanf("%d%d",&u,&v);            add(u,v);        }        memset(ans,0,sizeof(ans));        memset(len,0,sizeof(len));        memset(use,false,sizeof(use));        use[0]=true;        len[0]=1;        que.push(0);        int cnt=1;        while(que.size())        {            int sta=que.front();            que.pop();            for(i=p[sta];i+1;i=E[i].next)            {                int w=E[i].en;                if(!use[w])                {                    use[w]=true;                    for(j=0;j<len[sta];j++)                    {                        ans[w][j]=ans[sta][j];                    }                    ans[w][cnt++]=1;                    len[w]=cnt;                    que.push(w);                }            }        }        printf("%d\n",cnt);        for(i=0;i<n;i++)        {            for(j=0;j<cnt;j++)            {                printf("%d%c",ans[i][j],j==cnt-1?'\n':' ');            }        }    }    return 0;}