矩阵乘法的Strassen算法
来源:互联网 发布:银行数据录入员好学吗 编辑:程序博客网 时间:2024/04/25 12:00
题目描述
请编程实现矩阵乘法,并考虑当矩阵规模较大时的优化方法。
思路分析
根据wikipedia上的介绍:两个矩阵的乘法仅当第一个矩阵B的列数和另一个矩阵A的行数相等时才能定义。如A是m×n矩阵和B是n×p矩阵,它们的乘积AB是一个m×p矩阵,它的一个元素其中 1 ≤ i ≤ m, 1 ≤ j ≤ p。
值得一提的是,矩阵乘法满足结合律和分配率,但并不满足交换律,如下图所示的这个例子,两个矩阵交换相乘后,结果变了:
下面咱们来具体解决这个矩阵相乘的问题。
解法一、暴力解法
其实,通过前面的分析,我们已经很明显的看出,两个具有相同维数的矩阵相乘,其复杂度为O(n^3),参考代码如下:
- //矩阵乘法,3个for循环搞定
- void Mul(int** matrixA, int** matrixB, int** matrixC)
- {
- for(int i = 0; i < 2; ++i)
- {
- for(int j = 0; j < 2; ++j)
- {
- matrixC[i][j] = 0;
- for(int k = 0; k < 2; ++k)
- {
- matrixC[i][j] += matrixA[i][k] * matrixB[k][j];
- }
- }
- }
- }
解法二、Strassen算法
在解法一中,我们用了3个for循环搞定矩阵乘法,但当两个矩阵的维度变得很大时,O(n^3)的时间复杂度将会变得很大,于是,我们需要找到一种更优的解法。
一般说来,当数据量一大时,我们往往会把大的数据分割成小的数据,各个分别处理。遵此思路,如果丢给我们一个很大的两个矩阵呢,是否可以考虑分治的方法循序渐进处理各个小矩阵的相乘,因为我们知道一个矩阵是可以分成更多小的矩阵的。
如下图,当给定一个两个二维矩阵A B时:
这两个矩阵A B相乘时,我们发现在相乘的过程中,有8次乘法运算,4次加法运算:
矩阵乘法的复杂度主要就是体现在相乘上,而多一两次的加法并不会让复杂度上升太多。故此,我们思考,是否可以让矩阵乘法的运算过程中乘法的运算次数减少,从而达到降低矩阵乘法的复杂度呢?答案是肯定的。
1969年,德国的一位数学家Strassen证明O(N^3)的解法并不是矩阵乘法的最优算法,他做了一系列工作使得最终的时间复杂度降低到了O(n^2.80)。
他是怎么做到的呢?还是用上文A B两个矩阵相乘的例子,他定义了7个变量:
如此,Strassen算法的流程如下:
- 两个矩阵A B相乘时,将A, B, C分成相等大小的方块矩阵:
;
- 可以看出C是这么得来的:
- 现在定义7个新矩阵(读者可以思考下,这7个新矩阵是如何想到的):
- 而最后的结果矩阵C 可以通过组合上述7个新矩阵得到:
表面上看,Strassen算法仅仅比通用矩阵相乘算法好一点,因为通用矩阵相乘算法时间复杂度是,而Strassen算法复杂度只是。但随着n的变大,比如当n >> 100时,Strassen算法是比通用矩阵相乘算法变得更有效率。
具体实现的伪代码如下:
Strassen (N,MatrixA,MatrixB,MatrixResult) //splitting input Matrixes, into 4 submatrices each. for i <- 0 to N/2 for j <- 0 to N/2 A11[i][j] <- MatrixA[i][j]; //a矩阵块 A12[i][j] <- MatrixA[i][j + N / 2]; //b矩阵块 A21[i][j] <- MatrixA[i + N / 2][j]; //c矩阵块 A22[i][j] <- MatrixA[i + N / 2][j + N / 2];//d矩阵块 B11[i][j] <- MatrixB[i][j]; //e 矩阵块 B12[i][j] <- MatrixB[i][j + N / 2]; //f 矩阵块 B21[i][j] <- MatrixB[i + N / 2][j]; //g 矩阵块 B22[i][j] <- MatrixB[i + N / 2][j + N / 2]; //h矩阵块 //here we calculate M1..M7 matrices . //递归求M1 HalfSize <- N/2 AResult <- A11+A22 BResult <- B11+B22 Strassen( HalfSize, AResult, BResult, M1 ); //M1=(A11+A22)*(B11+B22) p5=(a+d)*(e+h) //递归求M2 AResult <- A21+A22 Strassen(HalfSize, AResult, B11, M2); //M2=(A21+A22)B11 p3=(c+d)*e //递归求M3 BResult <- B12 - B22 Strassen(HalfSize, A11, BResult, M3); //M3=A11(B12-B22) p1=a*(f-h) //递归求M4 BResult <- B21 - B11 Strassen(HalfSize, A22, BResult, M4); //M4=A22(B21-B11) p4=d*(g-e) //递归求M5 AResult <- A11+A12 Strassen(HalfSize, AResult, B22, M5); //M5=(A11+A12)B22 p2=(a+b)*h //递归求M6 AResult <- A21-A11 BResult <- B11+B12 Strassen( HalfSize, AResult, BResult, M6); //M6=(A21-A11)(B11+B12) p7=(c-a)(e+f) //递归求M7 AResult <- A12-A22 BResult <- B21+B22 Strassen(HalfSize, AResult, BResult, M7); //M7=(A12-A22)(B21+B22) p6=(b-d)*(g+h) //计算结果子矩阵 C11 <- M1 + M4 - M5 + M7; C12 <- M3 + M5; C21 <- M2 + M4; C22 <- M1 + M3 - M2 + M6; //at this point , we have calculated the c11..c22 matrices, and now we are going to //put them together and make a unit matrix which would describe our resulting Matrix. for i <- 0 to N/2 for j <- 0 to N/2 MatrixResult[i][j] <- C11[i][j]; MatrixResult[i][j + N / 2] <- C12[i][j]; MatrixResult[i + N / 2][j] <- C21[i][j]; MatrixResult[i + N / 2][j + N / 2] <- C22[i][j];
具体测试代码如下:
// 4-2.矩阵乘法的Strassen算法.cpp : 定义控制台应用程序的入口点。//#include "stdafx.h"#include <iostream>#include <ctime>#include <Windows.h>using namespace std;template<typename T>class Strassen_class{public: void ADD(T** MatrixA, T** MatrixB, T** MatrixResult, int MatrixSize ); void SUB(T** MatrixA, T** MatrixB, T** MatrixResult, int MatrixSize ); void MUL( T** MatrixA, T** MatrixB, T** MatrixResult, int MatrixSize );//朴素算法实现 void FillMatrix( T** MatrixA, T** MatrixB, int length);//A,B矩阵赋值 void PrintMatrix(T **MatrixA,int MatrixSize);//打印矩阵 void Strassen(int N, T **MatrixA, T **MatrixB, T **MatrixC);//Strassen算法实现};template<typename T>void Strassen_class<T>::ADD(T** MatrixA, T** MatrixB, T** MatrixResult, int MatrixSize ){ for ( int i = 0; i < MatrixSize; i++) { for ( int j = 0; j < MatrixSize; j++) { MatrixResult[i][j] = MatrixA[i][j] + MatrixB[i][j]; } }}template<typename T>void Strassen_class<T>::SUB(T** MatrixA, T** MatrixB, T** MatrixResult, int MatrixSize ){ for ( int i = 0; i < MatrixSize; i++) { for ( int j = 0; j < MatrixSize; j++) { MatrixResult[i][j] = MatrixA[i][j] - MatrixB[i][j]; } }}template<typename T>void Strassen_class<T>::MUL( T** MatrixA, T** MatrixB, T** MatrixResult, int MatrixSize ){ for (int i=0;i<MatrixSize ;i++) { for (int j=0;j<MatrixSize ;j++) { MatrixResult[i][j]=0; for (int k=0;k<MatrixSize ;k++) { MatrixResult[i][j]=MatrixResult[i][j]+MatrixA[i][k]*MatrixB[k][j]; } } }}/*c++使用二维数组,申请动态内存方法申请int **A;A = new int *[desired_array_row];for ( int i = 0; i < desired_array_row; i++) A[i] = new int [desired_column_size];释放for ( int i = 0; i < your_array_row; i++) delete [] A[i];delete[] A;*/template<typename T>void Strassen_class<T>::Strassen(int N, T **MatrixA, T **MatrixB, T **MatrixC){ int HalfSize = N/2; int newSize = N/2; if ( N <= 64 ) //分治门槛,小于这个值时不再进行递归计算,而是采用常规矩阵计算方法 { MUL(MatrixA,MatrixB,MatrixC,N); } else { T** A11; T** A12; T** A21; T** A22; T** B11; T** B12; T** B21; T** B22; T** C11; T** C12; T** C21; T** C22; T** M1; T** M2; T** M3; T** M4; T** M5; T** M6; T** M7; T** AResult; T** BResult; //making a 1 diminsional pointer based array. A11 = new T *[newSize]; A12 = new T *[newSize]; A21 = new T *[newSize]; A22 = new T *[newSize]; B11 = new T *[newSize]; B12 = new T *[newSize]; B21 = new T *[newSize]; B22 = new T *[newSize]; C11 = new T *[newSize]; C12 = new T *[newSize]; C21 = new T *[newSize]; C22 = new T *[newSize]; M1 = new T *[newSize]; M2 = new T *[newSize]; M3 = new T *[newSize]; M4 = new T *[newSize]; M5 = new T *[newSize]; M6 = new T *[newSize]; M7 = new T *[newSize]; AResult = new T *[newSize]; BResult = new T *[newSize]; int newLength = newSize; //making that 1 diminsional pointer based array , a 2D pointer based array for ( int i = 0; i < newSize; i++) { A11[i] = new T[newLength]; A12[i] = new T[newLength]; A21[i] = new T[newLength]; A22[i] = new T[newLength]; B11[i] = new T[newLength]; B12[i] = new T[newLength]; B21[i] = new T[newLength]; B22[i] = new T[newLength]; C11[i] = new T[newLength]; C12[i] = new T[newLength]; C21[i] = new T[newLength]; C22[i] = new T[newLength]; M1[i] = new T[newLength]; M2[i] = new T[newLength]; M3[i] = new T[newLength]; M4[i] = new T[newLength]; M5[i] = new T[newLength]; M6[i] = new T[newLength]; M7[i] = new T[newLength]; AResult[i] = new T[newLength]; BResult[i] = new T[newLength]; } //splitting input Matrixes, into 4 submatrices each. for (int i = 0; i < N / 2; i++) { for (int j = 0; j < N / 2; j++) { A11[i][j] = MatrixA[i][j]; A12[i][j] = MatrixA[i][j + N / 2]; A21[i][j] = MatrixA[i + N / 2][j]; A22[i][j] = MatrixA[i + N / 2][j + N / 2]; B11[i][j] = MatrixB[i][j]; B12[i][j] = MatrixB[i][j + N / 2]; B21[i][j] = MatrixB[i + N / 2][j]; B22[i][j] = MatrixB[i + N / 2][j + N / 2]; } } //here we calculate M1..M7 matrices . //M1[][] ADD( A11,A22,AResult, HalfSize); ADD( B11,B22,BResult, HalfSize); //p5=(a+d)*(e+h) Strassen( HalfSize, AResult, BResult, M1 ); //now that we need to multiply this , we use the strassen itself . //M2[][] ADD( A21,A22,AResult, HalfSize); //M2=(A21+A22)B11 p3=(c+d)*e Strassen(HalfSize, AResult, B11, M2); //Mul(AResult,B11,M2); //M3[][] SUB( B12,B22,BResult, HalfSize); //M3=A11(B12-B22) p1=a*(f-h) Strassen(HalfSize, A11, BResult, M3); //Mul(A11,BResult,M3); //M4[][] SUB( B21, B11, BResult, HalfSize); //M4=A22(B21-B11) p4=d*(g-e) Strassen(HalfSize, A22, BResult, M4); //Mul(A22,BResult,M4); //M5[][] ADD( A11, A12, AResult, HalfSize); //M5=(A11+A12)B22 p2=(a+b)*h Strassen(HalfSize, AResult, B22, M5); //Mul(AResult,B22,M5); //M6[][] SUB( A21, A11, AResult, HalfSize); ADD( B11, B12, BResult, HalfSize); //M6=(A21-A11)(B11+B12) p7=(c-a)(e+f) Strassen( HalfSize, AResult, BResult, M6); //Mul(AResult,BResult,M6); //M7[][] SUB(A12, A22, AResult, HalfSize); ADD(B21, B22, BResult, HalfSize); //M7=(A12-A22)(B21+B22) p6=(b-d)*(g+h) Strassen(HalfSize, AResult, BResult, M7); //Mul(AResult,BResult,M7); //C11 = M1 + M4 - M5 + M7; ADD( M1, M4, AResult, HalfSize); SUB( M7, M5, BResult, HalfSize); ADD( AResult, BResult, C11, HalfSize); //C12 = M3 + M5; ADD( M3, M5, C12, HalfSize); //C21 = M2 + M4; ADD( M2, M4, C21, HalfSize); //C22 = M1 + M3 - M2 + M6; ADD( M1, M3, AResult, HalfSize); SUB( M6, M2, BResult, HalfSize); ADD( AResult, BResult, C22, HalfSize); //at this point , we have calculated the c11..c22 matrices, and now we are going to //put them together and make a unit matrix which would describe our resulting Matrix. //组合小矩阵到一个大矩阵 for (int i = 0; i < N/2 ; i++) { for (int j = 0 ; j < N/2 ; j++) { MatrixC[i][j] = C11[i][j]; MatrixC[i][j + N / 2] = C12[i][j]; MatrixC[i + N / 2][j] = C21[i][j]; MatrixC[i + N / 2][j + N / 2] = C22[i][j]; } } // 释放矩阵内存空间 for (int i = 0; i < newLength; i++) { delete[] A11[i];delete[] A12[i];delete[] A21[i]; delete[] A22[i]; delete[] B11[i];delete[] B12[i];delete[] B21[i]; delete[] B22[i]; delete[] C11[i];delete[] C12[i];delete[] C21[i]; delete[] C22[i]; delete[] M1[i];delete[] M2[i];delete[] M3[i];delete[] M4[i]; delete[] M5[i];delete[] M6[i];delete[] M7[i]; delete[] AResult[i];delete[] BResult[i] ; } delete[] A11;delete[] A12;delete[] A21;delete[] A22; delete[] B11;delete[] B12;delete[] B21;delete[] B22; delete[] C11;delete[] C12;delete[] C21;delete[] C22; delete[] M1;delete[] M2;delete[] M3;delete[] M4;delete[] M5; delete[] M6;delete[] M7; delete[] AResult; delete[] BResult ; }//end of else}template<typename T>void Strassen_class<T>::FillMatrix( T** MatrixA, T** MatrixB, int length){ for(int row = 0; row<length; row++) { for(int column = 0; column<length; column++) { MatrixB[row][column] = (MatrixA[row][column] = rand() %5); //matrix2[row][column] = rand() % 2;//ba hazfe in khat 50% afzayeshe soorat khahim dasht } }}template<typename T>void Strassen_class<T>::PrintMatrix(T **MatrixA,int MatrixSize){ cout<<endl; for(int row = 0; row<MatrixSize; row++) { for(int column = 0; column<MatrixSize; column++) { cout<<MatrixA[row][column]<<"\t"; if ((column+1)%((MatrixSize)) == 0) cout<<endl; } } cout<<endl;}int _tmain(int argc, _TCHAR* argv[]){Strassen_class<int> stra;//定义Strassen_class类对象 int MatrixSize = 0; int** MatrixA; //存放矩阵A int** MatrixB; //存放矩阵B int** MatrixC; //存放结果矩阵 clock_t startTime_For_Normal_Multipilication ; clock_t endTime_For_Normal_Multipilication ; clock_t startTime_For_Strassen ; clock_t endTime_For_Strassen ; srand(time(0)); cout<<"\n请输入矩阵大小(必须是2的幂指数值(例如:32,64,512,..): "; cin>>MatrixSize; int N = MatrixSize;//for readiblity. //申请内存 MatrixA = new int *[MatrixSize]; MatrixB = new int *[MatrixSize]; MatrixC = new int *[MatrixSize]; for (int i = 0; i < MatrixSize; i++) { MatrixA[i] = new int [MatrixSize]; MatrixB[i] = new int [MatrixSize]; MatrixC[i] = new int [MatrixSize]; } stra.FillMatrix(MatrixA,MatrixB,MatrixSize); //矩阵赋值 //*******************conventional multiplication test cout<<"朴素矩阵算法开始时钟: "<< (startTime_For_Normal_Multipilication = clock()); stra.MUL(MatrixA,MatrixB,MatrixC,MatrixSize);//朴素矩阵相乘算法 T(n) = O(n^3) cout<<"\n朴素矩阵算法结束时钟: "<< (endTime_For_Normal_Multipilication = clock()); cout<<"\n矩阵运算结果... \n"; stra.PrintMatrix(MatrixC,MatrixSize); //*******************Strassen multiplication test cout<<"\nStrassen算法开始时钟: "<< (startTime_For_Strassen = clock()); stra.Strassen( N, MatrixA, MatrixB, MatrixC ); //strassen矩阵相乘算法 cout<<"\nStrassen算法结束时钟: "<<(endTime_For_Strassen = clock()); cout<<"\n矩阵运算结果... \n"; stra.PrintMatrix(MatrixC,MatrixSize); cout<<"矩阵大小 "<<MatrixSize; cout<<"\n朴素矩阵算法: "<<(endTime_For_Normal_Multipilication - startTime_For_Normal_Multipilication)<<" Clocks.."<<(endTime_For_Normal_Multipilication - startTime_For_Normal_Multipilication)/CLOCKS_PER_SEC<<" Sec"; cout<<"\nStrassen算法:"<<(endTime_For_Strassen - startTime_For_Strassen)<<" Clocks.."<<(endTime_For_Strassen - startTime_For_Strassen)/CLOCKS_PER_SEC<<" Sec\n"; system("Pause");return 0;}运行结果:
性能分析:
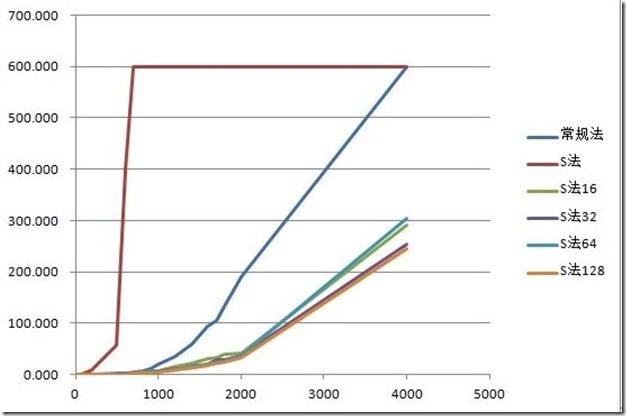
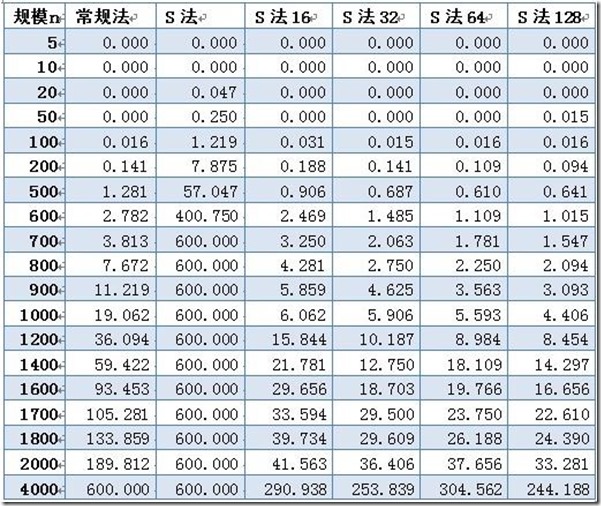
数据取600位上界,即超过10分钟跳出。可以看到使用Strassen算法时,耗时不但没有减少,反而剧烈增多,在n=700时计算时间就无法忍受。仔细研究后发现,采用Strassen算法作递归运算,需要创建大量的动态二维数组,其中分配堆内存空间将占用大量计算时间,从而掩盖了Strassen算法的优势。于是对Strassen算法做出改进,设定一个界限。当n<界限时,使用普通法计算矩阵,而不继续分治递归。
改进后算法优势明显,就算时间大幅下降。之后,针对不同大小的界限进行试验。在初步试验中发现,当数据规模小于1000时,下界S法的差别不大,规模大于1000以后,n取值越大,消耗时间下降。最优的界限值在32~128之间。
因为计算机每次运算时的系统环境不同(CPU占用、内存占用等),所以计算出的时间会有一定浮动。虽然这样,试验结果已经能得出结论Strassen算法比常规法优势明显。使用下界法改进后,在分治效率和动态分配内存间取舍,针对不同的数据规模稍加试验可以得到一个最优的界限。
小结:
1)采用Strassen算法作递归运算,需要创建大量的动态二维数组,其中分配堆内存空间将占用大量计算时间,从而掩盖了Strassen算法的优势
2)于是对Strassen算法做出改进,设定一个界限。当n<界限时,使用普通法计算矩阵,而不继续分治递归。需要合理设置界限,不同环境(硬件配置)下界限不同
3)矩阵乘法一般意义上还是选择的是朴素的方法,只有当矩阵变稠密,而且矩阵的阶数很大时,才会考虑使用Strassen算法。
矩阵乘法的Strassen算法详解
- 矩阵乘法的Strassen算法
- 矩阵乘法的Strassen算法
- STRASSEN算法(矩阵乘法)
- strassen矩阵乘法算法
- 矩阵乘法Strassen算法的伪代码
- 矩阵乘法的Strassen
- strassen算法(矩阵乘法)
- strassen算法优化矩阵乘法
- 算法导论--------------Strassen矩阵乘法
- 矩阵乘法 之 strassen 算法
- Strassen矩阵乘法算法实现
- Strassen算法之矩阵乘法
- 贪心算法-Strassen矩阵乘法
- 算法导论 第四章矩阵乘法的Strassen算法
- 算法导论之四矩阵乘法的Strassen算法
- 用java写的矩阵乘法(Strassen算法)
- 第四章 4.2矩阵乘法的Strassen算法(分治)
- 基于Strassen算法采用分治的矩阵乘法cpp实现
- 网络爬虫
- mongo2.4_point_in_time_recovery
- (交通1)IVMS-8600软件安装手册
- Ubuntu14.04 - Android L50 setup build environment
- 蓝桥杯五1啤酒和饮料
- 矩阵乘法的Strassen算法
- C语言中的存储类型
- request.getParameterNames()步骤
- 20 个实用的 PHP 库(图表、图片、数据等)
- phpmyadmin如何查看索引
- Platform Dependent Compilation 多平台兼容性使用注意事项
- Yui3使用指南一
- 站在巨人的肩上
- Java的native关键字





 ;
;


 ,而Strassen算法复杂度只是
,而Strassen算法复杂度只是 。但随着n的变大,比如当n >> 100时,Strassen算法是比通用矩阵相乘算法变得更有效率。
。但随着n的变大,比如当n >> 100时,Strassen算法是比通用矩阵相乘算法变得更有效率。