POJ 1759(数学递推+二分）

来源：互联网发布：乐知英语的公司在哪编辑：程序博客网时间：2024/04/20 09:32

Garland

Time Limit: 1000MS Memory Limit: 10000KTotal Submissions: 1954 Accepted: 817

Description

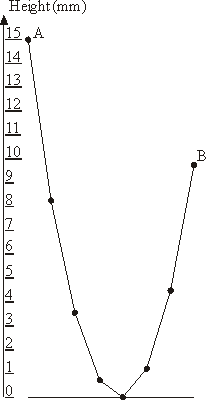The New Year garland consists of N lamps attached to a common wire that hangs down on the ends to which outermost lamps are affixed. The wire sags under the weight of lamp in a particular way: each lamp is hanging at the height that is 1 millimeter lower than the average height of the two adjacent lamps.

The leftmost lamp in hanging at the height of A millimeters above the ground. You have to determine the lowest height B of the rightmost lamp so that no lamp in the garland lies on the ground though some of them may touch the ground.

You shall neglect the lamp's size in this problem. By numbering the lamps with integers from 1 to N and denoting the ith lamp height in millimeters as Hi we derive the following equations:

H1 = A
Hi = (H_i-1 + H_i+1)/2 - 1, for all 1 < i < N
HN = B
Hi >= 0, for all 1 <= i <= N

The sample garland with 8 lamps that is shown on the picture has A = 15 and B = 9.75.

Input

The input file consists of a single line with two numbers N and A separated by a space. N (3 <= N <= 1000) is an integer representing the number of lamps in the garland, A (10 <= A <= 1000) is a real number representing the height of the leftmost lamp above the ground in millimeters.

Output

Write to the output file the single real number B accurate to two digits to the right of the decimal point representing the lowest possible height of the rightmost lamp.

Sample Input

692 532.81

Sample Output

446113.34

首先要用数学知识推导，然后根据推导出来的公式的性质计算，最后用二分暴搜答案

题意

题目背景是在绳上挂灯。。我觉得完全不用鸟这个背景。。。
它表达的核心意思，就是一个数列告诉你首项h1, 项数n，递推式hi = (hi+1 + hi-1 ) / 2 - 1
在保证hi都大于等于0的前提下，让hn最小

思路

这题不难想到可以使用二分，但是二分哪个变量，找到哪样的单调关系需要考虑一下。
首先，通过题目给出的递推式，很容易得到标准的递推形式: hi+1 = 2hi - hi-1 + 2
这样，我们就知道，只要确定了h2，hn肯定就确定了，所以我们二分的变量就是h2了
接下来，我们从递推式入手，来找单调关系
假如递推式为：hi = (hi+1 + hi-1 ) / 2，那会有怎样的结果呢？不难想象，当h2确定时，整个数列就是一个等差数列了，所以数列肯定是单调的。
而如果hi在这个基础上减一呢？不难想象，在hi+1 < hi-1时，hi位于两个数等分位偏hi+1的位置一些，而在hi+1 > hi-1时，hi位于两个数等分位偏hi-1的位置一些。所以在h2 < h1的情况下，整个数列画出的图像一定是先单调递减，但递减幅度越来越小，直至幅度减到足够小，然后递增，并且递增幅度越来越大的过程。
因此，我们的单调关系就是，f(h2): hi是否都大于等于0

Hi = (i-2) * H2 - (i-1) * H1 + (i-1)*(i-2)，也就意味着H2和Hn成正相关，求最小的Hn也就变成了求最小的H2。

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <vector>
#include <queue>
#include <map>
using namespace std;
const int N = 1100;
double h[N];
int judge(double y);
double x;
int n;

int main()
{

while(scanf("%d %lf", &n, &x)!=EOF)
{
double l=0, r=x, mid, ans;
for(int i=0;i<100;i++)
{
mid=(l+r)/2;
if(judge(mid))
{
ans=mid;
r=mid;
}
else
{
l=mid;
}
}
printf("%.2f\n",(n-1)*ans-(n-2)*x+(n-2)*(n-1));
}
return 0;
}

int judge(double y)
{
if(y<0)
{
return 0;
}
h[1]=x, h[2]=y;
for(int i=3;i<=n;i++)
{
h[i]=2*h[i-1]-h[i-2]+2;
if(h[i]<0)
{
return 0;
}
}
return 1;
}

0 0