机器学习算法之SVM(1)结构风险最小化

一、SVM的策略是结构风险最小化
1、几何间隔

线性分类器比如感知机，目的是为了在空间中找出一个超平面，这个超平面使得分类错误率最小。在进行分类的时候，数据集中所有的点都对分界面有影响。

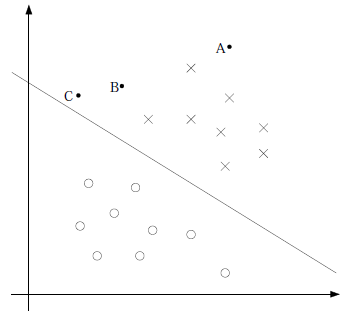
而SVM中使用几何间隔，就是点到分界面的距离γi,试想如果在某一类中离分界面最近的那个点与分界面的距离越大，显然分类的确信度就越大。所以SVM中对分界面有影响的就是那些距离分界面最近的支持向量而不是全部数据点了。

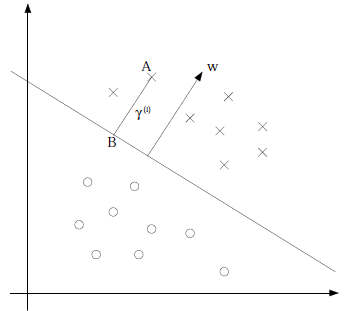
假设分界面为wTx+b=0,点A的坐标为(xi,yi),注意这里的坐标xi是向量，而yi是对应的标签，属于{-1,1}。

由向量的计算得到B点的坐标x=xi−γiw||w||

带入分界面中得：

γi=yi(wTxi+b||w||)

现在定义当wTxi+b>1时为正类，wTxi+b<−1则为负类。

那么我们将距离超平面最近的那个点距离定义为
γmin=1||w||

于是有最优化目标为：

maxw,b1||w||,s.t.yi(wTxi+b)≥1,i=1,..m
现在问题变成了不等式约束的最优化问题。

1||w||中的||w||是向量范数，最大化1||w||等价于最小化12||w||2

于是问题最终变成了二次规划问题：

minw,b12||w||2,s.t.yi(wTxi+b)≥1,i=1,..m

2、结构风险最小化–拉格朗日对偶

假设一个不等式约束问题：

minwf(w),s.t.gi(w)≤0,i=1,..m

由朗格朗日算子得：

L(w,α)=f(w)+∑m1αigi(w)

要求L(w,α)的最小化,因为α≥0，gi(w)≤0,那么可以使α≥0无穷大，使得最终结果无穷小，为了避免这种情况，所以首先先求对α≥0的L(w,α)最大化。

即：L(w)=minwmaxαiL(w,α)

转换成对偶问题求解更方便，在满足KKT条件的情况下：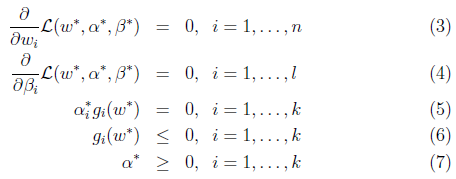

对偶等价：

L(w)=maxαiminwL(w,α)

将SVM的最优化目标和约束条件带入：

L(w,b,α)=12||w||2−∑m1αi(yi(wTxi+b)−1)

式中的第一项，如果||w||是向量的2-范数，那么12||w||2就是12∑m1w2i。

这不就是L-2正则项吗？

第二项则是经验风险啊。

于是我们可以看出，SVM的策略就是结构风险最小化，自带正则项。

二、核函数
1、内积

回到SVM的KKT条件中：

KKT条件：
∂L(w,b,α)∂w=w−∑m1αi(yixi)=0

∂L(w,b,α)∂b=∑m1αi(yi)=0

目标函数：

maxαiminwL(w,b,α)=12||w||2−∑m1αi(yi(wTxi+b)−1)=12wTw−∑m1αiyiwTxi−b∑m1αi(yi)+∑m1αi=12wT∑m1αi(yixi)−wT∑m1αiyixi+∑m1αi=−12wT∑m1αi(yixi)+∑m1αi=−12∑m1αjyj(xj)T∑m1αi(yixi)+∑m1αi=−12∑m1αjαiyjyi(xj)Txi+∑m1αi=∑m1αi–12∑m1αjαiyjyi(xi,xj)

其中(xi,xj)则是向量内积

由于只计算原始特征(xi,xj)内积，就等价与计算映射后特征的内积。

所以可以使用核函数，将在低维的数据映射到高维，从而可以解决非线性分类问题。同时，由于在低维中的计算等价于映射后的结果，又避免了计算量的问题。

2、求解参数αi、w、b

之后的首先求出αi,具体根据SMO算法，

然后根据公式∂L(w,b,α)∂w=w−∑m1αi(yixi)=0，可以求得：

w=∑m1αi(yixi)

最后，根据正负间隔之间的距离相同，可以求得b：

b=maxyi=−1wTxi+minyi=1wTxi2

三、SVM与过拟合

1、虽然SVM的目标函数采用结构风险最小化策略，但是由于SVM在解决非线性分类的时候，引入了核函数，将低维的数据转换到了高维的空间中。显然维数越多，过拟合的风险越大。所以SVM也会过拟合。

2、核函数中的高斯核函数可以将低维数据映射到无穷维中，为什么映射到了无穷维中。

指数函数的泰勒展开式本身就是可以扩展到n维，高斯核只是参数换成了−||x1−x2||22δ2。

3、离群点对于SVM同样会造成过拟合的现象，现在单开一章…..