机器学习笔记——第0篇

文章作者是我的一位大神学长陈雨学长~，征得学长同意后将文章转载到了我的blog上，特在此感谢学长~

代码在学长的github上：
https://github.com/unnamed2/MDL
欢迎猛击

自己实现的机器学习(0):

0.0 前言:

​ 本人辣鸡一个 在努力的学习机器学习算法正在尝试着去理解其中的数学原理.虽然有很多看不懂,不过正是因为这些看不懂,猜想让我记录下来自己的学习历程,日后看着自己一点一点的进步,也许也是个很好玩的过程吧.

前几年Google的AlphaGo战胜李世石的消息,让机器学习(强化学习)的备受关注,大量的机器学习玩家也给出了各式各样的用于机器学习的框架,caffe,TensorFlow,CNTK等等,在这种条件下,自己再去造个轮子似乎没什么卵用,但是说,在这造的轮子能帮助人们更好的理解其数学原理,也能算是有点用的轮子吧:smile:

​ 由于各种原因,我将只实现有监督的学习算法.

0.1 说明:

0.1.0:使用的语言:

事实证明 , 现在大量的算法都是基于python语言的实现,毕竟python语法相对简单,扩展库强大,等等

但是我偏偏要使用C++实现他们,可能是我脑残吧.

0.1.1使用的Library:

线性代数的运算库:据我所知,这个学习算法可能需要大量的线性代数的运算,例如向量,矩阵和一些在他们上面的操作等等. 采用MKL来完成(我使用的是微软为CNTK定制的版本,因为这是现成的:smile:),我自己将其简单的包装了一下来避开因为不熟悉而难理解的函数调用,当然不喜欢MKL也可以自己用其他方法实现以下用于计算的Matrix类的成员,即可.和线性代数常用的矩阵不同,线性代数中的矩阵的行矩阵,我所实现的是列矩阵

图形处理:如果学习机器学习却不尝试着处理图片的话那就太可惜了啊哈哈 将采用OpenCV进行图片加载和预处理.

不过因为自己实现的算法,效率上一定超越不了现有的框架,而且会被扣很多圈,再加上计算量过大,所以将不会分析处理过大的图片.

0.1.2数据集:

MINST :　60000个手写数字的图片(28x28的灰度图)，　将会玩这个直到玩坏为止．

CIFAR神奇的Cifar数据集各种类别的图片(32x32的彩色图片)

0.1.3 我的代码

基础线性代数部分直接复制的微软大大的CNTK里面的CPUMatrix代码.请在遵守CNTK开源协议的前提下使用该源码.如若觉得我写的速度比较慢,也欢迎自己实现该数学库.

在写这玩意的期间我会慢慢搭建起来一个简单的弱鸡的深度学习框架,欢迎各位大大来看看并提出意见.

代码在这,欢迎阅读:smile:.

0.2 梯度下降

机器学习的过程，实际上就是寻找一个函数的最小值的过程。

梯度下降算法可以说是整个机器学习的基础数学理论,非常重要的理论.

梯度下降是 在数学的意义上 是用来寻找函数最小值,是无约束最优化求解的计算方法之一;

在机器学习中我们将会设计一个函数 并计算和标签数据的误差 我们用梯度下降方法使得误差最小.

我知道可能正常来讲见到数学的式子可能就发自内心的拒绝,所以先看看结果可能有好处:

在xk处f(xk)沿着f的梯度方向即(∇f=(∂f∂x1,∂f∂x2,∂f∂x3,...))方向的反方向下降最快.

0.2.1 二维情况

对于在(x0,y0)处f(x,y)沿着(−∂f∂x,−∂f∂y)的方向上下降速度最快.

证明:　由全微分方程

limΔx→0,Δy→0(f(x0+Δx,y0+Δy)−f(x0,y0))=limΔx→0,Δy→0(∂f∂x0Δx+∂f∂y0Δy+o(ε))(ε=Δx2+Δy2−−−−−−−−−√)

=limε→0(ε⟨∇f,p⟩)

(其中∇f是f在(x0,y0)的梯度,p是(Δx,Δy)的方向向量,即εp=(x0,y0))

⟨a,b⟩表示点乘也叫内积.

显然在∇f,p的夹角为180度的时候,内积的值最小,为−∥∇f∥.

0.2.2 高纬度的情况:

对于任意维度,limε→0(f(x+εp)−f(x))=limε→0(ε⟨∇f,p⟩)仍成立,所以该结论对于高纬度仍然成立.

0.2.3几何上的梯度下降:

想象一个小球放在一个不规则的曲面上: 小球将会沿着下降最快的方向下降:

​

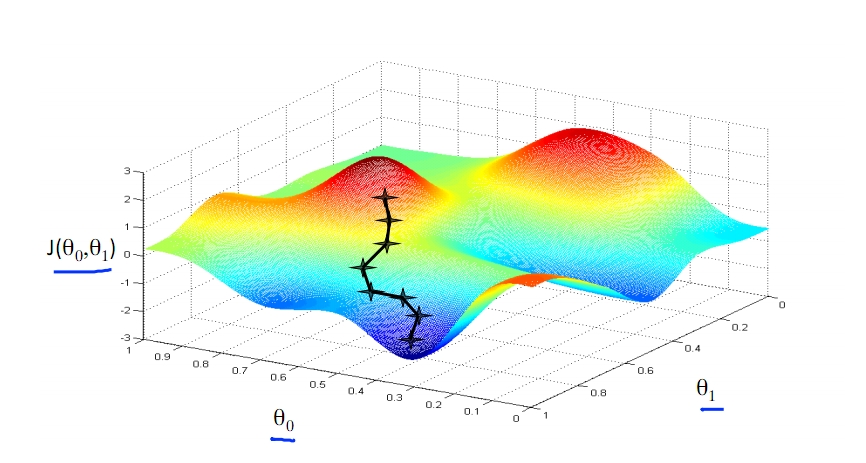
不过,并不能保证一定能找到函数的最小值:

为了克服梯度下降容易陷入函数的局部最小值的缺点，在梯度下降方法的基础上，还有很多改进的寻求最小值的算法，例如随机梯度下降算法(Stochastic Gradient Descent,SGD),动量梯度下降算法（Momentum SGD）等等。之后我们会使用小批量的SGD算法。

梯度下降算法是在一阶偏导下的计算函数最小值的方法，同时还有基于二阶偏导的Hesse矩阵的方法，拟牛顿法等等，这些方法的下降速度将会超过梯度下降算法，但是由于超高的计算量让正常的计算机无法承受。 例如想要计算一个只有10000个参数的Hesse矩阵，那么这个矩阵就是一个10000x10000的矩阵，大约消耗400MB的内存空间，实际上我们马上会看到，我们使用的参数数量将会远远的超过这个值， 总之，Hesse方法和类似的拟牛顿法都过于消耗时间和空间，目前的硬件还无法承受。所以我们将不会使用这种方法。

0.2.4 利用梯度下降求解函数最小值

用一个简单的抛物面函数来做例子:

​

f(x,y)=(x−1)2+(y−2)2

显然,这个函数在(1,2)处有最小值0.下面我们用梯度下降的搜索算法来求取这个最小值.

1.在什么都不知道的情况下 随便选取一个初始位置 比如v0=(5,7);

2.求得在该点的梯度值∇f=(∂f∂x,∂f∂y)=(2˙(x−1),2˙(y−2))=(8,12)

3.选取一个步长, 这个值通常介于(0,1)之间,这里我们选0.1;

4.计算下一个位点v1=(5,7)−(8,12)∗0.1=(4.2,5.8)

5.对新计算的位点重复第2部,直到梯度无限接近于0或者等于0.

这里我们能够得到一个搜索序列:

v0=(5,7),v1=(4.2,5.8),v3=(3.56,4.84),v4=(3.048,4.072),.....

经过一阵迭代之后 会发下我们选取的搜索点的函数值越来越小,最终会收敛在最小值附近.