Minimax算法及其剪枝优化Alpha-beta
来源:互联网 发布:吉林大学网络本科 编辑:程序博客网 时间:2024/05/18 12:00
转载自http://blog.codinglabs.org/articles/2048-ai-analysis.html!!!!!
Minimax
下面先介绍不带剪枝的Minimax。首先本文将通过一个简单的例子说明Minimax算法的思路和决策方式。
问题
现在考虑这样一个游戏:有三个盘子A、B和C,每个盘子分别放有三张纸币。A放的是1、20、50;B放的是5、10、100;C放的是1、5、20。单位均为“元”。有甲、乙两人,两人均对三个盘子和上面放置的纸币有可以任意查看。游戏分三步:
甲从三个盘子中选取一个。
乙从甲选取的盘子中拿出两张纸币交给甲。
甲从乙所给的两张纸币中选取一张,拿走。
其中甲的目标是最后拿到的纸币面值尽量大,乙的目标是让甲最后拿到的纸币面值尽量小。
下面用Minimax算法解决这个问题。
基本思路
一般解决博弈类问题的自然想法是将格局组织成一棵树,树的每一个节点表示一种格局,而父子关系表示由父格局经过一步可以到达子格局。Minimax也不例外,它通过对以当前格局为根的格局树搜索来确定下一步的选择。而一切格局树搜索算法的核心都是对每个格局价值的评价。Minimax算法基于以下朴素思想确定格局价值:
Minimax是一种悲观算法,即假设对手每一步都会将我方引入从当前看理论上价值最小的格局方向,即对手具有完美决策能力。因此我方的策略应该是选择那些对方所能达到的让我方最差情况中最好的,也就是让对方在完美决策下所对我造成的损失最小。
Minimax不找理论最优解,因为理论最优解往往依赖于对手是否足够愚蠢,Minimax中我方完全掌握主动,如果对方每一步决策都是完美的,则我方可以达到预计的最小损失格局,如果对方没有走出完美决策,则我方可能达到比预计的最悲观情况更好的结局。总之我方就是要在最坏情况中选择最好的。
上面的表述有些抽象,下面看具体示例。
解题
下图是上述示例问题的格局树:
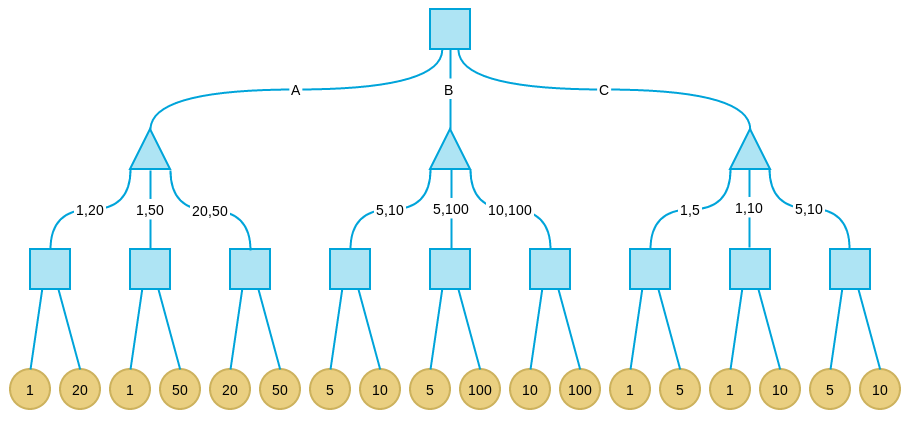
注意,由于示例问题格局数非常少,我们可以给出完整的格局树。这种情况下我可以找到Minimax算法的全局最优解。而真实情况中,格局树非常庞大,即使是计算机也不可能给出完整的树,因此我们往往只搜索一定深度,这时只能找到局部最优解。
我们从甲的角度考虑。其中正方形节点表示轮到我方(甲),而三角形表示轮到对方(乙)。经过三轮对弈后(我方-对方-我方),将进入终局。黄色叶结点表示所有可能的结局。从甲方看,由于最终的收益可以通过纸币的面值评价,我们自然可以用结局中甲方拿到的纸币面值表示终格局的价值。
下面考虑倒数第二层节点,在这些节点上,轮到我方选择,所以我们应该引入可选择的最大价值格局,因此每个节点的价值为其子节点的最大值:
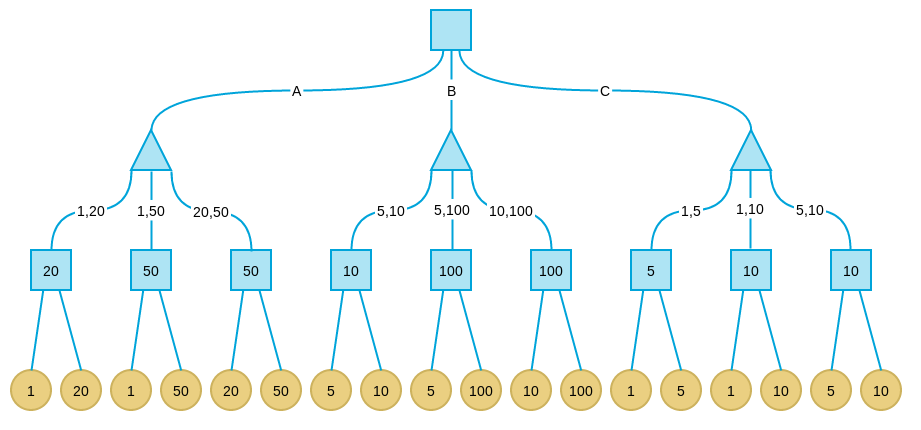
这些轮到我方的节点叫做max节点,max节点的值是其子节点最大值。
倒数第三层轮到对方选择,假设对方会尽力将局势引入让我方价值最小的格局,因此这些节点的价值取决于子节点的最小值。这些轮到对方的节点叫做min节点。
最后,根节点是max节点,因此价值取决于叶子节点的最大值。最终完整赋值的格局树如下:
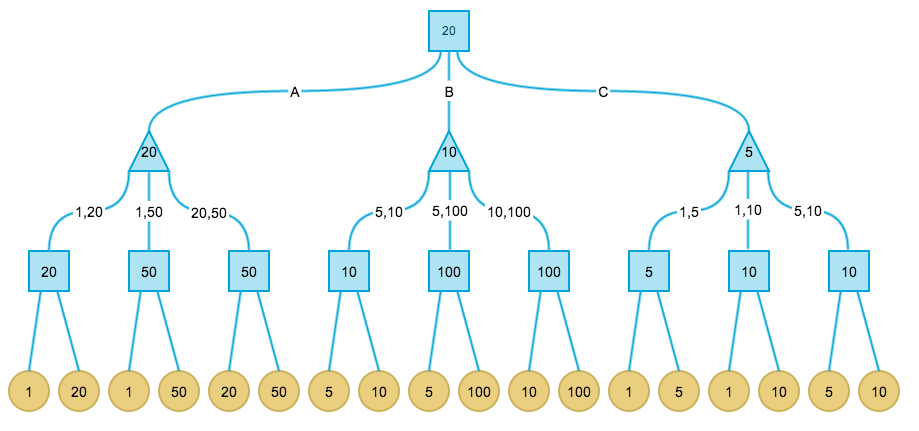
总结一下Minimax算法的步骤:
首先确定最大搜索深度D,D可能达到终局,也可能是一个中间格局。
在最大深度为D的格局树叶子节点上,使用预定义的价值评价函数对叶子节点价值进行评价。
自底向上为非叶子节点赋值。其中max节点取子节点最大值,min节点取子节点最小值。
每次轮到我方时(此时必处在格局树的某个max节点),选择价值等于此max节点价值的那个子节点路径。
在上面的例子中,根节点的价值为20,表示如果对方每一步都完美决策,则我方按照上述算法可最终拿到20元,这是我方在Minimax算法下最好的决策。格局转换路径如下图红色路径所示:
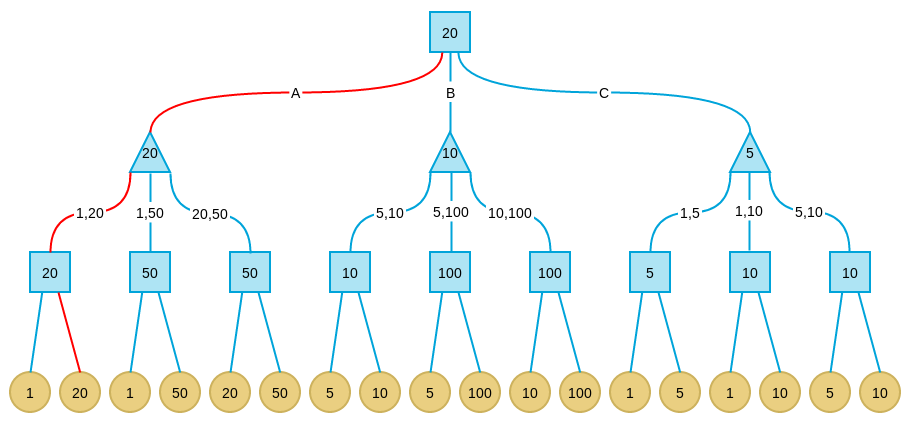
对于真实问题中的Minimax,再次强调几点:
真实问题一般无法构造出完整的格局树,所以需要确定一个最大深度D,每次最多从当前格局向下计算D层。
因为上述原因,Minimax一般是寻找一个局部最优解而不是全局最优解,搜索深度越大越可能找到更好的解,但计算耗时会呈指数级膨胀。
也是因为无法一次构造出完整的格局树,所以真实问题中Minimax一般是边对弈边计算局部格局树,而不是只计算一次,但已计算的中间结果可以缓存。
Alpha-beta剪枝
简单的Minimax算法有一个很大的问题就是计算复杂性。由于所需搜索的节点数随最大深度呈指数膨胀,而算法的效果往往和深度相关,因此这极大限制了算法的效果。
Alpha-beta剪枝是对Minimax的补充和改进。采用Alpha-beta剪枝后,我们可不必构造和搜索最大深度D内的所有节点,在构造过程中,如果发现当前格局再往下不能找到更好的解,我们就停止在这个格局及以下的搜索,也就是剪枝。
Alpha-beta基于这样一种朴素的思想:时时刻刻记得当前已经知道的最好选择,如果从当前格局搜索下去,不可能找到比已知最优解更好的解,则停止这个格局分支的搜索(剪枝),回溯到父节点继续搜索。
Alpha-beta算法可以看成变种的Minimax,基本方法是从根节点开始采用深度优先的方式构造格局树,在构造每个节点时,都会读取此节点的alpha和beta两个值,其中alpha表示搜索到当前节点时已知的最好选择的下界,而beta表示从这个节点往下搜索最坏结局的上界。由于我们假设对手会将局势引入最坏结局之一,因此当beta小于alpha时,表示从此处开始不论最终结局是哪一个,其上限价值也要低于已知的最优解,也就是说已经不可能此处向下找到更好的解,所以就会剪枝。
下面同样以上述示例介绍Alpha-beta剪枝算法的工作原理。我们从根节点开始,详述使用Alpha-beta的每一个步骤:
根节点的alpha和beta分别被初始化为\(-\infty\),和\(+\infty\)。
深度优先搜索第一个孩子,不是叶子节点,所以alpha和beta继承自父节点,分别为\(-\infty\),和\(+\infty\)
搜索第三层的第一个孩子,同上。
搜索第四层,到达叶子节点,采用评价函数得到此节点的评价值为1。
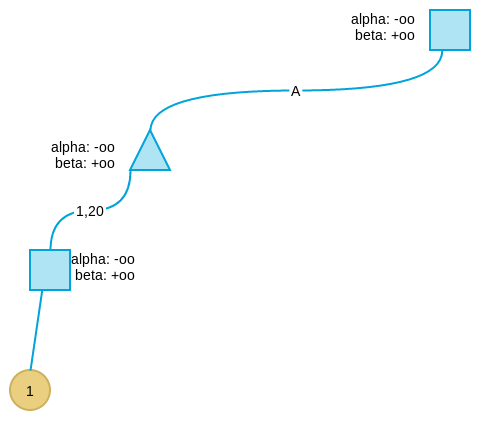
此叶节点的父节点为max节点,因此更新其alpha值为1,表示此节点取值的下界为1。
再看另外一个子节点,值为20,大于当前alpha值,因此将alpha值更新为20。
此时第三层最左节点所有子树搜索完毕,作为max节点,更新其真实值为当前alpha值:20。
由于其父节点(第二层最左节点)为min节点,因此更新其父节点beta值为20,表示这个节点取值最多为20。
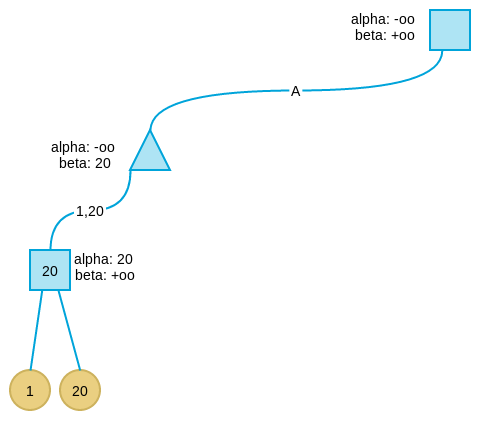
搜索第二层最左节点的第二个孩子及其子树,按上述逻辑,得到值为50(注意第二层最左节点的beta值要传递给孩子)。由于50大于20,不更新min节点的beta值。
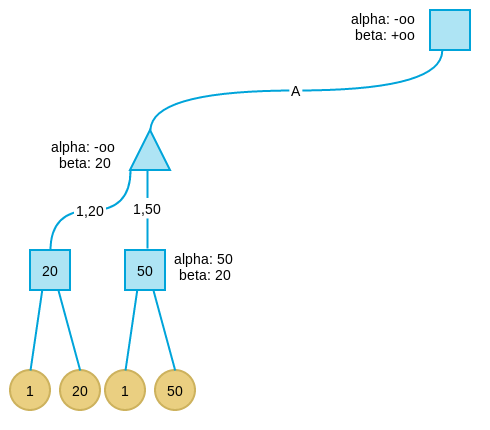
搜索第二层最左节点的第三个孩子。当看完第一个叶子节点后,发现第三个孩子的alpha=beta,此时表示这个节点下不会再有更好解,于是剪枝。
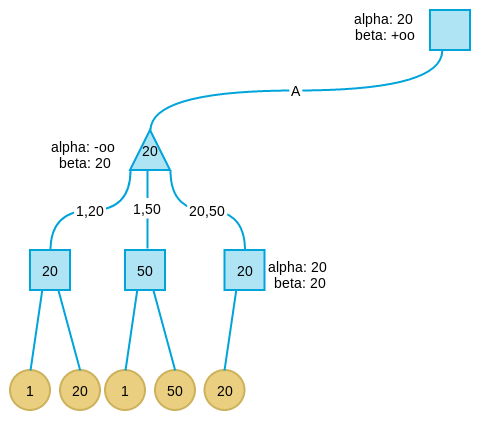
继续搜索B分支,当搜索完B分支的第一个孩子后,发现此时B分支的alpha为20,beta为10。这表示B分支节点的最大取值不会超过10,而我们已经在A分支取到20,此时满足alpha大于等于beta的剪枝条件,因此将B剪枝。并将B分支的节点值设为10,注意,这个10不一定是这个节点的真实值,而只是上线,B节点的真实值可能是5,可能是1,可能是任何小于10的值。但是已经无所谓了,反正我们知道这个分支不会好过A分支,因此可以放弃了。
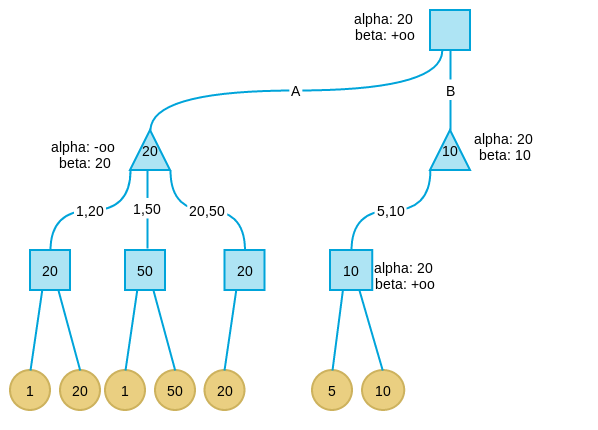
在C分支搜索时遇到了与B分支相同的情况。因此讲C分支剪枝。
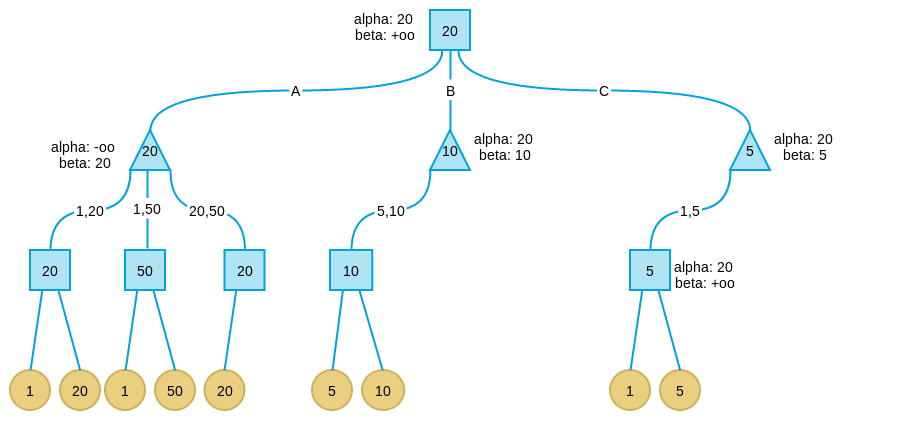
此时搜索全部完毕,而我们也得到了这一步的策略:应该走A分支。
可以看到相比普通Minimax要搜索18个叶子节点相比,这里只搜索了9个。采用Alpha-beta剪枝,可以在相同时间内加大Minimax的搜索深度,因此可以获得更好的效果。并且Alpha-beta的解和普通Minimax的解是一致的。
- Minimax算法及其剪枝优化Alpha-beta
- Alpha-Beta 剪枝算法
- alpha beta 剪枝算法
- Alpha-Beta剪枝算法
- Alpha-beta剪枝算法
- Alpha-Beta剪枝算法(Alpha Beta Pruning)
- AI基础中的Minimax及Alpha-beta算法
- Alpha-beta剪枝算法实例分析
- Alpha-beta剪枝算法实例分析
- 五子棋AI算法-Alpha Beta剪枝
- 极大极小树的剪枝算法1 alpha-beta剪枝
- alpha-beta剪枝搜索
- 例析Alpha-Beta剪枝
- alpha-beta剪枝
- 例析Alpha-Beta剪枝
- Alpha-beta剪枝-井字棋
- Alpha-Beta剪枝(Alpha Beta Pruning)
- 五子棋AI算法第三篇-Alpha Beta剪枝
- Android-Universal-Image-Loader 图片异步加载类库的使用(超详细配置)
- Maven学习总结(3)——使用Maven构建项目
- IDEA 格式化代码快捷键冲突解决
- java card平台详解
- Win32消息机制
- Minimax算法及其剪枝优化Alpha-beta
- elasticsearch笔记_相关度控制(八)
- shiro获取当前用户信息不对称的解决办法
- 关于Java的File.separator
- 代码本地测试正常,上传至服务器报错
- iOS-设置显示时间-NSDateFormatter
- IntelliJ IDEA单元测试入门
- FTP的简介
- 事件委托的定义


