DistMesh

DistMesh - A Simple Mesh Generator in MATLAB

News (Mar 11, 2012)

I have not been maintaining/updating the distmesh code since I wrote it, butby popular request I have now posted a new version. The main differences andnew features are:

• New 3-D surface mesh generator distmeshsurface.m, type "help distmeshsurface" to see some examples.
• Support for general implicit functions in distmesh2d and distmeshsurface. This means e.g. that an ellipse can be represented by the simple expression phi(x,y)=(x/a)^2+(y/b)^2-1, even if this is not a signed distance function.
• Robustness improvements in distmesh2d, including removal of duplicated fix points, density control, and a final mesh cleanup.
• Recompiled C-functions for 32/64-bit Windows, 64-bit Mac OS X, and 64-bit linux.
• More examples and more consistent size functions in the examples, including a NACA0012 airfoil mesh. Type "help distmesh2d", run the demo "meshdemo2d", or just look at the examples further down on this page.

Description

DistMesh is a simple MATLAB code for generation of unstructuredtriangular and tetrahedral meshes. It was developed byPer-Olof Persson (nowatUC Berkeley) and Gilbert Strang in the Department of Mathematics atMIT. A detailed description of theprogram is provided in our SIAM Review paper, see documentation below.

One reason that the code is short and simple is that the geometries arespecified bySigned Distance Functions. These give the shortestdistance from any point in space to the boundary of the domain. The signis negative inside the region and positive outside. A simple example isthe unit circle in 2-D, which has the distance functiond=r-1,where r is the distance from the origin. For more complicatedgeometries the distance function can be computed by interpolation betweenvalues on a grid, a common representation for level set methods.

For the actual mesh generation, DistMesh uses the Delaunay triangulationroutine in MATLAB and tries to optimize the node locations by a force-basedsmoothing procedure. The topology is regularly updated by Delaunay.The boundary points are only allowed to move tangentially to the boundaryby projections using the distance function.This iterative procedure typically results in very well-shaped meshes.

Our aim with this code is simplicity, so that everyone canunderstand the code and modify it according to their needs. The codeis not entirely robust (that is, it might not terminate and return awell-shaped mesh), and it is relatively slow. However, our currentresearch shows that these issues can be resolved in an optimized C++code, and we believe our simple MATLAB code is important fordemonstration of the underlying principles.

To use the code, simply download it from below and run it from MATLAB.For a quick demonstration, type "meshdemo2d" or "meshdemond".For more details see the documentation.

Download

Download the archive below and unpack. Add this directory to your MATLABpath, or make it the current directory. The code contains some C++ files,and binaries for 32/64-bit Windows, 64-bit Mac OS X, and 64-bit linux areprovided, as well as the source code.

• distmesh.zip Current version 1.1 - complete package (ZIP archive)
• distmesh_v10.zip Original version 1.0 - complete package (ZIP archive)

DistMesh is distributed under the GNU GPL;see the License and Copyright notice for more information.

Documentation

• P.-O. Persson, G. Strang, A Simple Mesh Generator in MATLAB.
  SIAM Review, Volume 46 (2), pp. 329-345, June 2004 (PDF)
• P.-O. Persson, Mesh Generation for Implicit Geometries.
  Ph.D. thesis, Department of Mathematics, MIT, Dec 2004 (PDF)
• Function reference

Gallery

• Images
• Movies
• Interactive Java Applets

• Applications and Moving Meshes

Examples

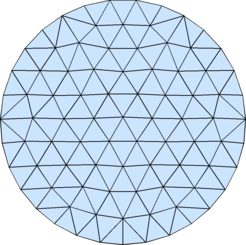
% Example: (Uniform Mesh on Unit Circle)    fd=@(p) sqrt(sum(p.^2,2))-1;    [p,t]=distmesh2d(fd,@huniform,0.2,[-1,-1;1,1],[]);

% Example: (Rectangle with circular hole, refined at circle boundary)    fd=@(p) ddiff(drectangle(p,-1,1,-1,1),dcircle(p,0,0,0.5));    fh=@(p) 0.05+0.3*dcircle(p,0,0,0.5);    [p,t]=distmesh2d(fd,fh,0.05,[-1,-1;1,1],[-1,-1;-1,1;1,-1;1,1]);

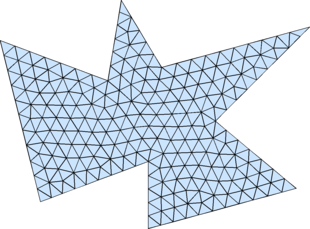
% Example: (Polygon)    pv=[-0.4 -0.5;0.4 -0.2;0.4 -0.7;1.5 -0.4;0.9 0.1;        1.6 0.8;0.5 0.5;0.2 1;0.1 0.4;-0.7 0.7;-0.4 -0.5];    [p,t]=distmesh2d(@dpoly,@huniform,0.1,[-1,-1; 2,1],pv,pv);

% Example: (Ellipse)    fd=@(p) p(:,1).^2/2^2+p(:,2).^2/1^2-1;    [p,t]=distmesh2d(fd,@huniform,0.2,[-2,-1;2,1],[]);

% Example: (Square, with size function point and line sources)    fd=@(p) drectangle(p,0,1,0,1);    fh=@(p) min(min(0.01+0.3*abs(dcircle(p,0,0,0)), ...                 0.025+0.3*abs(dpoly(p,[0.3,0.7; 0.7,0.5]))),0.15);    [p,t]=distmesh2d(fd,fh,0.01,[0,0;1,1],[0,0;1,0;0,1;1,1]);

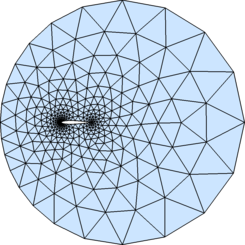
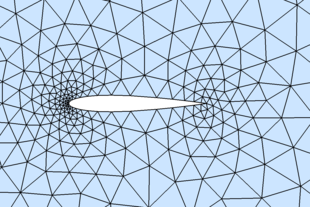
% Example: (NACA0012 airfoil)    hlead=0.01; htrail=0.04; hmax=2; circx=2; circr=4;    a=.12/.2*[0.2969,-0.1260,-0.3516,0.2843,-0.1036];    fd=@(p) ddiff(dcircle(p,circx,0,circr),(abs(p(:,2))-polyval([a(5:-1:2),0],p(:,1))).^2-a(1)^2*p(:,1));    fh=@(p) min(min(hlead+0.3*dcircle(p,0,0,0),htrail+0.3*dcircle(p,1,0,0)),hmax);    fixx=1-htrail*cumsum(1.3.^(0:4)');    fixy=a(1)*sqrt(fixx)+polyval([a(5:-1:2),0],fixx);    fix=[[circx+[-1,1,0,0]*circr; 0,0,circr*[-1,1]]'; 0,0; 1,0; fixx,fixy; fixx,-fixy];    box=[circx-circr,-circr; circx+circr,circr];    h0=min([hlead,htrail,hmax]);    [p,t]=distmesh2d(fd,fh,h0,box,fix);

% Example: (Uniform Mesh on Unit Sphere)    fd=@(p) dsphere(p,0,0,0,1);    [p,t]=distmeshsurface(fd,@huniform,0.2,1.1*[-1,-1,-1;1,1,1]);

% Example: (Graded Mesh on Unit Sphere)    fd=@(p) dsphere(p,0,0,0,1);    fh=@(p) 0.05+0.5*dsphere(p,0,0,1,0);    [p,t]=distmeshsurface(fd,fh,0.15,1.1*[-1,-1,-1;1,1,1]);

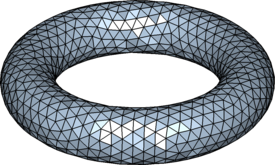
% Example: (Uniform Mesh on Torus)    fd=@(p) (sum(p.^2,2)+.8^2-.2^2).^2-4*.8^2*(p(:,1).^2+p(:,2).^2);    [p,t]=distmeshsurface(fd,@huniform,0.1,[-1.1,-1.1,-.25;1.1,1.1,.25]);

% Example: (Uniform Mesh on Ellipsoid)    fd=@(p) p(:,1).^2/4+p(:,2).^2/1+p(:,3).^2/1.5^2-1;    [p,t]=distmeshsurface(fd,@huniform,0.2,[-2.1,-1.1,-1.6; 2.1,1.1,1.6]);

---

Per-Olof Persson
Department of Mathematics, UC Berkeley
[e-mail]