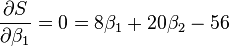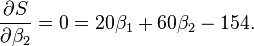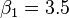最小二乘法
来源:互联网 发布:联系打字软件 编辑:程序博客网 时间:2024/06/05 20:30
最小二乘法(又称最小平方法)是一种数学优化技术。它通过最小化误差的平方和寻找数据的最佳函数匹配。
利用最小二乘法可以简便地求得未知的数据,并使得这些求得的数据与实际数据之间误差的平方和为最小。
最小二乘法还可用于曲线拟合。
其他一些优化问题也可通过最小化能量或最大化熵用最小二乘法来表达。
示例[编辑]
某次实验得到了四个数据点  :
: 、
、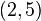 、
、 、
、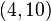 (右图中红色的点)。我们希望找出一条和这四个点最匹配的直线
(右图中红色的点)。我们希望找出一条和这四个点最匹配的直线 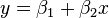 ,即找出在某种“最佳情况”下能够大致符合如下超定线性方程组的
,即找出在某种“最佳情况”下能够大致符合如下超定线性方程组的  和
和 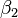 :
:
最小二乘法采用的手段是尽量使得等号两边的方差最小,也就是找出这个函数的最小值:
最小值可以通过对 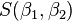 分别求
分别求  和
和 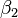 的偏导数,然后使它们等于零得到。
的偏导数,然后使它们等于零得到。
如此就得到了一个只有两个未知数的方程组,很容易就可以解出:
也就是说直线  是最佳的。
是最佳的。
阅读全文
0 0
- 最小二乘法
- 最小二乘法
- 最小二乘法
- 最小二乘法
- 最小二乘法
- 最小二乘法
- 最小二乘法
- 最小二乘法
- 最小二乘法
- 最小二乘法
- 最小二乘法
- 最小二乘法
- 最小二乘法
- 最小二乘法
- 最小二乘法
- 最小二乘法
- 最小二乘法
- 最小二乘法
- 支付宝通知页面notify_url、返回页面return_url
- 机器学习性能改善备忘单:32个帮你做出更好预测模型的技巧和窍门
- 电磁干扰的主要来源
- Andorid Tv 开发 基础以及 应用安装上打不开,没图标以及遥控器选择的问题
- Java设计模式-抽象工厂模式
- 最小二乘法
- freemarker 中list循环 时间处理
- UINavigationController注意事项
- 二、关于Apache的版本
- 从零开始:微信小程序新手入门宝典(正在更新)
- log4net基础应用,实现项目日志文件开启!
- 【iOS】导航栏和工具栏
- git 命令
- JAVA如何把一个float四舍五入到小数点后2位,4位,或者其它指定位数.

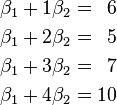
![\begin{align}S(\beta_1, \beta_2) = &\left[6-(\beta_1+1\beta_2)\right]^2+\left[5-(\beta_1+2\beta_2) \right]^2 \\&+\left[7-(\beta_1 + 3\beta_2)\right]^2+\left[10-(\beta_1 + 4\beta_2)\right]^2.\\\end{align}](http://upload.wikimedia.org/math/a/2/1/a21abd8e36caa43fcfd6dedbbaac4af1.png)