斐波那契数列

来源：互联网发布：性格被动知乎编辑：程序博客网时间：2024/06/05 07:15

原文地址：http://dudu.zhihu.com/story/7756498

一、起源和定义

斐波那契数列最早被提出是印度数学家Gopala，他在研究箱子包装物件长度恰好为1和2时的方法数时首先描述了这个数列。也就是这个问题：

有n个台阶，你每次只能跨一阶或两阶，上楼有几种方法？

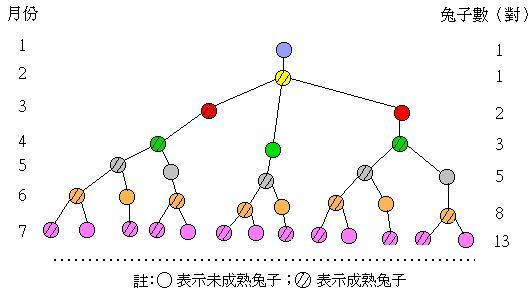
而最早研究这个数列的当然就是斐波那契（Leonardo Fibonacci）了，他当时是为了描述如下情况的兔子生长数目：

第一个月初有一对刚诞生的兔子
第二个月之后（第三个月初）它们可以生育
每月每对可生育的兔子会诞生下一对新兔子
兔子永不死去

这个数列出自他赫赫有名的大作《计算之书》（没有维基词条，坑），后来就被广泛的应用于各种场合了。这个数列是这么定义的：

The On-Line Encyclopedia of Integer Sequences® (OEIS®)序号为A000045 - OEIS

（注意，并非满足第三条的都是斐波那契数列，卢卡斯数列（A000032 - OEIS）也满足这一特点，但初始项定义不同）

二、求解方法

讲完了定义，再来说一说如何求对应的项。斐波那契数列是编程书中讲递归必提的，因为它是按照递归定义的。所以我们就从递归开始讲起。

1.递归求解

int Fib(int n){return n < 2 ? 1 : (Fib(n-1) + Fib(n-2));}

这是编程最方便的解法，当然，也是效率最低的解法，原因是会出现大量的重复计算。为了避免这种情况，可以采用递推的方式。

2.递推求解

int Fib[1000];Fib[0] = 0;Fib[1] = 1;for(int i = 2;i < 1000;i++) Fib[i] = Fib[i-1] + Fib[i-2];

递推的方法可以在O(n)的时间内求出Fib(n)的值。但是这实际还是不够好，因为当n很大时这个算法还是无能为力的。接下来就要来讲一个有意思的东西：矩阵。

3.矩阵递推关系

学过代数的人可以看出，下面这个式子是成立的：
$\begin{bmatrix}Fib(n+1) \\Fib(n)\end {bmatrix}=\begin{bmatrix}1&1 \\1&0\end{bmatrix}\begin{bmatrix}Fib(n) \\Fib(n-1)\end{bmatrix}$
不停地利用这个式子迭代右边的列向量，会得到下面的式子：
$\begin{bmatrix}Fib(n+1) \\Fib(n)\end {bmatrix}=\begin{bmatrix}1&1 \\1&0\end{bmatrix}^{n}\begin{bmatrix}Fib(1) \\Fib(0)\end{bmatrix}$
这样，问题就转化为如何计算这个矩阵的n次方了，可以采用快速幂的方法。快速幂_百度百科是利用结合律快速计算幂次的方法。比如我要计算 $2^{20}$ ，我们知道 $2^{20} = 2^{16} * 2^{4}$ ，而 $2^{2}$ 可以通过 $2^{1} \times 2^{1}$ 来计算， $2^{4}$ 而可以通过 $2^{2}\times 2^{2}$ 计算，以此类推。通过这种方法，可以在O（lbn）的时间里计算出一个数的n次幂。快速幂的代码如下：

int Qpow(int a,int n){    int ans = 1;    while(n)    {        if(n&1) ans *= a;        a *= a;        n >>= 1;    }    return ans;}

将上述代码中的整型变量a变成矩阵，数的乘法变成矩阵乘法，就是矩阵快速幂了。比如用矩阵快速幂计算斐波那契数列：

#include <cstdio>#include <iostream>using namespace std;const int MOD = 10000;struct matrix//定义矩阵结构体{    int m[2][2];}ans, base;matrix multi(matrix a, matrix b)//定义矩阵乘法{    matrix tmp;    for(int i = 0; i < 2; ++i)    {        for(int j = 0; j < 2; ++j)        {            tmp.m[i][j] = 0;            for(int k = 0; k < 2; ++k)                tmp.m[i][j] = (tmp.m[i][j] + a.m[i][k] * b.m[k][j]) % MOD;        }    }    return tmp;}int fast_mod(int n)  // 求矩阵 base 的  n 次幂 {    base.m[0][0] = base.m[0][1] = base.m[1][0] = 1;    base.m[1][1] = 0;    ans.m[0][0] = ans.m[1][1] = 1;  // ans 初始化为单位矩阵     ans.m[0][1] = ans.m[1][0] = 0;    while(n)    {        if(n & 1)  //实现 ans *= t; 其中要先把 ans赋值给 tmp，然后用 ans = tmp * t             ans = multi(ans, base);        base = multi(base, base);        n >>= 1;    }    return ans.m[0][1];}int main(){    int n;    while(scanf("%d", &n) && n != -1)    {           printf("%d\n", fast_mod(n));    }    return 0;}

4.通项公式

无论如何，对于一个数列，我们都是希望可以建立 $F(n)$ 与n的关系，也就是通项公式，而用不同方法去求解通项公式也是很有意思的。

（1）构造等比数列

设 $f(n) + \alpha f(n-1) = \beta [f(n-1) + \alpha f(n-2)]$ ,
化简得 $f(n)=(\beta -\alpha )f(n-1)+\alpha \beta f(n-2)$ ,
比较系数得 $\beta -\alpha =1,\alpha \beta =1$ ，
解得 $\alpha =\frac{\sqrt{5}-1 }{2}$ ， $\beta =\frac{\sqrt{5}+1 }{2}$
由于 $f(n+1)+\alpha f(n)=[f(2)+\alpha f(1)]\beta ^{n-1} =\beta ^{n}$
故有 $\frac{f(n+1)}{\beta ^{n+1}} +\frac{\alpha}{\beta } \frac{f(n)}{\beta ^{n} } =\frac{1}{\beta }$ ，设 $g(n)=\frac{f(n)}{\beta ^{n}}$ .则有
$g(n+1)+\frac{\alpha }{\beta } g(n)=\frac{1}{\beta }$ ,设 $g(n+1)+\lambda =-\frac{\alpha }{\beta } (g(n)+\lambda )$ ,
解得 $\lambda =-\frac{1}{\alpha +\beta }$ ，即{ $g(n)+\lambda$ }是等比数列。这样就有
$g(n)+\lambda=(-\frac{\alpha }{\beta } )^{n-1} (\frac{1}{\beta } +\lambda )$
到了现在，把上述解出的结果全部带入上式，稍作变形，我们就可以写出斐波那契数列的通项公式了

$f(n)=\frac{1}{\sqrt{5} } [(\frac{1+\sqrt{5} }{2} )^{n}-(\frac{1-\sqrt{5} }{2} )^{n}]$

这个方法还是比较麻烦的，但是非常基础。事实上还有其他更简单的方法。

（2）线性代数解法
这个解法首先用到
$\begin{bmatrix}Fib(n+1) \\Fib(n)\end {bmatrix}=\begin{bmatrix}1&1 \\1&0\end{bmatrix}^{n}\begin{bmatrix}Fib(1) \\Fib(0)\end{bmatrix}$

公式，如果可以找到矩阵 $P$ 使得 $PAP^{-1}$ 为对角阵，我们就可以求出通项。下面需要一些高等代数知识，没学过的可直接跳过。
首先令 $|\lambda E-A|=0$ ,解得两个特征根
$\lambda_{1}=\frac{1-\sqrt{5} }{2} ,\lambda_{2}=\frac{1+\sqrt{5} }{2}$
两个特征向量为
$\alpha _{1}=[1,\frac{1+\sqrt{5} }{2} ] ^{T},\alpha _{2}=[1,\frac{-1+\sqrt{5} }{2} ] ^{T},$ 则

$P=\begin{bmatrix}1&1 \\\frac{1+\sqrt{5}}{2} & \frac{\sqrt{5}-1}{2}\end{bmatrix},P^{-1}=\begin{bmatrix}\frac{1-\sqrt{5}}{2}&1 \\\frac{1+\sqrt{5}}{2}&-1\end{bmatrix}$
而
$(PAP^{-1})^{n}=PAP^{-1}PAP^{-1}...PAP^{-1}=PA(P^{-1}P)A(P^{-1}P)A...AP^{-1}=PA^{n}P^{-1}$
解出 $A^{n}=P^{-1}(PAP^{-1})^{n}P$ ,中间矩阵的n次方可以直接求出来：

$\begin{bmatrix}\frac {1-\sqrt{5}}{2}&0 \\0&\frac {1+\sqrt{5}}{2}\end{bmatrix}^{n}=\begin{bmatrix}(\frac {1-\sqrt{5}}{2})^{n}&0\\0&(\frac {1+\sqrt{5}}{2})^n\end{bmatrix}$

然后可以轻易得到通项公式，上边已经给出，这里不再赘述。

（3）特征方程解法

通过方法（2），我们可以推导出一般的线性递推数列的通项求解方法，也就是特征方程法。我们可以发现，对于这种数列，通项总是可以表示为 $f(n)=C_{1} \lambda _{1}^{n} +C_{2} \lambda _{2}^{n}$ 的形式，因此可以直接利用已知项求解 $C_{1}$ ， $C_{2}$ 。具体做法如下：

a.由递推数列构造特征方程 $x^{2}=x+1$ ，解出两个特征值 $\lambda_{1}=\frac{1-\sqrt{5} }{2} ,\lambda_{2}=\frac{1+\sqrt{5} }{2}$ 。

b.带入 $f(0),f(1)$ ,列出如下方程：

$C_{1} +C_{1} =0$
$\frac{1-\sqrt{5} }{2} C_{1} +\frac{1+\sqrt{5} }{2} C_{2} =1$

解得 $C_{1} =-\frac{1}{\sqrt{5} } ,C_{2} =\frac{1}{\sqrt{5} } .$ 这样直接写出通项公式，是比较简单的做法。

（4）母函数法（此方法涉及组合数学知识）

设斐波那契数列的母函数为 $G(x)$ ,即
$G(x)=F_{0} +F_{1}x+F_{2}x^{2}+L+F_{n}x^{n}$
$=1+x+(F_{0}+F_{1})x^{2}+L+(F_{n-1} +F_{n-2})x^{n}$
$=1+(x+F_{1}x^{2}+F_{2}x^{3}+L+)+(F_{0}x^{2}+F_{1}x^3+L)$
$=1+(x+x^{2})G(x)$
解得 $G(x)=\frac{1}{1-x-x^{2}} =\frac{1}{\sqrt{5} } \frac{1+\sqrt{5} }{2}\frac{1}{1-\frac{1+\sqrt{5} }{2}x} -\frac{1}{\sqrt{5} } \frac{1-\sqrt{5} }{2}\frac{1}{1-\frac{1-\sqrt{5} }{2}x}$

再由幂级数展开公式 $\frac{1}{1-x}=1+x+x^{2}+$ ……

合并同类项并与 $G(x)$ 的系数比较即可。

到这里，求解斐波那契数列通项的方法就说的差不多了。无论是计算机求解还是数学推导，都体现出了非常多的技巧。而斐波那契数列的许多特性，就更加有意思了。

三、斐波那契数列的数学性质

1.与黄金比的关系

由通项公式，求相邻两项的商的极限，结果是黄金比，所以斐波那契数列又称为黄金比数列。斐波那契数列和黄金比还和一个有趣的数学概念——连分数有关：

2.一些简单的规律

（1）任意连续四个斐波那契数，可以构造出一个毕达哥拉斯三元组。如取1,1,2,3.
中间两数相乘再乘2 ==》 4
外层2数乘积==》3
中间两数平方和==》5
得到3,4,5.
下一组是5,12,13,，有兴趣的读者可以再试着推一推，证明也是容易的。

（2）整除性

每3个连续的斐波那契数有且只有一个被2整除，

每4个连续的斐波那契数有且只有一个被3整除，

每5个连续的斐波那契数有且只有一个被5整除，

每6个连续的斐波那契数有且只有一个被8整除，

每7个连续的斐波那契数有且只有一个被13整除，

…………

每n个连续的斐波那契数有且只有一个被 $f(n)$ 整除.

（3）一些恒等式

3.杨辉三角中的斐波那契数列

如图所示，每条斜线上的数的和就构成斐波那契数列。

即有 $f(n)=C_{n-1}^{0} +C_{n-2}^{1}+L+C_{n-1-m}^{m}$

4.相关数列：卢卡斯（Lucas）数列

卢卡斯数列的定义除了第0项为2之外，与斐波那契数列完全一致。即

其通项公式为：

卢卡斯数列和斐波那契数列有这些关系：

$F_{2n}=F_{n}L_{n}$
$5F_{n}=L_{n-1}+L_{n+1}$
$L_{n}^{2}=5 F_{n}^{2}+4(-1)^{n}$
$\lim_{n \rightarrow \infty }{\frac{L_{n}}{F_{n}} } =\sqrt{5}$
$L_{n}=F_{n-1}+F_{n+1}$

5.组合数学

（1）一些恒等式

（2）同余特性

$(F(m),F(n))=(m,n)$
$F(m)|F(n)\Leftrightarrow m|n$

当p为大于5的素数时，有：

$F(p-(\frac{p}{5}))\equiv 0(modp)$
$F(p)\equiv (\frac{p}{5}) (modp)$
$F(p+(\frac{p}{5}))\equiv 1(modp)$

其中

斐波那契数列还有许许多多的性质，我就不再一一介绍了。跑题了这么久，终于开始要真正回答问题了：斐波那契数列有什么用？

四、斐波那契数列的应用

1.算法

a.斐波那契堆

斐波那契堆(Fibonacci heap)是计算机科学中最小堆有序树的集合。它和二项式堆有类似的性质，可用于实现合并优先队列。特点是不涉及删除元素的操作有O(1)的平摊时间，用途包括稠密图每次Decrease－key只要O(1)的平摊时间，和二项堆的O(lgn)相比是巨大的改进。

斐波那契堆由一组最小堆构成，这些最小堆是有根的无序树。可以进行插入、查找、合并和删除等操作
1）插入：创建一个仅包含一个节点的新的斐波纳契堆，然后执行堆合并
2）查找：由于用一个指针指向了具有最小值的根节点，因此查找最小的节点是平凡的操作。
3）合并：简单合并两个斐波纳契堆的根表。即把两个斐波纳契堆的所有树的根首尾衔接并置。
4）删除（释放）最小节点
分为三步：
查找最小的根节点并删除它，其所有的子节点都加入堆的根表，即它的子树都成为堆所包含的树；
需要查找并维护堆的最小根节点，但这耗时较大。为此，同时完成堆的维护：对堆当前包含的树的度数从低到高，迭代执行具有相同度数的树的合并并实现最小树化调整，使得堆包含的树具有不同的度数。这一步使用一个数组，数组下标为根节点的度数，数组的值为指向该根节点指针。如果发现具有相同度数的其他根节点则合并两棵树并维护该数组的状态。
对当前堆的所有根节点查找最小的根节点。
5）降低一个点的键值：对一个节点的键值降低后，自键值降低的节点开始自下而上的迭代执行下述操作，直至到根节点或一个未被标记（marked）节点为止：
如果当前节点键值小于其父节点的键值，则把该节点及其子树摘下来作为堆的新树的根节点；其原父节点如果是被标记（marked）节点，则也被摘下来作为堆的新树的根节点；如果其原父节点不是被标记（marked）节点且不是根节点，则其原父节点被加标记。
如果堆的新树的根节点被标记（marked），则去除该标记。
6）删除节点：把被删除节点的键值调整为负无穷小，然后执行“降低一个节点的键值”算法，然后再执行“删除最小节点”算法。
斐波那契堆

b.欧几里得算法的时间复杂度

欧几里得算法是求解两个正整数最大公约数的算法，又称辗转相除法。代码如下：

int gcd(int a,int b){    return b ? gcd(b,a%b) : a;}

在最坏的情况下，我们可以证明，若a较小，需要计算的次数为n，则 $a>F(n-1)$ .虽然说一般分析的时候会当成对数阶，但数论最常用的欧几里得算法竟然与斐波那契数列有关，也确实是很让人吃惊呢。

2.物理学：氢原子能级问题

假定我们现在有一些氢气原子，一个电子最初所处的位置是最低的能级（Ground lever of energy），属于稳定状态。它能获得一个能量子或二个能量子（Quanta of energy）而使它上升到第一能级或者第二能级。但是在第一级的电子如失掉一个能量子就会下降到最低能级，它如获得一个能量子就会上升到第二级来。

现在研究气体吸收和放出能量的情形，假定最初电子是处在稳定状态即零能级，然后让它吸收能量，这电子可以跳到第1能级或第2能级。然后再让这气体放射能量，这时电子在1级能级的就要下降到0能级，而在第2能级的可能下降到0能级或者第1能级的位置去。

电子所处的状态可能的情形是：1、2、3、5、8、13、21…种。这是斐波那契数列的一部份。

3.自然界：植物的生长

科学家发现，一些植物的花瓣、萼片、果实的数目以及排列的方式上，都有一个神奇的规律，它们都非常符合著名的斐波那契数列。例如：蓟，它们的头部几乎呈球状。在下图中，你可以看到两条不同方向的螺旋。我们可以数一下，顺时针旋转的（和左边那条旋转方向相同）螺旋一共有13条，而逆时针旋转的则有21条。此外还有菊花、向日葵、松果、菠萝等都是按这种方式生长的。

还有菠萝、松子等，也都符合这个特点，一般会出现34,55，89和144这几个数字。

最后上一张“斐波那契树”的图片：

是的，这玩意就长这样，这种植物是存在的。

4.波浪理论与股市

这个答主不懂，大家可自行阅读文章波浪理论斐波那契数列与黄金分割率。
不过波浪的形状确实符合下边要说的斐波那契螺旋：

5.斐波那契螺旋

斐波那契螺旋又称黄金螺旋，在自然界中广泛存在。如图是一个边长为斐波那契数列的正方形组成的矩形。

（加一句：看着这个图，是不是能发现

是显而易见的？）

这样连起来就是斐波那契螺旋了

贝壳螺旋轮廓线

向日葵的生长

神奇的花

6.建筑学

7.据说一个小男孩参考斐波那契数列发明了太阳能电池树：

一名13岁的男孩根据斐波那契数列发明了太阳能电池树，其产生的电力比太阳能光伏电池阵列多20-50%。斐波那契数列类似从0和1开始，之后的数是之前两数的和，如0，1，1，2，3，5，8，13，21...Aidan Dwye在观察树枝分叉时发现它的分布模式类似斐波那契数列，这是大自然演化的一种结果，可能有助于树叶进行光合作用。
因此，Dwye猜想为什么不按照斐波那契数列排列太阳能电池？他设计了太阳能电池树，发现它的输出电力提高了20%，每天接受光照的时间延长了2.5小时。

8.斐波那契螺旋形的摇椅

妈妈摇椅是设计师Patrick Messier为自己的妻子兼合作伙伴Sophie Fournier设计的，当时他们刚有了第一个宝宝。
当Sophie宣布自己怀孕时，她说想要一把摇椅，但发现没有一把摇椅能满足美观舒适的标准，于是Patrick决定自己做一把。
于是就有了这把妈妈摇椅。像是一个飘在空中的丝带，由一片纤维玻璃做成，曲线服从斐波那契数列分布，经过特殊的高光聚氨酯处理。

五、数学上的扩展

（1）广义斐波那契数列
定义： $a+b,ab\in Z$ ,数列 $f(n)$ 满足：

其通项为：

当 $a+b=1,ab=-1$ 时即为斐波那契数列。

（2）反斐波那契数列

定义： $g(n+2)=g(n)-g(n+1)$
反斐波那契数列相邻项比值的极限为 $-0.618$ 。

（3）巴都万数列(A000931 - OEIS)
斐波那契数列可以刻画矩形，而巴都万数列则刻画的是三角形。其定义如下：

(4)未解之谜：角谷猜想

对一个正整数，若为奇数则乘3加1，若为偶数则除以2，通过有限次这样的操作，能否使得该数变成1？
这个猜想和斐波那契数列又很大关系，具体的可以看角谷猜想的斐波那契数列现象。

六、总结

斐波那契数列是各个学科中都出现的小滑头，它许多漂亮的性质让我们着迷。上文我所描述的这些只是它的冰山一角，权当抛砖引玉。大家读完了我的答案，还可以再结合自己的专业去看一些相关的资料，更好的去了解这个有趣的数列。

七、参考文献

[1]http://www.hytc.cn/xsjl/szh/lec5.pdf
[2]斐波那契数列_一米阳光
[3]斐波那契数列的规律性
[4]13岁男孩根据斐波那契数列发明太阳能电池树_cnBeta 人物_cnBeta.COM
[5]服从斐波那契数列分布的妈妈摇椅
[6]从斐波那契数列到黄金分割
[7]斐波那契《计算之书》的研究.pdf 全文文档投稿网
[8]斐波那契数列
['9]費氏數列
[10]巴都萬數列
[11]http://zh.wikipedia.org/wiki/%E5%8D%A2%E5%8D%A1%E6%96%AF%E6%95%B0
[12]角谷猜想的斐波那契数列现象
[13]The On-Line Encyclopedia of Integer Sequences® (OEIS®)
[14]波浪理论斐波那契数列与黄金分割率

阅读全文

0 0