差分约束初学整合
来源:互联网 发布:c语言全屏玫瑰花代码 编辑:程序博客网 时间:2024/06/05 14:19

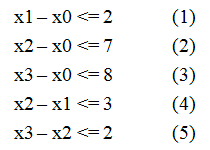


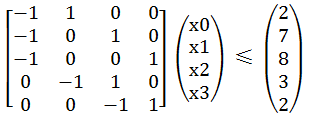
d[v] = d[u] + w(u, v);
}




2、区间约束
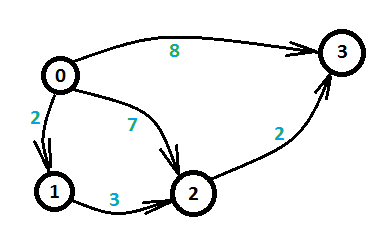
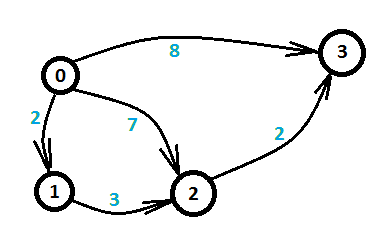
差分约束系统就是给出一些形如x-y<=b不等式的约束,问你是否有满足问题的解,或者求最小,最大解。
这个问题的神奇之处是可以转化为图论的最短路问题。
一、预备知识:SPFA算法
详见我的最短路算法详解(Dijkstra/SPFA/Floyd)
二、差分约束的转化原理
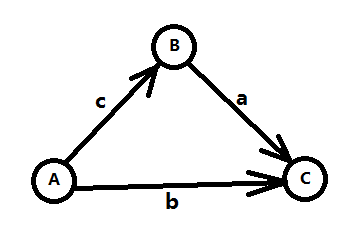
对于图论的最短路径,有:对于d(v) <= d(u) + w(u, v) ,而差分约束系统的解法利用到了单源最短路径问题中的三角形不等式。
移项得:d(v) - d(u) <= w(u, v),是不是和上面的x-y<=b的一样?
是的,这就是转化为最短路径算法的原理。
三、建图
根据题目的意思进建图。
如POJ 1201
题目大意:
有一个序列,题目用n个整数组合 [ai,bi,ci]来描述它,[ai,bi,ci]表示在该序列中处于[ai,bi]这个区间的整数至少有ci个。如果存在这样的序列,请求出满足题目要求的最短的序列长度是多少。
思路:
设s[i]为从1~i的整数个数。
这样对于区间[ a , b]显然有 S[b] - S[a-1] >=c[i] (为什么是a-1?因为闭区间a也要选上呀)
然后还有
0<= S[B]-S[B-1] <=1 (整数的话最多比前一个大一,好吧,我大二- -|||我不二啊!!)
变形得:
S[B]-S[B-1] >=0
S[B-1]-S[B]>=-1
四、用SPFA解需要注意的:
1.原图可能不是连通图,故需要加一个超级源点S,从S到任意的顶点边权为0,然后从该点出发。为什么?添加从虚点S到每个顶点的权为0的边.这是为了保证构造出来的图是连通的.由于虚点本身并不引入负圈,所以设置虚点以后最短路仍然存在,并且每个约束仍然满足.
或者差分约束不用什么附加顶点, 附加顶点的唯一用处就是保证图的连通性, 不让你有负环判不到的情况, 解决这种问题的最佳途径就是初始把所有顶点都加入队列, 并且将所有dis
置0, 这就相当于加了一个不存在的附加顶点, 它与所有的顶点的直连长度都是0.
当然推荐第二种,效率也高。
2.如果求最小的解,那么我们一开始把dis设为无穷小,并且使用最长路。即 if(d[v] < d[u]+w(u,v)) 进行更新,而建图的时候也要用大于等于。
如果求最大,那么我们一开始把dis设为无穷大,使用最短路。
为什么?
问得好!(- -|||) 以求解最大的为例(最小解同理)dis[id]一开始为无穷大,图最短路更新的条件为: if(d[v]>d[u]+w(u,v)) d[v]=d[u]+w(u,v); 通过不断的松弛,使得d的值不断变小,直到满足所有条件,也就是说满足条件的时候就是最大的了~
那么,我们建图的时,都转化为A-B<=C这种形式,以(B为起点,向A连接一条权值为C的边) 因为图的最短路有:d[v]- d[u]<=w(u,v); 即( d[v]<=d[u]+w(u,v); )
所以,当你在纠结用小于号大于号的时候,看看题目求的是最大还是最小,如果只是判断有木有解,那么大于号小于都可以,只不过要注意全部等式要统一。
题目:
ZOJ 2770 Burn theLinked Camp差分约束 ZOJ排名第一~
POJ 1201 Intervals|| POJ 1716 Integer Intervals差分约束
POJ 2983 Is theInformation Reliable?依旧差分约束
POJ 1275 CashierEmployment挺难的差分约束题
POJ 1364 King (UVA515)差分约束
POJ 3159 Candies还是差分约束(栈的SPFA)
POJ 3169 Layout差分约束
UVA 11478 - Halum差分约束
转自:http://972169909-qq-com.iteye.com/blog/1185527
先总结下:
第一:
感觉难点在于建图
第二:
①:对于差分不等式,a - b <= c ,建一条 b 到 a 的权值为 c 的边,求的是最短路,得到的是最大值
②:对于不等式 a - b >= c ,建一条 b 到 a 的权值为 c 的边,求的是最长路,得到的是最小值
③:存在负环的话是无解
④:求不出最短路(dist[ ]没有得到更新)的话是任意解
第三:
一种建图方法:
设x[i]是第i位置(或时刻)的值(跟所求值的属性一样),那么把x[i]看成数列,前n项和为s[n],则x[i] = s[i] - s[i-1];
那么这样就可以最起码建立起类似这样的一个关系:0 <= s[i] - s[i-1] <= 1;
其他关系就要去题目探索了
回到上面那些题目:
第一题:【POJ 1201/ZOJ 1508/HDU 1384 Intervals】
http://poj.org/problem?id=1201
题意:求符合题意的最小集合的元素个数
设x[i]是{i}这个集合跟所求未知集合的交集元素个数,明显最大只能是1
再设s[i] = x[0] + x[1] + …… + x[i]
明显的,s[i]表示集合{0,1,2,3,……,i}与所求未知集合的交集元素个数
那么就有x[i] = s[i] - s[i-1]
∵0 <= x[i] <= 1
∴0 <= s[i] - s[i-1] <= 1
由于题目求最小值,所以是最长路,用的是a - b >= c这种形式
即有:①s[i] - s[i-1] >= 0; ②s[i-1] - s[i] >= -1;
按照题目输入a, b, c:
表示{a,a+1,a+2,……,b}(设这个集合是Q)与所求未知集合的交集元素个数至少为c
而s[a-1]表示{1,2,3,……,a-1}与所求未知集合的交集元素个数
s[b]表示{1,2,3,……,a-1,a,a+1,a+2,……,b}与所求未知集合的交集元素个数
∴Q = s[b] - s[a-1];
即可建立关系: ③s[b] - s[a-1] >= c;
但是还有一个问题a >= 0,那么a-1有可能不合法
解决方法:所有元素+1就可以了
实现:把③变成 s[b+1] - s[a] >= c;
第二题:【POJ 1275/ZOJ 1420/HDU 1529 Cashier Employment】
http://poj.org/problem?id=1275
文章最后有附上这题的代码。
这题是这里面最难的一题,建图难,而且难以找出所有约束条件
先说明一下,这里我把编号设定为1-24,而不是题目的0-23,并且设0为虚点
设x[i]是实际雇用的i时刻开始工作的员工数
R[i]是题目需要的i时刻正在工作的最少员工数
注意了,i时刻开始工作跟i时刻正在工作是完全不同的
设s[i] = x[1] + x[2] + …… + x[i]
则s[i]表示1-i这段时间开始工作的员工数
再设num[i]表示i时刻开始工作的最多可以雇用的员工数
∴有0 <= x[i] <= num[i]
即 0 <= s[i] - s[i-1] <= num[i]
由于是求最小值,所以用最长路
则有:①s[i] - s[i-1] >= 0;②s[i-1] - s[i] >= -num[i];
(1 <= i <= 24,虽然0是虚点,但是s[1] - s[0]也是必要的!因为x[1]也是有范围的!)
由于员工可以持续工作8个小时(R[i]是i时刻正在工作的最少人数)
∴x[i-7] + x[i-6] + …… + x[i] >= R[i]【i-7开始工作的人在i时刻也在工作,其他同理】
即:③s[i] - s[i-8] >= R[i] (8 <= i <= 24)
但是有个特殊情况,就是从夜晚到凌晨的一段8小时工作时间
(x[i+17] + …… + x[24]) + (x[1] + x[2] + …… + x[i]) >= R[i];
则:s[24] - s[i+16] + s[i] >= R[i];
整理一下:④s[i] - s[i+16] >= R[i] - s[24];
(1 <= i < 8,注意i=0是没有意义的,因为R[0]没有意义)
由于s[24]就是全天实际雇用的人数,而一共有n个员工可以雇用
所以设ans = s[24]
则:⑤s[i] - s[i+16] >= R[i] - ans;( 1 <= i < 8 )
所以就可以从小到大暴力枚举ans【或二分枚举】,通过spfa检验是否有解即可【存在负环无解】
但是还有一个问题,起点在哪里……
这时候虚点0就起作用了,我称它为超级起点

于是建图后直接判断spfa(0)是否有解就可以了
PS:还有另外一个条件必须用到……:⑥s[24] - s[0] >= ans]
不用这个条件二分枚举ans可以AC,但这只是数据问题,暴力从小到大枚举木有这条件就会错,所以说这个条件最关键而又难找……要仔细找特殊点和虚点的约束关系
第三题:【POJ 1364/ZOJ 1260/HDU 1531 King】
http://poj.org/problem?id=1364
设s[i] = a[1] + a[2] + …… + a[i];
a[Si] + a[Si+1] + ... + a[Si+ni] = s[Si+ni] - s[Si-1];
所以由题意有:
①s[Si+ni] - s[Si-1] > ki
或②s[Si+ni] - s[Si-1] < ki
由于只是检验是否有解,所以最短路或最长路都可用,以下是最短路要建立的关系:
把①化为:s[si-1] - s[si+ni] <= - ki - 1
把②化为:s[si+ni] - s[si-1] <= ki - 1
第四题:【ZOJ 1455/HDU 1534 Schedule Problem】
http://acm.zju.edu.cn/onlinejudge/showProblem.do?problemCode=1455
设第i项工作持续时间为v[i],开始时间s[i],那么结束时间就是s[i]+v[i]
SAS: s[a] >= s[b] ---> s[a] - s[b] >= 0
FAS: s[a] + v[a] >= s[b] ---> s[a] - s[b] >= -v[a]
SAF: s[a] >= s[b] + v[b] ---> s[a] - s[b] >= v[b]
FAF: s[a] + v[a] >= s[b] + v[b] ---> s[a] - s[b] >= v[b] - v[a]
直接最长路建图就可以了
第五题:【HDU 3440 House Man】
http://acm.hdu.edu.cn/showproblem.php?pid=3440
此题难度仅次于第二题,需要深刻理解差分约束
题意:按照序号从左往右放置房子,求最后从低到高跳到所有房子的【最大总水平路程】
设s(b) - s(a) <= K(一个常数)表示【设a,b为序号】:
b到a的距离 <= K,但是必须定一个规则,a在左边还是b在左边?
这里设a,b是x轴上的点,再设b > a
所以这样的情况下规则就是:【s(序号大的) - s(序号小的)】才表示:【b到a之间的距离】这个意义
当然可以设另一种规则---【序号小-序号大】表示距离---,总之要一致!
按照第一种规则有以下关系:
①位置相邻:
s(i) - s(i-1) >= 1 ---> s(i-1) - s(i) <= -1
②高度相邻(排序后):【num表示a[i]这间房子的序号】
s(max(a[i].num,a[i-1].num))-s(min(a[i].num,a[i-1].num)) <= D
建图后只要这样:
spfa (min (a[1].num, a[n].num));
printf ("%d\n", dist[max (a[n].num, a[1].num)]);
答案就出来了
另外推荐这种方法!比较简单:http://hi.baidu.com/tju_ant/blog/item/f22fe6d92809033833fa1c08.html
第六题:【HDU 3592 World Exhibition】
http://acm.hdu.edu.cn/showproblem.php?pid=3592
按照题目明显条件建立关系式立刻水过
但是我觉得它数据很水……
题目说:Assume that there are N (2 <= N <= 1,000) people numbered 1..N who are standing in the same order as they are numbered
也就是说人是按序号排的啊
那应该还有一个约束条件才对吧:s(i) - s(i-1) >= 0;
就像这组数据:
1
3 2 1
1 2 1
1 3 2
2 3 3
要按序号排队不可能满足,应该输出-1
总之要不要这个约束条件都能AC……我特么的彻底无语了

第七题:【HDU 3666 THE MATRIX PROBLEM】
http://acm.hdu.edu.cn/showproblem.php?pid=3666
这题spfa用队列卡数据容易超时,用栈吧……
由题意得对于矩阵每个元素【设为w,处于矩阵第i行,第j列】
L <= w*a[i]/b[j] <= U
两边取对数有:
lg(L) <= lg(w)+lg(a[i])-lg(b[j]) <= lg(U)
按照最长路整理得【也可以用最短路】:
①lg(a[i])-lg(b[j]) >= lg(L)-lg(w);②lg(b[j])-lg(a[i]) >= lg(w)-lg(U)
把a和b数组合并成一个数组s得【a有n个元素,b有m个元素,这里把b接在a数组后面】:
①s(i) - s(j+n) >= lg(L) - lg(w)
②s(j+n) - s(i) >= lg(w) - lg(U)
最后加个超级起点即可
我把0作为超级起点:
for (i = 1; i <= n + m; i++)
addedge (0, i, 0);
spfa (0);
最后弱弱的献上第二题代码:
- #include <iostream>
- #include <queue>
- using namespace std;
- #define inf 0x7fffffff
- #define M 25
- struct edge{
- int v, w, next;
- }e[5*M];
- bool inq[M];
- int dist[M], pre[M], n = 24, cnt, ind[M];
- void init ()
- {
- memset (pre, -1, sizeof(pre)); cnt = 0;
- }
- void addedge (int u, int v, int w)
- {
- e[cnt].v = v; e[cnt].w = w; e[cnt].next = pre[u]; pre[u] = cnt++;
- }
- bool spfa (int u)
- {
- int i, v, w;
- for (i = 0; i <= n; i++)
- {
- dist[i] = -inf;
- inq[i] = false;
- ind[i] = 0;
- }
- queue<int> q;
- q.push (u);
- inq[u] = true;
- dist[u] = 0;
- while (!q.empty())
- {
- u = q.front();
- if (++ind[u] > n)
- return false;
- q.pop();
- inq[u] = false;
- for (i = pre[u]; i != -1; i = e[i].next)
- {
- v = e[i].v;
- w = e[i].w;
- if (dist[u] + w > dist[v])
- {
- dist[v] = dist[u] + w;
- if (!inq[v])
- {
- q.push (v);
- inq[v] = true;
- }
- }
- }
- }
- return true;
- }
- int main()
- {
- int t, R[M], num[M], i, pos, m, l, r, ans;
- scanf ("%d", &t);
- while (t--)
- {
- for (i = 1; i <= n; i++)
- scanf ("%d", R+i);
- scanf ("%d", &m);
- memset (num, 0, sizeof(num));
- for (i = 0; i < m; i++)
- {
- scanf ("%d", &pos);
- num[pos+1]++;
- }
- l = 0, r = m;
- bool flag = true;
- while (l < r) //二分枚举ans
- {
- init();
- ans = (l+r) / 2;
- for (i = 1; i <= n; i++)
- {
- addedge (i-1, i, 0); //s[i] - s[i-1] >= 0
- addedge (i, i-1, -num[i]); //s[i-1] - s[i] >= -num[i]
- }
- for (i = 8; i <= n; i++)
- addedge (i-8, i, R[i]); //s[i] - s[i-8] >= R[i]
- for (i = 1; i < 8; i++)
- addedge (i+16, i, R[i]-ans); //s[i] - s[i+16] >= R[i] - ans
- addedge (0, 24, ans); //s[24] - s[0] >= ans
- if (spfa (0))
- r = ans, flag = false;
- else l = ans + 1;
- }
- if (flag)
- puts ("No Solution");
- else printf ("%d\n", r);
- }
- return 0;
- }
差分约束系统只是对最短路算法的一种应用,没有什么新的算法,只是对于具体问题的建图方法的确定
----------------------------------------------差分约束系统解决的问题描述---------------------------------------------------------
差分约束系统解决的问题是不等式组的求解:
X1 - X2 <= 0
X1 - X5 <= -1
X2 - X5 <= 1
X3 - X1 <= 5
X4 - X1 <= 4
X4 - X3 <= -1
X5 - X3 <= -3
X5 - X4 <= -3
这就是一个不等式组,给出的不等式组只存在小于等于号,如果有个别的式子是大于等于,我们可以通过两边同时乘-1的得到统一的不等号方向的不等式组。
这个不等式组一定是无解和无数解两种情况,因为如果是存在任意一组解,{x1,x2,x3,x4,x5},我们都可以通过{x1+k,x2+k,x3+k,x4+k,x5+k}得到一个新的解。所以解的个数是无数的。
因为每个数都加k,他们任意两个数之间的差是不变的,所以对于不等式没有影响。
------------------------------------解决差分约束问题的建图方法-及解决方案-------------------------------------------------------
1.对于一个全部都是<=号的不等式组,我们可以将每个式子转化为Xi<=Xj+W(i,j),那么就建一条边,Xj->Xi=W(i,j),然后利用最短路径解决问题,在x0定死的情况下,求得最小值
2.对于一个全部都是>=号的不等式组,我们可以将每个式子转化为Xi>=Xj+W(i,j),那么就建一条边,Xj->Xi=W(i,j),然后利用最长路径解决问题,在x0定死的情况下,求得最大值
如果dis[Xi]为inf或-inf,那么Xi为任意解
如果求最短路的过程中出现负环,那么说明该不等式组无解
--------------------------------------建图方法和解决方案的证明-------------------------------------------------------------------------
1.我们在这里规定dis[x]就是xi的值,那么在最短路的结果中中我们保证的是如果存在两点相连,dis[i]-dis[j] <= w(i,j),正好和不等式组中的式子相符,x0定死,相当于给原点dis[S]==C一个固定的常数值,那么相当于dis[i]求取的都是最小的,那么相当于得到了最小解
2.>=号和最长路的对应关系类似
3.当dis[Xi]==inf 或者 -inf时,那么证明,当前点和原点之间不存在一条路径,那么不能够得到一组确定的解,没有最优解
4.当出现负环的时候,证明无解,因为存在负环的时候,
Xi <= Xj + a
Xj <= Xi + b
若a+b<0的时候存在负环,
这时
两式相加,Xi+Xj <= Xi+Xj+a+b,若a+b<0
那么0<= a+b ,矛盾!!
所以方程无解
- 差分约束初学整合
- 【图-差分约束】 差分约束
- 差分约束系统
- 差分约束系统
- 差分约束系统
- 差分约束系统
- POJ_1364_差分约束
- 差分约束系统
- 差分约束
- 差分约束 模板
- 差分约束系统
- 差分约束系统
- 差分约束系统
- Poj1275 差分约束
- 【差分约束系统】
- poj1364 差分约束
- hdu1534差分约束
- 差分约束
- 文章标题
- Python String 的replace()与List的remove()
- css定位
- Java约瑟夫问题(丢手帕)的双向循环实现
- Ajax中window.location.href无法跳转的解决办法
- 差分约束初学整合
- 计蒜客 2017 复赛 腾讯消消乐 (状压dp)
- git学习(4)_远程与github
- TensorFlow 图像处理和解码操作函数概述
- 安装Delphi2007的时候出现未找到变量HAS_SLIP的定义
- Java I/O模型从BIO到NIO和Reactor模式
- js函数内部调用的含有回掉的函数,其中回掉函数可以拿到外部函数传递的实参
- 学习java第一天
- java时间差计算


