HDU 6073 Matching In Multiplication

Matching In Multiplication

Problem Description

In the mathematical discipline of graph theory, a bipartite graph is a graph whose vertices can be divided into two disjoint sets U and V (that is, U and V are each independent sets) such that every edge connects a vertex in U to one in V. Vertex sets U and V are usually called the parts of the graph. Equivalently, a bipartite graph is a graph that does not contain any odd-length cycles. A matching in a graph is a set of edges without common vertices. A perfect matching is a matching that each vertice is covered by an edge in the set.



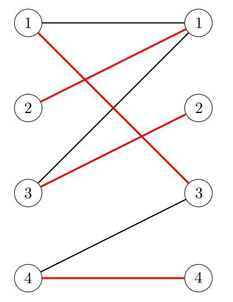
Little Q misunderstands the definition of bipartite graph, he thinks the size of U is equal to the size of V, and for each vertex p in U, there are exactly two edges from p. Based on such weighted graph, he defines the weight of a perfect matching as the product of all the edges' weight, and the weight of a graph is the sum of all the perfect matchings' weight.

Please write a program to compute the weight of a weighted ''bipartite graph'' made by Little Q.

 

Input

The first line of the input contains an integer T(1≤T≤15), denoting the number of test cases.

In each test case, there is an integer n(1≤n≤300000) in the first line, denoting the size of U. The vertex in U and V are labeled by 1,2,...,n.

For the next n lines, each line contains 4 integers vi,1,wi,1,vi,2,wi,2(1≤vi,j≤n,1≤wi,j≤109), denoting there is an edge between Ui and Vvi,1, weighted wi,1, and there is another edge between Ui and Vvi,2, weighted wi,2.

It is guaranteed that each graph has at least one perfect matchings, and there are at most one edge between every pair of vertex.

 

Output

For each test case, print a single line containing an integer, denoting the weight of the given graph. Since the answer may be very large, please print the answer modulo 998244353.

 

Sample Input

122 1 1 41 4 2 3

 

Sample Output

16

 

Source

2017 Multi-University Training Contest - Team 4

题意：T组测试数据，给出两个顶点集合，左边为U，右边为V，每个顶点集合的大小为n，然后有n行输入，第i行的输入v1，w1，v2，w2，表示集合U中的i顶点与集合V中的v1，v2顶点相连，且边的权值为w1，w2。求两个集合的所有完美匹配的权值之和。一个完美匹配的权值为该匹配所有边的权值相乘，且数据保证至少存在一个完美匹配。

分析：题目保证至少存在一个完美匹配，U中所有顶点的度数都等于2，V中所有顶点的度数都大于等于1，那么对于V中度数为1的点，它们对所有完美匹配的权值的贡献common是不变的，因此，我们可以先处理V中度数为1的点。假设V中度数为1的点有k个，那么在U中我就需要用k个点来与V中的k个度数为1的点匹配，然后U和V中都剩下m个点，m=(n-k)。此时我们可以知道U和V中所有点的度数都大于等于2了。（U中会存在度数为1的点吗？不存在的。U中顶点的度数只有我们在处理V中顶点的时候才会改变，那么当我们在处理V中度数为1的顶点N的时候，说明U中只有一个顶点M跟N相连，此时的处理只涉及N和M，所以U中别的顶点的度数还是跟初始一样。）继续，U中m个顶点的度数都是2，那么V中m个顶点的总度数就是2*m，又因为此时V中m个顶点的度数都大于等于2，那么我们可以知道V中m个顶点的度数都是2。此时我们可以发现，U∪V中的所有顶点的度数都是偶数，当完美匹配完成后，此时图中必然存在欧拉回路，也就是环。对于一个环中，如O0->O1->O2->O3->O0，我们可以理解为(1)O0与O1匹配，O2和O3匹配，(2)O1和O2匹配，O3和O0匹配，也就是说，对于一个已经完成的匹配，它只存在两种方案。那么我们就可以在一个环中，通过枚举起点O0和O1来找出当前环的两种匹配权值X1，Y1。由于图中可能存在多个环，我们需要枚举U中m个点来找出所有的环，一个环对于结果的贡献值是common*(X1+Y1)；那么P个环就是common*(X1+Y1)*(X2+Y2)*....*(XP+YP)=ans

ans就是最后的结果了。

这里涉及的算法就是一个拓扑排序和求环（我还想用Tarjan来求T_T。其实只要根据已知边找出结点就行了。鶸/(ㄒoㄒ)/~~）。

下边看一下官方题解吧~

首先如果一个点的度数为$1$，那么它的匹配方案是固定的，继而我们可以去掉这一对点。通过拓扑我们可以不断去掉所有度数为$1$的点。

那么剩下的图中左右各有$m$个点，每个点度数都不小于$2$，且左边每个点度数都是$2$，而右侧总度数是$2m$，因此右侧只能是每个点度数都是$2$。这说明这个图每个连通块是个环，在环上间隔着取即可，一共两种方案。

时间复杂度$O(n)$。

#include<bits/stdc++.h>using namespace std;struct Edge{    int v;    long long w;};int n;int a,c;long long b,d;vector<Edge> vec[600005];int indegree[600005];long long common;const int mod=998244353;int vis[600005];int node[600005];int cnt;void add(int u,int v,long long w){    indegree[v]++;    Edge temp;    temp.v=v;    temp.w=w;    vec[u].push_back(temp);}void input(){    scanf("%d",&n);    for(int i=1;i<=2*n;i++){        vec[i].clear();        indegree[i]=0;        common=1;        vis[i]=0;        cnt=0;    }    for(int i=1;i<=n;i++){        scanf("%d%lld%d%lld",&a,&b,&c,&d);        add(i,a+n,b);        add(i,c+n,d);        add(a+n,i,b);        add(c+n,i,d);    }}void topo(){    queue<int> q;    for(int i=1;i<=2*n;i++){        if(indegree[i]==1){            q.push(i);        }    }    while(q.empty()==0){        int u=q.front();        q.pop();        vis[u]=1;        int len=vec[u].size();        for(int i=0;i<len;i++){            int v=vec[u][i].v;            if(vis[v]==0){                long long w=vec[u][i].w;                common*=w;                common%=mod;                vis[v]=1;                for(int j=0;j<vec[v].size();j++){                    int k=vec[v][j].v;                    indegree[k]--;                    if(vis[k]==0&&indegree[k]==1){                        q.push(k);                    }                }                break;            }        }    }    for(int i=1;i<=2*n;i++){        if(vis[i]==0){            node[++cnt]=i;        }    }}int que[600005];int find1(int cur){    int len=vec[cur].size();    for(int i=0;i<len;i++){        int v=vec[cur][i].v;        if(vis[v]==0){            return v;        }    }    return 0;}long long get(int u,int v){    int len=vec[u].size();    for(int i=0;i<len;i++){        if(vec[u][i].v==v){            return vec[u][i].w;        }    }    return 0;}void solve(){    long long ans=1;    //cout<<"ans="<<ans<<endl;    for(int i=1;i<=cnt;i++){        int u=node[i];        if(vis[u]==0){            int top=0;            vis[u]=1;            que[++top]=u;            for(int j=find1(u);j;j=find1(j)){                que[++top]=j;                vis[j]=1;            }            que[top+1]=que[1];            long long x=1;            long long y=1;            for(int j=1;j<=top;j+=2){                x=x*get(que[j],que[j+1])%mod;            }            for(int j=2;j<=top;j+=2){                y=y*get(que[j],que[j+1])%mod;            }            //printf("x=%lld y=%lld\n",x,y);            ans=ans*(x+y)%mod;        }    }    printf("%lld\n",ans*common%mod);}int main(){    int N;    //freopen("1007.in","r",stdin);    scanf("%d",&N);    while(N--){        input();        topo();        solve();    }    return 0;}