PCA与SVD学习之路

前言

由于实验室课题中用到了PCA降维，而我之前对于pca的理解一直是不够深入。不能理解得分转换矩阵系数的大小和正负的意义。特征值的内在意义。所以现在仔细研究一下，以求对其有进一步的理解。
PCA（Principal Component Analysis）通过线性变化将原始数据变换为各维度线性无关的表示，可用于提取数据的主要特征向量，常用于数据的降维[1]。

向量表示和投影

我们知道，二维空间中的一点可以用二维向量表示，如果是高维空间中的一点，则用多维向量来表示。任意两个向量的相乘可以表示为：

A⋅B=|A||B|cos(α)
A与B的内积等于A到B的投影长度乘以B的模。再进一步，如果我们假设B的模为1，即让|B|=1，那么就变成了：
A⋅B=|A|cos(α)
设向量B的模为1，则A与B的内积值等于A向B所在直线投影的矢量长度！（这是我们得到的第一个重要结论）

基

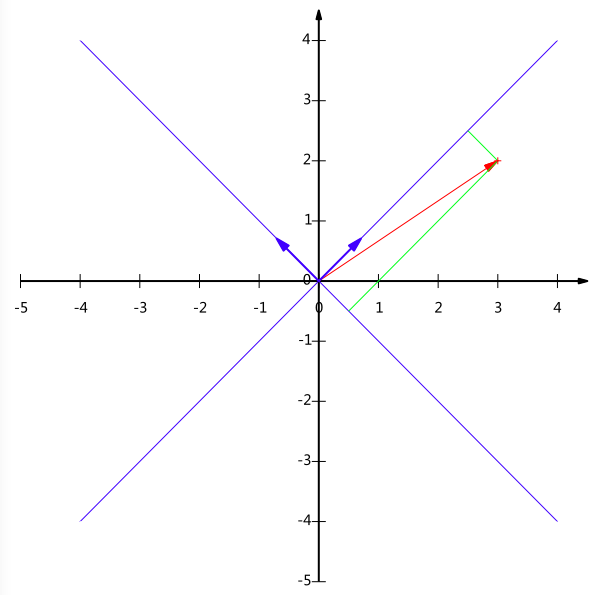
要准确描述向量，首先要确定一组基，然后给出在基所在的各个直线上的投影值就可以了。而在我们平常所用的直角坐标系中，省略了这一步，默认为以（1，0）和（0，1）为基。例如（1，1）和（1，-1）也可以成为一组基，一般来说，我们希望基的模为1，这样，任一向量与基的内积，就相当于在向量在这个方向上的投影值。所以上面的基，模为1，转换为（12√,12√）和（−12√,12√）
如果我们想获得（3，2）在新基上的坐标，即在两个方向上的投影矢量值，那么根据内积的几何意义，我们只要分别计算(3,2)和两个基的内积，不难得到新的坐标为（52√,−12√）[1]

(32)⎛⎝⎜⎜⎜12√12√−12√12√⎞⎠⎟⎟⎟=(52√−12√)

如果M个N维向量转换为新的R维空间中，首先将R个基按列组成矩阵A，然后将向量按列组成矩阵B,那么两矩阵的乘积AB就是变换结果
（未完待续…….）

方差

如果我们有一组N维向量，现在要将其降到K维（K小于N），那么我们应该如何选择K个基才能最大程度保留原有的信息？一种直观的看法是：希望投影后的投影值尽可能的分散。那如何度量这种分散程度？答案是方差来描述。
对于二维坐标系转到一维坐标系：

Var(a)=1m∑mi=1(ai−μ)2
如果我们将每一个向量已经均值化（针对每一维度的特征）了，则Var(a)=1m∑mi=1a2i
于是上面的问题被形式化表述为：寻找一个一维基，使得所有数据变换为这个基上的坐标表示后，方差值最大。

协方差

对于二维转换成一维，找到那个使得方差最大的方向就可以了，但是对于更高维度的向量来说，有一个问题需要解决，首先，在选择完第一个方向只有，如何选择第二个方向，如果只是单纯的选择方差最大的方向，那么这个第二个选择的方向应该是与第一个方向几乎重合到一块。但实际效果并没有用，因为和选择的第一个方向存在线性相关，信息重复。
首先研究一下相关性：
因为已经均值化了，所以：

Cov(a,b)=1m∑mi=1aibi
当协方差为0时，表示两个字段完全独立，为了让协方差为0，我们选择第二个基时，只能选择与第一个基正交的方向。但是如果是存在多个正交的方向呢？

我们得到了降维问题的优化目标：将一组N维向量降为K维（K大于0，小于N），其目标是选择K个单位（模为1）正交基，使得原始数据变换到这组基上后，各字段两两间协方差为0，而字段的方差则尽可能大（在正交的约束下，取最大的K个方差）。

协方差矩阵

假设我们只有两个特征维度，将其写成矩阵的形式

X=⎛⎝⎜⎜⎜⎜⎜⎜a1a2..amb1b2..bm⎞⎠⎟⎟⎟⎟⎟⎟

然后我们用X乘以X的转置，并乘上系数1/m：

1mXTX=⎛⎝⎜⎜⎜⎜⎜1m∑i=1ma2i1m∑i=1maibi1m∑i=1maibi1m∑i=1mb2i⎞⎠⎟⎟⎟⎟⎟

观察上面的公式，你会发现，方差和协方差被统一到一个矩阵中去了

协方差矩阵对角化

根据协防差矩阵以及我们之前的理解，从数学角度上来说，我们的工作就是将协方差矩阵对角化，即除对角线外的其它元素化为0，并且在对角线上将元素按大小从上到下排列。对角矩阵的所表示的意义是：对于任意两个维度的矩阵不相关，为什么要不相关？回顾一下，只能各维度不相关，才能使降维之后各个维度的方差，即信息的累加达到最大。如果相关那就存在信息的重复。

设原始数据矩阵X对应的协方差矩阵为C，而P是一组基按行组成的矩阵，设Y=PX，则Y为X对P做基变换后的数据。设Y的协方差矩阵为D，我们推导一下D与C的关系：

D=====1mYYT1m(PX)(PX)T1mPXXTPTP(1mXXT)PTPCPT

到这里我们需要注意，一开始X将每一行表示为一条记录或者说是样本，将每一列表示一个向量，也就是说，是Y=XTP的形式。而在这里设Y=PX,当然只是形式不一样,其内在一致。
到现在我们终于看到了事情的本质，我们要找的P是能让原始协方差矩阵P对角化的P。换句话说，优化目标变成了一个寻找矩阵P，满足PCPT是一个对角阵，并且对角元素按从大到小排列，那么P的前k行就是要寻找的基，用P的前K行组成的矩阵乘以X，就使得X从N维降到了K
维。

由上文知道，协方差矩阵C是一个是对称矩阵，在线性代数上，实对称矩阵有一系列非常好的性质：

1）实对称矩阵不同特征值对应的特征向量必然正交。

2）设特征向量λ重数为r，则必然存在r个线性无关的特征向量对应于λ，因此可以将这r个特征向量单位正交化。

由上面两条可知，一个n行n列的实对称矩阵一定可以找到n个单位正交特征向量，设这n个特征向量为e1,e2,⋯,en，我们将其按列组成矩阵(任意两个特征向量正交,，此时列表示某一维，下面需要转换)：

E=(e1e2⋯en)
则对协方差矩阵C有如下结论：

ETCE=Λ=⎛⎝⎜⎜⎜⎜⎜λ1λ2⋱λn⎞⎠⎟⎟⎟⎟⎟

到这里，我们发现我们已经找到了需要的矩阵P：

P=ET
P是协方差矩阵的特征向量单位化后按行排列出的矩阵，其中每一行都是C的一个特征向量。如果设P按照ΛΛ中特征值的从大到小，将特征向量从上到下排列，则用P的前K行组成的矩阵乘以原始数据矩阵X，就得到了我们需要的降维后的数据矩阵Y。

引用

[1] http://blog.codinglabs.org/articles/pca-tutorial.html