主成分分析详解（包含最大方差理论、协方差、几何意义） Principal components analysis

主成分分析

Principal components analysis

转载请注明：云南省高校数据化运营管理工程研究中心博客http://blog.csdn.net/m0_37788308/article/details/78115209

主成分分析（Principal components analysis，以下简称PCA）是最重要的降维方法之一，接下来我们分四部分来展开PCA的理论与实践：

•数据特点

• 什么是主成份分析

• 主成份分析被发明的心路历程

•python如何快速实现PCA

一、数据特点

1.维度灾难

2.变量关系不一般。

具体来说，数据分析处理时涉及的样本有很多变量，会带来分析问题的复杂性。同时，这些变量彼此之间常常存在一定程度的、有时甚至是相当高的相关性，这说明数据是有冗余的，或者说是含在观测数据中的信息是有重叠的。
（这是我们利用主成分降维的前提条件，也可以说这这使得变量降维成为可能。）
那这时我们会不会想到找到一些精华的变量，或者找到精华的综合变量呢？
（这是我们利用主成分降维的动机）

可参考被博文广传的例子：

•比如拿到一个汽车的样本，里面既有以“千米/每小时”度量的最大速度特征，也有“英里/小时”的最大速度特征，显然这两个特征有一个多余。

• 拿到一个数学系的本科生期末考试成绩单，里面有三列，一列是对数学的兴趣程度，一列是复习时间，还有一列是考试成绩。我们知道要学好数学，需要有浓厚的兴趣，所以第二项与第一项强相关，第三项和第二项也是强相关。那是不是可以合并第一项和第二项呢？

二、什么是主成分分析

1.由来：

主成分分析（principal component analysis）由皮尔逊（Pearson，1901）首先引入，后来被霍特林（Hotelling，1933）发展了。

2. 描述；

主成分分析是一种通过降维技术把多个变量化为少数几个主成分（综合变量）的统计分析方法。这些主成分能够反映原始变量的绝大部分信息，它们通常表示为原始变量的某种线性组合。
那为了主成分的为了是这些主成分所含的信息不互相重叠，应要求他们之间互不相关。
主成分的目的：
（1）变量的降维
（2）主成分的解释
（在主成分有意义的情况下主成分）

3.计算步骤

例子：（我们简单粗暴直接上例子，看例子我们带着问题，一步一步来）

在制定服装标准的过程中，对128名成年男子的身材进行了测量，每人测得的指标中含有这样六项：身高（x1）、坐高（x2） 、胸围（x3） 、手臂长（x4） 、肋围（x5）和腰围（x6） 。

第一步，对原始数据标准化（减去对应变量的均值，再除以其方差），随后计算相关矩阵

                              表1  男子身材六项指标的样本相关矩阵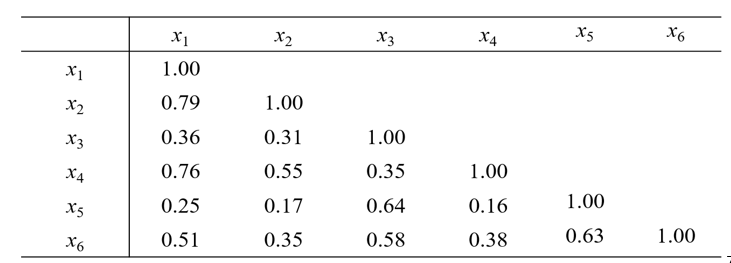

第二步，计算相关矩阵的特征值及特征向量

                              表2  的前三个特征值、特征向量以及贡献率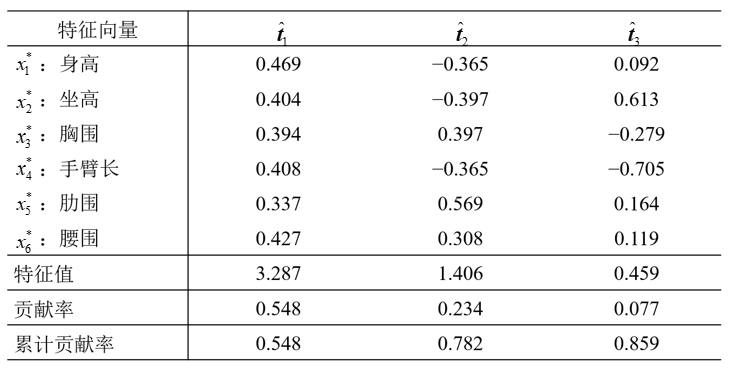

特征值从大到小排列，特征向量和特征值对应从大到小排列。

前三个主成分分别为:（输入公式）

y^1y^2y^3=0.469x∗1+0.404x∗2+0.394x∗3+0.408x∗4+0.337x∗5+0.427x∗6=−0.365x∗1−0.397x∗2+0.397x∗3−0.365x∗4+0.569x∗5+0.308x∗6=−0.092x∗1+0.613x∗2−0.279x∗3−0.705x∗4+0.164x∗5+0.119x∗6

第三步，根据累计贡献率(一般要求累积贡献率达到85%)可考虑取前面两个或三个主成分。

第四步，解释主成分。观察系数发现第一主成分系数多为正数，且变量都与身材大小有关系，称第一主成分为（身材）大小成分；类似分析，称第二主成分为形状成分（或胖瘦成分），称第三主成分为臂长成分。

（结合一定的经验和猜想，解释主成分，不是所有的主成分都能被合理的解释）

称第一主成分为（身材）大小成分，称第二主成分为形状成分（或胖瘦成分），称第三主成分为臂长成分。

可考虑取前两个主成分。

由于lambda 6(第六个特征值) 非常小，所以存在共线性关系：

λ6^t6^=0.126=(−0.786,0.433,−0.125,0.371,0.034,0.179)=−0.786x∗1+0.433x∗2−0.125x∗3+0.371x∗4+0.034x∗5+0.179x∗6≈0

第五步，计算主成分得分。即对每一个样本数据（标准化后）带入第三步的主成分公式中，计算第一主成分得分，第二主成分得分。

第六步，将主成分可画图聚类，将主成分得分看成新的因变量可线性回归。

总结一下PCA的算法步骤：

设有m条n维数据，m个样本，对原始数据标准化（减去对应变量的均值，再除以其方差），每个样本对应p个变量,x=(x∗1,x∗2,⋯，x∗n)′。

1.求出自变量的协方差矩阵（或相关系数矩阵）；（协方差矩阵参考博文： …………）

2.求出协方差矩阵（或性关系数矩阵）的特征值及对应的特征向量；

3.将特征向量按对应特征值大小从上到下按行排列成矩阵，取前k行组成矩阵a（为k*p)；(特征值特征向量参考博文…………)

4.Y（为k*1）=aT∗X 即为降维到k维后的数据;

5.可前两个主成分的散点图及聚类，也可将主成分得分作为新的变量进行回归。

4.主成分的应用

在一些应用中，这些主成分本身就是分析的目的，此时我们需要给（用来降维的前几个）主成分一个符合实际背景和意义的解释，以明白其大致的含义。

在主成分分析中，我们首先应保证所提取的前几个主成分的累计贡献率达到一个较高的水平，其次对这些被提取的主成分都能够给出符合实际背景和意义的解释。

主成分的解释其含义一般多少带有点模糊性，不像原始变量的含义那么清楚、确切，这是变量降维过程中不得不付出的代价。因此，提取的主成分个数m通常应明显小于原始变量个数p（除非p本身较小），否则维数降低的“利”可能抵不过主成分含义不如原始变量清楚的“弊”。

在更多的另一些应用中，主成分只是要达到目的的一个中间结果（或步骤），而非目的本身。例如，将主成分用于聚类（主成分聚类）、回归（主成分回归）、评估正态性、寻找异常值，以及通过方差接近于零的主成分发现原始变量间的多重共线性关系等，此时的主成分可不必给出解释。

三、主成份为什么可以？

经过主成分在压缩数据之后的数据（主成分得分数据），多个变量变为更少的综合变量，变量个数减少了，还能反映原有数据的信息吗？为什么可以呢？解决以上疑问前我们需要了解PCA理论基础：

1.PCA理论基础:方差最大理论

我们以一个二维数据为例：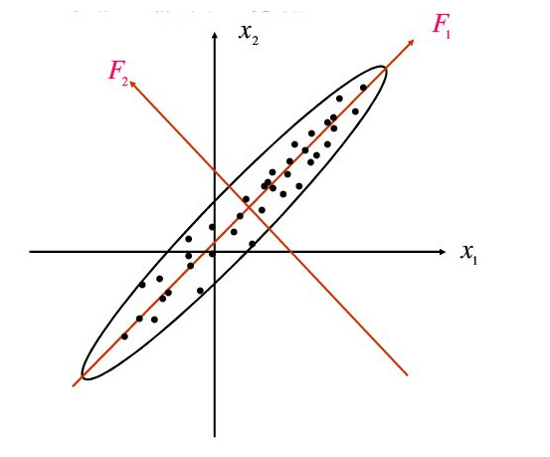

图1：寻找主成分的正交旋转
将二维，降至一维
• a二维经过投影，变为一维；
• b要尽可能保留原始信息。直观的感受就是投影之后尽量分散，点分布差异相对较大，没有相关性（相反的极端情况是投影后聚成一团，变量间的差别小，蕴含的信息就少了）；
• c如何体现差异呢，可量化的方差。这就需要找一个方向使得投影后它们在投影方向上的方差尽可能达到最大，即在此方向上所含的有关原始信息样品间的差异信息是最多的；
• d降维在线性空间中就是基变换，换一种说法就是，找到一组的基向量，在此向量空间上进行投影。在图中就是本来基是（0，1），（1,0）现在换成在横贯1,3第一象限的那条，为什么不选横贯2，4象限的呢，思考b条。

我们由二维空间向一维空间的转换，如何才能尽可能的保留信息呢，这就需要找一个方向使得投影后它们在投影方向上的方差尽可能达到最大，即在此方向上所含的有关原始信息样品间的差异信息是最多的。

（小伙伴会不会有为什么是方差最大的疑惑呢？从数据体现信息的多少出发。极端的情况是样本数据都是相同的，那就没有更多信息了。所以有样本间有变化，才有更多信息，变化就是差异，差异就用方差体现）

2.方差最大和协方差的关系

要解释方差最大和主成分的关系需要从方差和协方差的关系入手：

设对原始数据标准化（减去对应变量的均值，再除以其方差），每个样本对应p个变量，设x=(x∗1,x∗2,⋯，x∗p)′为p维随机变量,u=E(x),∑=V(x)，找其线性组合（找综合变量），进行线性变换：

⎧⎩⎨⎪⎪⎪⎪⎪⎪⎪⎪y1=y2=yp=a11x1+a21x2+⋯+a1pxpa12x1+a22x2+⋯+a2pxp⋮a1px1+a2px2+⋯+appxp=a′1x=a′2x⋮=a′px

我们首先试图用综合变量y1来代表原始的P个变量,为使y1,在 x∗1,x∗2,⋯，x∗n的一切线性组合中最大限度的保留这组变量的信息，应是其方差最大化。在a′1a1=1的约束下，寻找a1，使得
V(y1)=a′1∑a1,
达到最大,就称为第一主成分。对称矩阵协方差矩阵 。

∑=V(x)

为对称的，进行对称矩阵的谱分解，（分解后的对角矩阵元素
λi，ti
都有着特殊的含义，即特征值和对应的特征向量）
谱分解：

∑=TΛTT=(t1,t2,⋯,tp)⎛⎝⎜⎜λ10⋯⋱⋯0λp ⎞⎠⎟⎟ ⎛⎝⎜⎜⎜⎜⎜⎜⎜⎜t′1t′2⋮t′p⎞⎠⎟⎟⎟⎟⎟⎟⎟⎟=∑i=1pλit1t′1

3. 解释方差最大和主成分的关系：

设

λ1>λ2>λp≥0

由于

V(y1)=a′1∑a1=∑i=1pλia′1tit′ia1=∑i=1pλi(a′1ti)2

≤λ1∑i=1p(a′1ti)2=λ1∑i=1pa′1tit′ia1

=λ1a′1TTTa1=λ1a′1a1=λ1

(计算要知道，T为正交矩阵。t为特征向量，T’T为1；a’t是一个数，不是向量；a’a已经设定为1，本人第一次看好多遍无果，想到前面一句后才顺利的推导上面的式子)
直接验证，当取a1=t1时,有t′1∑t1=t′1(λ1t1)=λ1,即此时y1=t′1x,具有最大方差值λ1。
如果第一主成分信息不够多，还不足以代表原始的p个变量，则需要再考虑第二主成y2，为了使与y2所含的信息与y1不重叠，要求cov(y1,y2)=0.
第二主成分的推理于第一主成分类似，可得到y1=t′2x，具有方差值λ2。
（推理点拨：考虑到不同特征值的特征向量正交，相乘为0，推理亦是会畅通。）
（重叠是指线性关系上的，如果有重叠则说明还有进一步降维的空间）

贡献率和累计贡献率概念：

从上面的推导，我们也可以发现特征值和主成分方差的关系，总方差中属于第i主成分yi的比例为

λi∑i=1pλi

称为主成分yi的贡献率。累计贡献率就是多个主成分贡献率的加和啦。

主成分取多少个呢？

可人为指定固定个数，但是往往取（相对于p）较小的m个,使得累计贡献达到一个较高的百分比（80%——90%），此时y1,y2,y2……，ym可以来代替x1,x2,x3……xp,从而达到降为的目的。而信息的损失却不多。

几何意义

通过第三部分的计算过程，假设我们得到所有的主成分：
y1,y2,y3,⋯，yp,ai为特征向量.在 2.方差最大和协方差的关系部分内容中的线性变换，是一个正交变换
几何意义是将原有RP空间的由(x∗1,x∗2,⋯，x∗p)′够成的原p维坐标轴作一正交旋转，一组正交单位向量(t1,t2,⋯,tp)表明了p个新坐标轴的方向，这些新的坐标轴彼此扔保持正交，yi是在ti上的投影值，λi反映了在t1上投影点的分散程度。

四、如何实现

内部服务器博客，或者CSDN 云南省高校数据化运营管理工程研究中心的博客.

1.我们可以按步编程（见程序《PCA算法 python实现（法一）一步一步实现》）
http://blog.csdn.net/m0_37788308/article/details/78115229

2.快速代码实现（《PCA python实现（法2）scikit-learn 快速实现》）
http://blog.csdn.net/m0_37788308/article/details/78115229

sklearn官方文档地址：http://scikit-learn.org/stable/modules/generated/sklearn.decomposition.PCA.html