通俗理解卷积

来源：互联网发布：超星尔雅网络课程编辑：程序博客网时间：2024/06/03 14:41

太感谢知乎的大牛了，看了他们聪明的解释之后，心里豁然开朗了，

原文：https://www.zhihu.com/question/22298352

从数学上讲，卷积就是一种运算，和加、减、乘、除一样，只是更抽象一点

卷积的重要的物理意义是：一个函数（如：单位响应）在另一个函数（如：输入信号）上的加权叠加。

下面是python 两种方法进行简单的卷积计算：

import numpy as npimport matplotlib.pyplot as plta=[1,2,3,4]b=[1,1,1]plt.plot(a)plt.plot(b)end=np.convolve(a,b,'full')print(end)plt.plot(end)# plt.show()import scipy.signalimport numpy as npx=np.array([1,2,3,4])h=np.array([1,1,1])bb= scipy.signal.convolve(x,h) #卷积运算print(bb)

作者：张俊博
链接：https://www.zhihu.com/question/22298352/answer/34267457
来源：知乎
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

有那么麻烦吗？
不推荐用“反转/翻转/反褶/对称”等解释卷积。好好的信号为什么要翻转？导致学生难以理解卷积的物理意义。
这个其实非常简单的概念，国内的大多数教材却没有讲透。

直接看图，不信看不懂。以离散信号为例，连续信号同理。

已知 $x[0] = a, x[1] = b, x[2]=c$
&amp;lt;img src="https://pic4.zhimg.com/50/153fd3e7911d486edaf0475afb1e54b3_hd.png" data-rawwidth="600" data-rawheight="214" class="origin_image zh-lightbox-thumb" width="600" data-original="https://pic4.zhimg.com/153fd3e7911d486edaf0475afb1e54b3_r.png"&amp;gt;

已知 $y[0] = i, y[1] = j, y[2]=k$
&amp;lt;img src="https://pic3.zhimg.com/50/c47d9d7f7a29c491782bf7b1baea3f8e_hd.png" data-rawwidth="600" data-rawheight="214" class="origin_image zh-lightbox-thumb" width="600" data-original="https://pic3.zhimg.com/c47d9d7f7a29c491782bf7b1baea3f8e_r.png"&amp;gt;

下面通过演示求 $x[n] * y[n]$ 的过程，揭示卷积的物理意义。

第一步， $x[n]$ 乘以 $y[0]$ 并平移到位置0：
&amp;lt;img src="https://pic1.zhimg.com/50/91f5eff235013ac729c44e98b3a537d0_hd.png" data-rawwidth="600" data-rawheight="214" class="origin_image zh-lightbox-thumb" width="600" data-original="https://pic1.zhimg.com/91f5eff235013ac729c44e98b3a537d0_r.png"&amp;gt;
第二步， $x[n]$ 乘以 $y[1]$ 并平移到位置1：
&amp;lt;img src="https://pic1.zhimg.com/50/67c05239b05f671766b9df9393026f2c_hd.png" data-rawwidth="600" data-rawheight="214" class="origin_image zh-lightbox-thumb" width="600" data-original="https://pic1.zhimg.com/67c05239b05f671766b9df9393026f2c_r.png"&amp;gt;
第三步， $x[n]$ 乘以 $y[2]$ 并平移到位置2：
&amp;lt;img src="https://pic2.zhimg.com/50/c34e839a49c6b616c57bde3c3dbbd67d_hd.png" data-rawwidth="600" data-rawheight="214" class="origin_image zh-lightbox-thumb" width="600" data-original="https://pic2.zhimg.com/c34e839a49c6b616c57bde3c3dbbd67d_r.png"&amp;gt;
最后，把上面三个图叠加，就得到了 $x[n] * y[n]$ ：
&amp;lt;img src="https://pic3.zhimg.com/50/4ce6cdcc28b10aca73db3f877d86ca02_hd.png" data-rawwidth="600" data-rawheight="313" class="origin_image zh-lightbox-thumb" width="600" data-original="https://pic3.zhimg.com/4ce6cdcc28b10aca73db3f877d86ca02_r.png"&amp;gt;

简单吧？无非是平移（没有反褶！）、叠加。

====================================================

从这里，可以看到卷积的重要的物理意义是：一个函数（如：单位响应）在另一个函数（如：输入信号）上的加权叠加。

重复一遍，这就是卷积的意义：加权叠加。

对于线性时不变系统，如果知道该系统的单位响应，那么将单位响应和输入信号求卷积，就相当于把输入信号的各个时间点的单位响应加权叠加，就直接得到了输出信号。

通俗的说：
在输入信号的每个位置，叠加一个单位响应，就得到了输出信号。
这正是单位响应是如此重要的原因。

在输入信号的每个位置，叠加一个单位响应，就得到了输出信号。
这正是单位响应是如此重要的原因。

复利计算：

可见，最终小明拿到的钱将等于他各年存入的钱分别计算复利之后得到的钱数的总和，即：
<noscript><img src="https://pic3.zhimg.com/50/fba65159d3472936979002b01b606a0e_hd.jpg" data-rawwidth="1077" data-rawheight="124" class="origin_image zh-lightbox-thumb" width="1077" data-original="https://pic3.zhimg.com/fba65159d3472936979002b01b606a0e_r.jpg">用求和符号来简化这个公式，可以得到：</noscript>

用求和符号来简化这个公式，可以得到：
$\sum_{i=0}^{5}{f(i)g(5-i)}, \mathrm{where} \ f(i)=100, g(5-i) = (1.05)^{5-i}$
在上式中， f(i) 为小明的存钱函数，而 g(i) 为存入银行的每一笔钱的复利计算函数。在这里，小明最终得到的钱就是他的存钱函数和复利计算函数的卷积。

显示完整版：

应题主邀，把我在卷积的物理意义是什么？ - 数学的答案搬过来。
——————————————————————————————————————
对于初学者，我推荐用复利的例子来理解卷积可能更好理解一些：

小明存入100元钱，年利率是5%，按复利计算（即将每一年所获利息加入本金，以计算下一年的利息），那么在五年之后他能拿到的钱数是 $100(1+5\%)^5$ ，如下表所示：
&amp;lt;img src="https://pic2.zhimg.com/50/5fa86c80c31dd277d038527555aa4d75_hd.jpg" data-rawwidth="1293" data-rawheight="95" class="origin_image zh-lightbox-thumb" width="1293" data-original="https://pic2.zhimg.com/5fa86c80c31dd277d038527555aa4d75_r.jpg"&amp;gt;将这笔钱存入银行的一年之后，小明又往银行中存入了100元钱，年利率仍为5%，那么这笔钱按复利计算，到了第五年，将收回的钱数是将这笔钱存入银行的一年之后，小明又往银行中存入了100元钱，年利率仍为5%，那么这笔钱按复利计算，到了第五年，将收回的钱数是 $100(1+5\%)^4$ ，我们将这一结果作为新的一行加入上面的表格中：
&amp;lt;img src="https://pic4.zhimg.com/50/39f37df8c96d7219cba5d081919a3a2f_hd.jpg" data-rawwidth="1296" data-rawheight="134" class="origin_image zh-lightbox-thumb" width="1296" data-original="https://pic4.zhimg.com/39f37df8c96d7219cba5d081919a3a2f_r.jpg"&amp;gt;以此类推，如果小明每年都往银行中存入新的100元钱，那么这个收益表格将是这样的：以此类推，如果小明每年都往银行中存入新的100元钱，那么这个收益表格将是这样的：
&amp;lt;img src="https://pic2.zhimg.com/50/cfe98b9d33640fae02a21bf369f0459d_hd.jpg" data-rawwidth="1296" data-rawheight="284" class="origin_image zh-lightbox-thumb" width="1296" data-original="https://pic2.zhimg.com/cfe98b9d33640fae02a21bf369f0459d_r.jpg"&amp;gt;可见，最终小明拿到的钱将等于他各年存入的钱分别计算复利之后得到的钱数的总和，即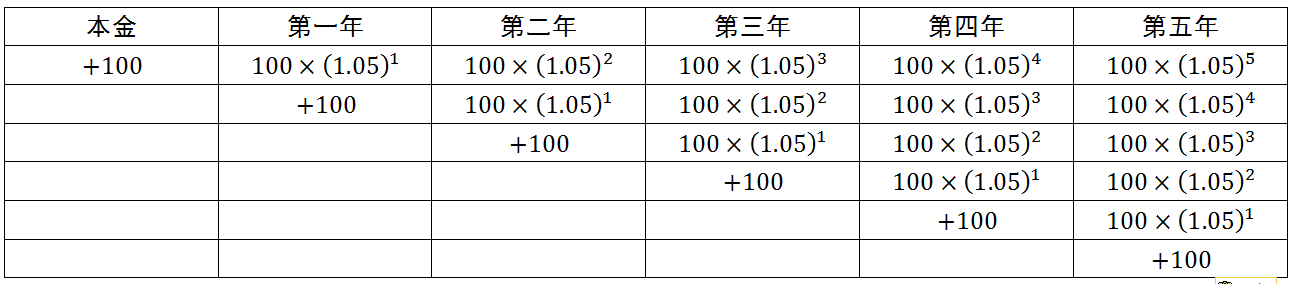：可见，最终小明拿到的钱将等于他各年存入的钱分别计算复利之后得到的钱数的总和，即：
&amp;lt;img src="https://pic3.zhimg.com/50/fba65159d3472936979002b01b606a0e_hd.jpg" data-rawwidth="1077" data-rawheight="124" class="origin_image zh-lightbox-thumb" width="1077" data-original="https://pic3.zhimg.com/fba65159d3472936979002b01b606a0e_r.jpg"&amp;gt;用求和符号来简化这个公式，可以得到：

用求和符号来简化这个公式，可以得到：
$\sum_{i=0}^{5}{f(i)g(5-i)}, \mathrm{where} \ f(i)=100, g(5-i) = (1.05)^{5-i}$
在上式中， $f(i)$ 为小明的存钱函数，而 $g(i)$ 为存入银行的每一笔钱的复利计算函数。在这里，小明最终得到的钱就是他的存钱函数和复利计算函数的卷积。
为了更清晰地看到这一点，我们将这个公式推广到连续的情况，也就是说，小明在从 $0$ 到 $t$ 的这一段时间内，每时每刻都往银行里存钱，他的存钱函数为 $f(\tau)\ (0\leq \tau\leq t)$ ，而银行也对他存入的每一笔钱按复利公式计算收益： $g(t-\tau)=(1+5\%)^{t-\tau}$ ，则小明到时间 $t$ 将得到的总钱数为：
$\int_{0}^{t} f(\tau)g(t-\tau)d\tau=\int_{0}^{t} f(\tau)(1+5\%)^{t-\tau}d\tau$
这也就是卷积的表达式了，上式可以记为 $(f\ast g)(t)$ 。

相信通过上面这个例子，大家应该能够很清晰地记住卷积公式了。下面我们再展开说两句：
如果我们将小明的存款函数视为一个信号发生（也就是激励）的过程，而将复利函数 $g(t-\tau)$ 视为一个系统对信号的响应函数（也就是响应），那么二者的卷积 $(f\ast g)(t)$ 就可以看做是在 $t$ 时刻对系统进行观察，得到的观察结果（也就是输出）将是过去产生的所有信号经过系统的「处理／响应」后得到的结果的叠加，这也就是卷积的物理意义了。

掷骨子：

把这两枚骰子都抛出去，两个骰子加起来要等于4的概率是多少？

这正是卷积的应用场景

符合卷积的定义，把它写成标准的形式就是：

$\displaystyle (f*g)(4)=\sum _{m=1}^{3}f(4-m)g(m)$

阅读全文

0 0