547. Friend Circles问题深入分析

声明：本文中代码来自于https://leetcode.com/problems/friend-circles/discuss/中的[C++] Clean Code - DFS|UnionFind，本文仅仅阐释我对这段代码的理解。

题目：

There are N students in a class. Some of them are friends, while some are not. Their friendship is transitive in nature. For example, if A is adirect friend of B, and B is adirect friend of C, then A is anindirect friend of C. And we defined a friend circle is a group of students who are direct or indirect friends.

Given a N*N matrix M representing the friend relationship between students in the class. If M[i][j] = 1, then the i_th and j_th students are direct friends with each other, otherwise not. And you have to output the total number of friend circles among all the students.

翻译：用图的邻接矩阵表示每个人之间的朋友关系，如果M[i][j] = 1,表示 i 和 j 具有朋友关系，朋友关系具有传递性，朋友关系的人们形成朋友圈，求出朋友圈的个数。

Example 1:

Input: [[1,1,0], [1,1,0], [0,0,1]]Output: 2Explanation:The 0th and 1st students are direct friends, so they are in a friend circle. The 2nd student himself is in a friend circle. So return 2.

Example 2:

Input: [[1,1,0], [1,1,1], [0,1,1]]Output: 1Explanation:The 0th and 1st students are direct friends, the 1st and 2nd students are direct friends, so the 0th and 2nd students are indirect friends. All of them are in the same friend circle, so return 1.

Note:

1. N is in range [1,200].
2. M[i][i] = 1 for all students.
3. If M[i][j] = 1, then M[j][i] = 1.

给出程序实现的接口如下：

class Solution {
public:
    int findCircleNum(vector<vector<int>>& M) {
       
    }
};

开始你的表演。

---------------------------------------------------------------------------------------------------------------------

分析：

这里的朋友关系实际上是一种具有自反性，对称性，传递性的等价关系，利用它可以对整个朋友集合进行分类，从而形成所谓的朋友圈（离散数学角度）

那么，相对于图来说，这种划分实际上叫做连通分支。

连通分支定义：

根据定义可见，如果x，y，z都是拓扑空间X中的点，则

（1）x和x连通（因为每一个单点集都是连通子集）；

（2）如果x和y连通，则y和x也连通；（显然）

（3）如果x和y连通，并且y和z连通，则x和z连通．（这是因为，这时存在X中的连通子集A和B使得x，y∈A和y，z∈B．从而由于y∈A∩B可见A∪B连通，并且x，z∈A∪B．因此x和z连通）

那么本题目实质是问求连通分支的个数的方法是什么。

图的BFS（或者DFS）遍历
定义visited参考矩阵，visited[i]表示该节点是否被遍历到，从visited[0],即第一个节点开始，如果遇到没有被遍历到的节点就对该节点进行BFS遍历，直到达到visited数组的尽头。
中途记录调用BFS的次数即为连通分支的个数，下面的解法使用的是DFS遍历。 

1.只关心朋友圈的个数，不关心每个朋友圈里面的朋友个数和具体朋友对象是谁。

class Solution {
public:
    int findCircleNum(vector<vector<int>>& M){
        if (M.empty()) return 0;
        int n = M.size();
        vector<bool> visited(n,false);
        int groups = 0;
        for (int i =0; i < visited.size(); i++) {
            groups += !visited[i] ? dfs(i, M, visited), 1 : 0;
        }
        return groups;
    }

private:
    void dfs(int i, vector<vector<int>>& M,vector<bool>& visited){
        visited[i] = true;
        for (int j =0; j < visited.size(); j++) {
            if (i != j && M[i][j] && !visited[j]) {
                dfs(j, M, visited);
            }
        }
    }
};

采用了广度优先遍历，从每个点出发去寻找邻接的点，

如果某一个点和其他点之间可达（具有了朋友关系），那么从该点可以进入一个连通分支，则其他点的访问标识=1，

如果这个点没有被访问，则从它开始访问其他点，观察是否存在连通分支，这个点是连通分支的一个入口。

2.关心朋友圈的个数和每个朋友圈里面的人数

对dfs加入返回值返回成员的个数，dfs函数内部加入记录变量记录该连通分支里面的成员的个数。

class Solution {
public:
    int findCircleNum(vector<vector<int>>& M) {
        if (M.empty()) return 0;
        int n = M.size();
        vector<bool> visited(n, false);
        int groups = 0;
        for (int i = 0; i < visited.size(); i++) {
            groups += dfs(i, M, visited) > 0;

            //dfs(i, M, visited)的返回值是该组连通分支的成员个数
        }
        return groups;
    }

private:
    int dfs(int i, vector<vector<int>>& M, vector<bool>& visited) {
        if (visited[i]) {
            return 0;
        }

        int ppl = 1;
        visited[i] = true;
        for (int j = 0; j < visited.size(); j++) {
            if (i != j && M[i][j]) {
                ppl += dfs(j, M, visited);
            }
        }

        return ppl;
    }
};

3.关心朋友圈的个数，朋友圈里面的成员和成员个数

class Solution {
public:
 int findCircleNum(vector<vector<int>>& M) {
  if (M.empty()) return 0;
  int n = M.size();
  vector<bool> visited(n, false);
  int groups = 0;
  for (int i = 0; i < visited.size(); i++) {
   vector<int> cycle_content;
   int cycle_number = dfs(i, M, visited,cycle_content);
   if (cycle_number>0)
   {
    cout << "cycle_number:"<< cycle_number << endl;
    cout << "cycle_content:" << endl;
    for (int i:cycle_content)
    {
     cout << i << endl;
    }
   }
   cycle_content.clear();
   //这里的cycle_number为该环里面的元素个数
   groups += cycle_number > 0;
  }
  return groups;
 }
private:
 int dfs(int i, vector<vector<int>>& M, vector<bool>& visited, vector<int>& cycle_content) {
  /*深度优先访问到i结点，如果i结点被访问了，则不计入成员的个数，如果没有访问则当前连通分支的成员个数 = 1 + 和它相连的结点形成的连通分支的成员个数。这里visited的格式很重要，通过引用的方式能够把访问的情况及时传递给接下来的访问动作从而能够保证在深度优先遍历过程中及时向后续的DFS传递想要的结果 */
  if (visited[i]) {
   return 0;
  }
  int ppl = 1;/* 当前的成员的个数*/
  visited[i] = true;
  cycle_content.push_back(i);
  for (int j = 0; j < visited.size(); j++) {
   if (i != j && M[i][j]) {
    ppl += dfs(j, M, visited,cycle_content);
   }
  }
  return ppl;
 }
};

4.并查集的应用

并查集是一种树型的数据结构，使用并查集主要是处理一些不相交集合（Disjoint Sets）的合并及查询问题。

常常在使用中以森林来表示。

并就是按一定顺序将属于同一组的元素所在的集合合并。

查就是查找一个元素在哪个集合中。

并查集就是具备合并和查找功能的集合描述形式。

并查集的主要操作：

1、初始化：把每个点所在集合初始化为其自身；

2、查找：查找元素所在的集合即根节点；

3、合并：将两个元素所在的集合合并为一个集合，合并两个不相交集合判断两个元素是否属于同一集合。

并查集的时间复杂度

并查集进行n次查找的时间复杂度是O(n )（执行n-1次合并和m≥n次查找）。其中 是一个增长极其缓慢的函数，它是阿克曼函数（Ackermann Function）的某个反函数。它可以看作是小于5的。所以可以认为并查集的时间复杂度几乎是线性的。

关于并查集的原理，可以出门左拐找这个，很细致很生动有趣的一篇博文。

http://blog.csdn.net/jinzk123/article/details/52231178

以下部分为全文引用。

为了解释并查集的原理，我举一个生动的例子。

话说江湖上散落着各式各样的大侠，有上千个之多。他们没有什么正当职业，整天背着剑在外面走来走去，碰到和自己不是一路人的，就免不了要打一架。但大侠们有一个优点就是讲义气，绝对不打自己的朋友。而且他们信奉“朋友的朋友就是我的朋友”，只要是能通过朋友关系串联起来的，不管拐了多少个弯，都认为是自己人。这样一来，江湖上就形成了一个一个的群落，通过两两之间的朋友关系串联起来。而不在同一个群落的人，无论如何都无法通过朋友关系连起来，于是就可以放心往死了打。但是两个原本互不相识的人，如何判断是否属于一个朋友圈呢？

我们可以在每个朋友圈内推举出一个比较有名望的人，作为该圈子的代表人物，这样，每个圈子就可以这样命名“齐达内朋友之队”“罗纳尔多朋友之队”……两人只要互相对一下自己的队长是不是同一个人，就可以确定敌友关系了。

但是还有问题啊，大侠们只知道自己直接的朋友是谁，很多人压根就不认识队长，要判断自己的队长是谁，只能漫无目的的通过朋友的朋友关系问下去：“你是不是队长？你是不是队长？”这样一来，队长面子上挂不住了，而且效率太低，还有可能陷入无限循环中。于是队长下令，重新组队。队内所有人实行分等级制度，形成树状结构，我队长就是根节点，下面分别是二级队员、三级队员。每个人只要记住自己的上级是谁就行了。遇到判断敌友的时候，只要一层层向上问，直到最高层，就可以在短时间内确定队长是谁了。由于我们关心的只是两个人之间是否连通，至于他们是如何连通的，以及每个圈子内部的结构是怎样的，甚至队长是谁，并不重要。所以我们可以放任队长随意重新组队，只要不搞错敌友关系就好了。于是，门派产生了。

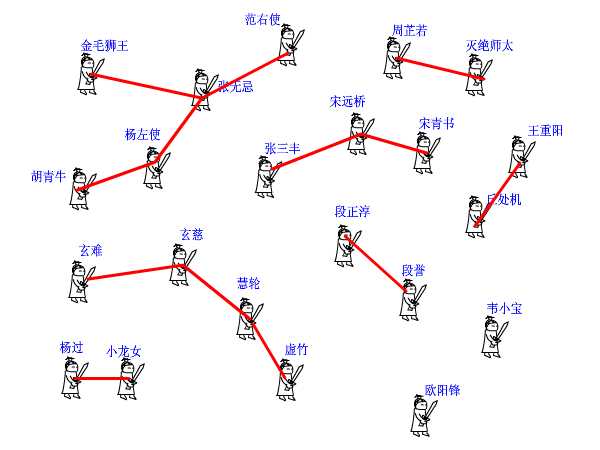
下面我们来看并查集的实现。 int pre[1000]; 这个数组，记录了每个大侠的上级是谁。大侠们从1或者0开始编号（依据题意而定），pre[15]=3就表示15号大侠的上级是3号大侠。如果一个人的上级就是他自己，那说明他就是掌门人了，查找到此为止。也有孤家寡人自成一派的，比如欧阳锋，那么他的上级就是他自己。每个人都只认自己的上级。比如胡青牛同学只知道自己的上级是杨左使。张无忌是谁？不认识！要想知道自己的掌门是谁，只能一级级查上去。 find这个函数就是找掌门用的，意义再清楚不过了（路径压缩算法先不论，后面再说）。

int find(int x)                                                                  //查找我（x）的掌门

{

    int r=x;                                                                       //委托 r 去找掌门

    while (pre[r ]!=r)                                                        //如果r的上级不是r自己（也就是说找到的大侠他不是掌门 = =）

    r=pre[r ] ;                                                                   // r 就接着找他的上级，直到找到掌门为止。

    return  r ;                                                                   //掌门驾到~~~

}

再来看看join函数，就是在两个点之间连一条线，这样一来，原先它们所在的两个板块的所有点就都可以互通了。这在图上很好办，画条线就行了。但我们现在是用并查集来描述武林中的状况的，一共只有一个pre[]数组，该如何实现呢？ 还是举江湖的例子，假设现在武林中的形势如图所示。虚竹小和尚与周芷若MM是我非常喜欢的两个人物，他们的终极boss分别是玄慈方丈和灭绝师太，那明显就是两个阵营了。我不希望他们互相打架，就对他俩说：“你们两位拉拉勾，做好朋友吧。”他们看在我的面子上，同意了。这一同意可非同小可，整个少林和峨眉派的人就不能打架了。这么重大的变化，可如何实现呀，要改动多少地方？其实非常简单，我对玄慈方丈说：“大师，麻烦你把你的上级改为灭绝师太吧。这样一来，两派原先的所有人员的终极boss都是师太，那还打个球啊！反正我们关心的只是连通性，门派内部的结构不要紧的。”玄慈一听肯定火大了：“我靠，凭什么是我变成她手下呀，怎么不反过来？我抗议！”抗议无效，上天安排的，最大。反正谁加入谁效果是一样的，我就随手指定了一个。这段函数的意思很明白了吧？

void join(int x,int y)                                                                   //我想让虚竹和周芷若做朋友

{

    int fx=find(x),fy=find(y);                                                       //虚竹的老大是玄慈，芷若MM的老大是灭绝

    if(fx!=fy)                                                                               //玄慈和灭绝显然不是同一个人

    pre[fx ]=fy;                                                                           //方丈只好委委屈屈地当了师太的手下啦

}

再来看看路径压缩算法。建立门派的过程是用join函数两个人两个人地连接起来的，谁当谁的手下完全随机。最后的树状结构会变成什么胎唇样，我也完全无法预计，一字长蛇阵也有可能。这样查找的效率就会比较低下。最理想的情况就是所有人的直接上级都是掌门，一共就两级结构，只要找一次就找到掌门了。哪怕不能完全做到，也最好尽量接近。这样就产生了路径压缩算法。 设想这样一个场景：两个互不相识的大侠碰面了，想知道能不能揍。 于是赶紧打电话问自己的上级：“你是不是掌门？” 上级说：“我不是呀，我的上级是谁谁谁，你问问他看看。” 一路问下去，原来两人的最终boss都是东厂曹公公。 “哎呀呀，原来是记己人，西礼西礼，在下三营六组白面葫芦娃!” “幸会幸会，在下九营十八组仙子狗尾巴花！” 两人高高兴兴地手拉手喝酒去了。 “等等等等，两位同学请留步，还有事情没完成呢！”我叫住他俩。 “哦，对了，还要做路径压缩。”两人醒悟。 白面葫芦娃打电话给他的上级六组长：“组长啊，我查过了，其习偶们的掌门是曹公公。不如偶们一起及接拜在曹公公手下吧，省得级别太低，以后查找掌门麻环。” “唔，有道理。” 白面葫芦娃接着打电话给刚才拜访过的三营长……仙子狗尾巴花也做了同样的事情。 这样，查询中所有涉及到的人物都聚集在曹公公的直接领导下。每次查询都做了优化处理，所以整个门派树的层数都会维持在比较低的水平上。路径压缩的代码，看得懂很好，看不懂也没关系，直接抄上用就行了。总之它所实现的功能就是这么个意思（找到u所在树的根v以后，把从u到v的路径上所有点的父亲都设置为v，减少之后再查找操作的查找次数）。

据此，并查集实现查找连通分支的代码如下：

class Solution {
public:
    int findCircleNum(vector<vector<int>>& M) {
        if (M.empty()) return 0;
        int n = M.size();

        vector<int> leads(n, 0);
        for (int i = 0; i < n; i++) { leads[i] = i; }   // initialize leads for every kid as themselves

        int groups = n;
        for (int i = 0; i < n; i++) {
            for (int j = i + 1; j < n; j++) {   // avoid recalculate M[i][j], M[j][i]
                if (M[i][j]) {//实现的是join功能，将两个元素合并到一棵树上，同时计数器减去1，这里并没有实现路径压缩功能，因为数据量不大，另外可能代码作者也觉得麻烦没做。
                    int lead1 = find(i, leads);
                    int lead2 = find(j, leads);
                    if (lead1 != lead2) {       // if 2 group belongs 2 different leads, merge 2 group to 1
                        leads[lead1] = lead2;
                        groups--;
                    }
                }
            }
        }
        return groups;
    }

private:
    int find(int x, vector<int>& parents) {//实现的是find功能，查找祖先结点是什么
        return parents[x] == x ? x : find(parents[x], parents);
    }
};

可以看到，这里用的其实就是join集合合并操作，将每个节点视为一个独立的集合，然后做集合的合并，合并的过程会调用查找的过程，从而实现并查集对于不相交集合的合并操作（符合一定条件时执行合并操作，这个条件就是题目中的连通，可达的这一等价关系）。

其实路径压缩是可以在find里面做的，按照那篇并查集的博文所述，这里的find可以稍作修改。

   int find(int x, vector<int>& parents) {//实现的是find功能，查找祖先结点是什么
        int root=(parents[x] == x ? x : find(parents[x], parents));
        int j;//完成了找到根结点之后，进行一下路径压缩
         while(x!=root)
         {        //每次找到了root结点之后都把新节点放进root结点的孩子里面去，对新节点的父结点也这样做
             j=parents[x];//保存x结点的父结点
             parents[x]=root;//x结点的父结点改成root结点
             x=j;//对x的父结点也做这样的更改，直到父结点就是root结点为止
        }
        return root;
    }

 路径压缩的方法是多种多样的了，这里用的是最简单的压缩方法了。

压缩路径可以有很多种方法，这里介绍两种最常用的方法：
（1）满路径压缩（full compresses paths）：这是一种极其简单但又很常用的方法。就是在添加另一个集合的时候，把所有遇到的结点都指向根节点，也就是我们上面用到的压缩方法。
（2）二分压缩路径（compresses paths by halving）：具体思想就是把当前的结点，跳过一个指向父亲的父亲，从而使整个路径减半深度减半。这种办法比满路径压缩要快那么一点点。数据越大，当然区别就会越明显。
压缩路径的本质使路径深度更加地减小，从而使访问的时候速度增快，是一种很不错的优化。在使用路径压缩以后，由于深度经常性发生变化，因此我们不再使用深度作为合并操作的启发式函数值，而是使用一个新的rank数。刚建立的新集合的rank为0，以后当两个rank相同的树合并时，随便选一棵树作为新根，并把它的rank加1；否则rank大的树作为新根，两棵树的rank均不变。