TRPO

来源：互联网发布：js 拖动事件编辑：程序博客网时间：2024/06/16 20:21

转载自知乎专栏天津包子馅儿的知乎

今天开始我们的第七讲，TRPO。先简短地介绍一下：TRPO是英文单词Trust region policy optimization的简称，翻译成中文是信赖域策略优化。提出这个算法的人是伯克利的博士生John Schulman，此人已于2016年博士毕业。Schulman的导师是强化学习领域的大神Pieter Abbeel, Abbeel是伯克利的副教授，同时也是OpenAI的研究科学家，是机器人强化学习领域最有影响力的人之一。

如果进一步追根溯源的话，Abbeel毕业于斯坦福大学，导师是Andrew Ng（吴恩达）。相信搞机器学习的人应该都听说过此大神或者听过他的课吧。有意思的是，吴恩达博士毕业于伯克利，之后在斯坦福任教，这跟Abbeel的经历正好相反。看来美国名校间人才互换的情况还是挺普遍的。Abbeel博士做的课题是逆向强化学习（学徒学习）。如果再进一步追根溯源，吴恩达的导师是伯克利的Michael I. Jordan，一个将统计学和机器学习联合起来的大师级人物……

扯的好像有点多了，其实不然。说那么多其实跟今天的主题有关系。从师承关系我们可以看到，这个学派由统计学大师Michael I. Jordan传下来，所以他们最有力的杀手锏是统计学习。从宏观意义上来讲，TRPO将统计玩到了一个新高度。在TRPO出来之前，大部分强化学习算法很难保证单调收敛，而TRPO却给出了一个单调的策略改善方法。所以，不管你从事什么行业，想用强化学习解决你的问题，TRPO是一个不错的选择。所以，这一节，很关键。好了，现在我们正式进入这一讲。

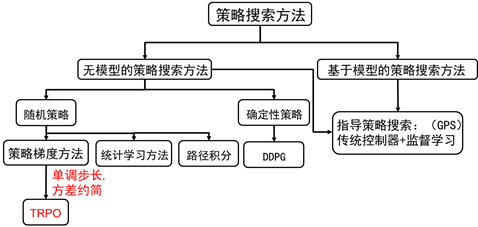
图7.1 策略搜索方法分类

策略梯度的缺点

上一节，我们已经讲了策略梯度的方法。当然策略梯度方法博大精深，上一讲只是给出一个入门的介绍，在策略梯度方法中还有很多有意思的课题，比如相容函数法，自然梯度法等等。但Shulman在博士论文中已证明，这些方法其实都是TRPO弱化的特例，说这些是再次强调TRPO的强大之处。

我们知道，根据策略梯度方法，参数更新方程式为：

$\theta_{new}=\theta_{old}+\alpha\nabla_{\theta}J$ （7.1）

策略梯度算法的硬伤就在更新步长 $\alpha$ ，当步长不合适时，更新的参数所对应的策略是一个更不好的策略，当利用这个更不好的策略进行采样学习时，再次更新的参数会更差，因此很容易导致越学越差，最后崩溃。所以，合适的步长对于强化学习非常关键。

什么叫合适的步长？

所谓合适的步长是指当策略更新后，回报函数的值不能更差。如何选择这个步长？或者说，如何找到新的策略使得新的回报函数的值单调增，或单调不减。这是TRPO要解决的问题。

用 $\tau$ 表示一组状态-行为序列 $s_0,u_0,\cdots ,s_H,u_H$ ，强化学习的回报函数为：

$\eta\left(\tilde{\pi}\right)=E_{\tau |\tilde{\pi}}\left[\sum_{t=0}^{\infty}{\gamma^t\left(r\left(s_t\right)\right)}\right]$

这里，我们用 $\tilde{\pi}$ 表示策略。

刚才已经说过，TRPO是找到新的策略，使得回报函数单调不减，一个自然地想法是能不能将新的策略所对应的回报函数分解成旧的策略所对应的回报函数+其他项。只要新的策略所对应的其他项大于等于零，那么新的策略就能保证回报函数单调不减。其实是存在这样的等式，这个等式是2002年Sham Kakade提出来的。TRPO的起点便是这样一个等式：

$\eta\left(\tilde{\pi}\right)=\eta\left(\pi\right)+E_{s_0,a_0,\cdots ~\tilde{\pi}}\left[\sum_{t=0}^{\infty}{\gamma^tA_{\pi}\left(s_t,a_t\right)}\right]$ (7.2)

这里我们用 $\pi$ 表示旧的策略，用 $\tilde{\pi}$ 表示新的策略。其中， $A_{\pi}\left(s,a\right)=Q_{\pi}\left(s,a\right)-V_{\pi}\left(s\right)\]\[=E_{s'~P\left(s'|s,a\right)}\left[r\left(s\right)+\gamma V^{\pi}\left(s'\right)-V^{\pi}\left(s\right)\right]$

称为优势函数。

此处我们再花点笔墨介绍下 $Q_{\pi}\left(s,a\right)-V_{\pi}\left(s\right)$ 为什么称为优势函数，这个优势到底跟谁比。还是以大家熟悉的树状图来讲解：

图7.2 优势函数示意图

如图7.2，值函数 $V(s)$ 可以理解为在该状态 $S$ 下所有可能动作所对应的动作值函数乘以采取该动作的概率的和。更通俗的讲，值函数 $V(S)$ 是该状态下所有动作值函数关于动作概率的平均值。而动作值函数 $Q(s,a)$ 是单个动作所对应的值函数， $Q_{\pi}\left(s,a\right)-V_{\pi}\left(s\right)$ 能评价当前动作值函数相对于平均值的大小。所以，这里的优势指的是动作值函数相比于当前状态的值函数的优势。如果优势函数大于零，则说明该动作比平均动作好，如果优势函数小于零，则说明当前动作还不如平均动作好。

回到正题上来，我们给出公式（7.2）的证明：

证明：

$E_{\tau |\tilde{\pi}}\left[\sum_{t=0}^{\infty}{\gamma^tA_{\pi}\left(s_t,a_t\right)}\right]\]\[=E_{\tau |\tilde{\pi}}\left[\sum_{t=0}^{\infty}{\gamma^t\left(r\left(s\right)+\gamma V^{\pi}\left(s_{t+1}\right)-V^{\pi}\left(s_t\right)\right)}\right]\]\[=E_{\tau |\tilde{\pi}}\left[\sum_{t=0}^{\infty}{\gamma^t\left(r\left(s_t\right)\right)+\sum_{t=0}^{\infty}{\gamma^t\left(\gamma V^{\pi}\left(s_{t+1}\right)-V^{\pi}\left(s_t\right)\right)}}\right]\]\[=E_{\tau |\tilde{\pi}}\left[\sum_{t=0}^{\infty}{\gamma^t\left(r\left(s_t\right)\right)}\right]+E_{s_0}\left[-V^{\pi}\left(s_0\right)\right]\]\[=\eta\left(\tilde{\pi}\right)-\eta\left(\pi\right)$

我们详细讲解一下：

第一个等号是将优势函数的定义带入。

第二个等号是把第一项和后两项分开来写。

第三个等号是将第二项写开来，相消，只剩 $-V^{\pi}\left(s_0\right)$ ，而 $s_0 \sim \tilde{\pi}$
等价于 $s_0 \sim \pi$ ，因为两个策略都从同一个初始状态开始。而 $V^{\pi}\left(s_0\right)=\eta\left(\pi\right)$

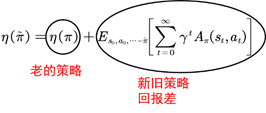
图7.3 TRPO最重要的等式

为了在等式（7.2）中出现策略项，我们需要对公式（7.2）进一步加工转化。如图7.3，我们对新旧策略回报差进行转化。优势函数的期望可以写成如下式：

$\eta\left(\tilde{\pi}\right)=\eta\left(\pi\right)+\sum_{t=0}^{\infty}{\sum_s{P\left(s_t=s|\tilde{\pi}\right)}}\sum_a{\tilde{\pi}\left(a|s\right)\gamma^tA_{\pi}\left(s,a\right)}$ (7.3)

其中 $P\left(s_t=s|\tilde{\pi}\right)\tilde{\pi}\left(a|s\right)$ 为 $(s,a)$ 的联合概率， $\sum_a{\tilde{\pi}\left(a|s\right)\gamma^tA_{\pi}\left(s,a\right)}$ 为求对动作a的边际分布，也就是说在状态s对整个动作空间求和； $\sum_s{P\left(s_t=s|\tilde{\pi}\right)}$ 为求对状态s的边际分布，即对整个状态空间求和； $\sum_{t=0}^{\infty}{\sum_s{P\left(s_t=s|\tilde{\pi}\right)}}$ 求整个时间序列的和。

我们定义 $\rho_{\pi}\left(s\right)=P\left(s_0=s\right)+\gamma P\left(s_1=s\right)+\gamma^2P\left(s_2=s\right)+\cdots$

则：

$\eta\left(\tilde{\pi}\right)=\eta\left(\pi\right)+\sum_s{\rho_{\tilde{\pi}}\left(s\right)\sum_a{\tilde{\pi}\left(a|s\right)A^{\pi}\left(s,a\right)}}$ (7.4)

如图所示：

图7.4 代价函数推导

注意，这时状态s的分布由新的策略产生，对新的策略严重依赖。

TRPO第一个技巧

这时，我们引入TRPO的第一个技巧对状态分布进行处理。我们忽略状态分布的变化，依然采用旧的策略所对应的状态分布。这个技巧是对原代价函数的第一次近似。其实，当新旧参数很接近时，我们将用旧的状态分布代替新的状态分布也是合理的。这时，原来的代价函数变成了：

$L_{\pi}\left(\tilde{\pi}\right)=\eta\left(\pi\right)+\sum_s{\rho_{\pi}\left(s\right)\sum_a{\tilde{\pi}\left(a|s\right)A^{\pi}\left(s,a\right)}}$ (7.5)

我们再看(7.5)式的第二项策略部分，这时的动作a是由新的策略 $\tilde{\pi}$ 产生。可是新的策略 $\tilde{\pi}$ 是带参数 $\theta$ 的，这个参数是未知的，因此无法用来产生动作。这时，我们引入TRPO的第二个技巧。

TRPO第二个技巧

TRPO的第二个技巧是利用重要性采样对动作分布进行的处理。

$\sum_a{\tilde{\pi}_{\theta}\left(a|s_n\right)A_{\theta_{old}}\left(s_n,a\right)=E_{a~q}\left[\frac{\tilde{\pi}_{\theta}\left(a|s_n\right)}{q\left(a|s_n\right)}A_{\theta_{old}}\left(s_n,a\right)\right]}$

通过利用两个技巧，我们再利用 $\frac{1}{1-\gamma}E_{s~\rho_{\theta_{old}}}\left[\cdots\right]$ 代替 $\sum_s{\rho_{\theta_{old}}\left(s\right)}\left[\cdots\right]$ ；取 $q\left(a|s_n\right)=\pi_{\theta_{old}}\left(a|s_n\right)$ ；

替代回报函数变为：

$L_{\pi}\left(\tilde{\pi}\right)=\eta\left(\pi\right)+E_{s~\rho_{\theta_{old}},a~\pi_{\theta_{old}}}\left[\frac{\tilde{\pi}_{\theta}\left(a|s\right)}{\pi_{\theta_{old}}\left(a|s\right)}A_{\theta_{old}}\left(s,a\right)\right]$ (7.6)

接下来，我们看一下替代回报函数（7.6）和原回报函数（7.4）有什么关系

通过比较我们发现，（7.4）和（7.6）唯一的区别是状态分布的不同。将 $L_{\pi}\left(\tilde{\pi}\right)\textrm{，}\eta\left(\tilde{\pi}\right)$ 都看成是策略 $\tilde{\pi}$ 的函数，则 $L_{\pi}\left(\tilde{\pi}\right)\textrm{，}\eta\left(\tilde{\pi}\right)$ 在策略 $\pi_{\theta_{old}}$ 处一阶近似，即：

$L_{\pi_{\theta_{old}}}\left(\pi_{\theta_{old}}\right)=\eta\left(\pi_{\theta_{old}}\right)\]\[\nabla_{\theta}L_{\pi_{\theta_{old}}}\left(\pi_{\theta}\right)|_{\theta =\theta_{old}}=\nabla_{\theta}\eta\left(\pi_{\theta}\right)|_{\theta =\theta_{old}}$ (7.7)

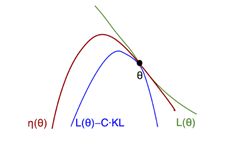
用图来表示为：

图7.5 回报函数与替代回报函数示意图

在 $\theta_{old}$ 附近，能改善L的策略也能改善原回报函数。问题是步长多大呢？

再次引入第二个重量级的不等式

$\eta\left(\tilde{\pi}\right)\geqslant L_{\pi}\left(\tilde{\pi}\right)-CD_{KL}^{\max}\left(\pi ,\tilde{\pi}\right)\textrm{，}\]\[where\ C=\frac{2\varepsilon\gamma}{\left(1-\gamma\right)^2}$ (7.8)

为了保持连贯性，该不等式的证明略，以后再专门开篇帖子补上。其中 $D_{KL}\left(\pi ,\tilde{\pi}\right)$ 是两个分布的KL散度。我们在这里看一看，该不等式给了我们什么启示。

首先，该不等式给了 $\eta\left(\tilde{\pi}\right)$ 的下界，我们定义这个下界为 $M_i\left(\pi\right)=L_{\pi_i}\left(\pi\right)-CD_{KL}^{\max}\left(\pi_i,\pi\right)$ ，

下面利用这个下界，我们证明策略的单调性： $\eta\left(\pi_{i+1}\right)\geqslant M_i\left(\pi_{i+1}\right)$

且 $\eta\left(\pi_i\right)=M_i\left(\pi_i\right)$

则： $\eta\left(\pi_{i+1}\right)-\eta\left(\pi_i\right)\geqslant M_i\left(\pi_{i+1}\right)-M\left(\pi_i\right)$

如果新的策略 $\pi_{i+1}$ 能使得 $M_i$ 最大，那么有不等式 $M_i\left(\pi_{i+1}\right)-M\left(\pi_i\right)\geqslant 0$ ，则 $\eta\left(\pi_{i+1}\right)-\eta\left(\pi_i\right)\geqslant 0$ ，这个使得 $M_i$ 最大的新的策略就是我们一直在苦苦找的要更新的策略。那么这个策略如何得到呢？

该问题可形式化为：

$maximize _{\theta}\left[L_{\theta_{old}}\left(\theta\right)-CD_{KL}^{\max}\left(\theta_{old},\theta\right)\right]$

如果利用惩罚因子C则每次迭代步长很小，因此问题可转化为：

$maximize_{\theta}E_{s\sim\rho_{\theta_{old}},a\sim\pi_{\theta_{old}}}\left[\frac{\pi_{\theta}\left(a|s\right)}{\pi_{\theta_{old}}\left(a|s\right)}A_{\theta_{old}}\left(s,a\right)\right]\]\[subject\ to\\ D_{KL}^{\max}\left(\theta_{old},\theta\right)\le\delta$ (7.9)

需要注意的是，因为有无穷多的状态，因此约束条件 $D_{KL}^{\max}\left(\theta_{old},\theta\right)$ 有无穷多个。问题不可解。

TRPO第三个技巧

在约束条件中，利用平均KL散度代替最大KL散度，即： $subject\ to \bar{D}_{KL}^{\rho_{\theta_{old}}}\left(\theta_{old},\theta\right)\le\delta$

TRPO第四个技巧：

$s \sim \rho_{\theta_{old}}\rightarrow s \sim \pi_{\theta_{old}}$

最终TRPO问题化简为：

$maximize_{\theta}E_{s\sim\pi_{\theta_{old}},a\sim\pi_{\theta_{old}}}\left[\frac{\pi_{\theta}\left(a|s\right)}{\pi_{\theta_{old}}\left(a|s\right)}A_{\theta_{old}}\left(s,a\right)\right]\]\[subject\ to\ E_{s \sim\pi_{\theta_{old}}}\left[D_{KL}\left(\pi_{\theta_{old}}\left(\cdot |s\right)||\pi_{\theta}\left(\cdot |s\right)\right)\right]\le\delta$ (7.10)

接下来就是利用采样得到数据，然后求样本均值，解决优化问题即可。至此，TRPO理论算法完成。关于如何求解，以及如何减小方差，我们之后的课程会再讲。

阅读全文

0 0