凸优化中的基本概念
来源:互联网 发布:js阻止a标签1次跳转 编辑:程序博客网 时间:2024/04/28 19:58
1.1 什么是凸集?
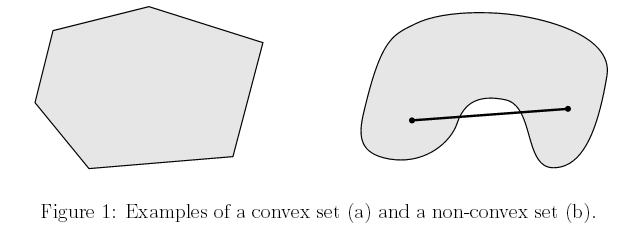
简单来说, 凸集是一个点集, 这个点集有一个性质, 就是在这个集合中任取不同的两个点x和y, 他们之间的线段(包括端点)上的点都属于这个点集,那么就说这个点集是一个凸集。
比如下图中左边的图形是凸集,而右边不是,因为我们可以找到两个点,使它们之间的线段上的点不在集合中
数学上,凸集的定义如下:
给定集合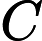




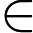
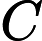

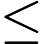

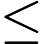










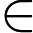
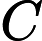
我们就称集合C是凸集,我们把点








1.2 什么是凸函数?
假设有一个函数
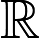

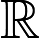
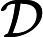



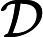


















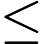















那么就称
注意:定义域是凸集这个要求不是必须的,其出发点只是为了使x,y的凸组合有定义
关于凸函数,直观上可以用下图来加深理解:
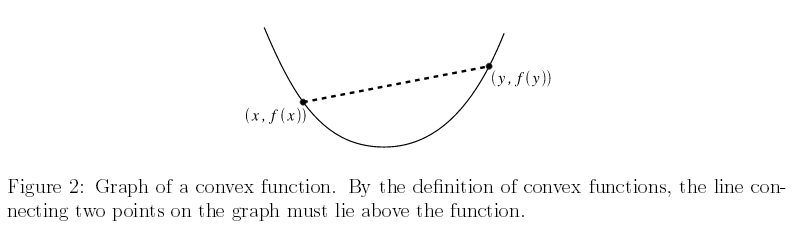
简单来说,我们在定义域任取两个点x,y, 连接他们得到一条线段,如果这个线段上的点都位于对应函数值上方,我们就说该函数是一个凸函数。
更进一步,如果
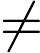













1.3 凸函数的等价判别方法
上面我们讲了什么是凸函数,然而这个定义在现实中很难用于判断一个函数是不是凸的,因此介绍几个等价的定义。
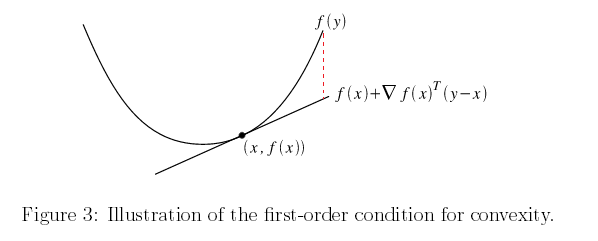
1.3.1 一阶近似
假设函数
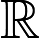

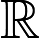














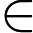
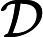







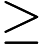
















我们将



















1.3.2 二阶近似
假设函数
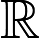

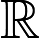







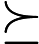

可能有些同学忘了海塞矩阵长什么样了,这里提一下。假设我们的变量来自n维空间,即
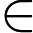
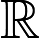


















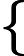


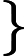






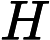

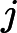

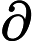





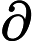


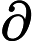

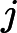
也就是说,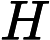

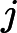



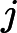
1.4 凸优化问题
上面已经介绍了凸集和凸函数,是时候到凸优化了吧? 别急,在介绍凸优化概念之前再啰嗦两句。
1.4.1 水平子集(sublevel sets)
由凸函数的概念出发,我们可以引出水平子集(sublevel set)的概念。假定f(x)是一个凸函数, 给定一个实数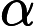
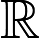
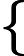

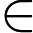
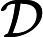



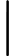




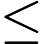
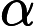
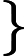
叫做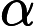

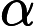
















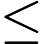















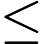

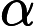






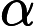

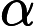
水平子集告诉我们,给凸函数添加一个上限,定义域内剩下的点构成的点集还是一个凸集。
1.4.2 仿射函数(affine functions)
数学上,我们把形如
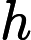




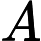



的函数叫做仿射函数。其中,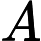

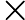
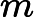

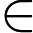
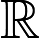
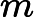
同理,我们可以证明,点集
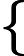

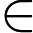
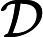

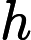

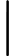
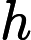





是一个凸集,证明略。
1.4.3 凸优化(convex optimization)
那么回到凸优化问题上来, 什么是一个凸优化问题?
一个凸优化问题可以定义为:
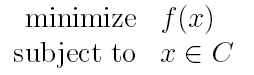
其中f是一个凸函数,C是一个凸集。根据先前介绍过的水平子集等概念,上面问题又可以等价写为:
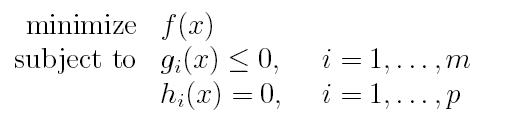
其中,g(x)是凸函数,h(x)是仿射函数。 也就是说,原约束集C被我们表示为一系列凸集的交集(数学上可以证明,凸集的交集还是凸集)。
1.4.4 局部最优(local optima)和全局最优(global optima)
局部最优:周围小范围 内没有比我小的点。
数学定义:
如果存在




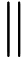







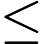


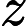

全局最优:我就是整个定义域中的最小的点。
数学定义:
如果对于定义域内的所有z,有



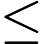


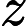

现在回到凸优化问题上, 对于凸优化问题,有一个很重要的结论:
对于凸函数来讲, 局部最优就是全局最优。证明如下:
我们用反证法证明。设
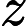







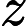
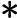

由x的局部最优性质,我们有 :
存在


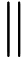


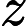
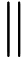







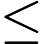


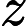

我们考虑
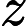
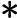
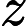









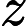
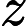
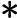

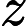





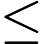


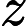

另一方面,由凸函数性质,我们有:


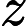












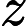
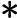

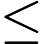













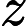
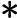






















由此得

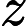










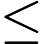


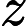


1.5 常见凸优化问题
- 线性规划
如果
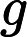


- 二次规划
线性规划中,如果
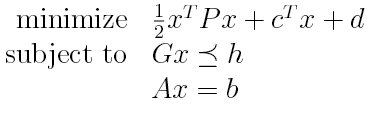
- 二次约束二次规划

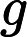


- 半定规划
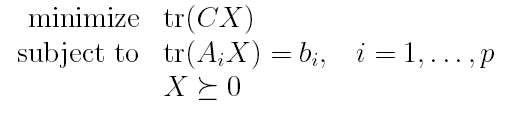
其中,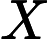
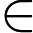
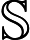

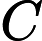

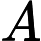

- 凸优化中的基本概念
- 凸优化中的基本概念
- 凸优化的基本概念
- 网站优化基本概念
- oracle数据库优化--基本概念
- sql优化基本概念
- oracle数据库优化--基本概念
- 组合优化基本概念
- 数据库基本概念及优化
- MySQL性能优化基本概念
- 凸优化学习笔记(三)之凸集基本概念
- MPEG2中的一些基本概念
- Lucene中的基本概念
- Lucene中的基本概念
- CMM中的基本概念
- ExtJS中的基本概念
- 视频中的基本概念
- CPP 中的一些基本概念
- 侯世达:为什么人工智能还远远谈不上「智能」?
- 06-Spring-Spring中的事务操作
- 图形用户界面
- 07-Spring-spring中使用jdbc
- 阿里巴巴发布 AliGenie 语音开放平台「智联网」战略又落一子
- 凸优化中的基本概念
- 单调队列的简单运用
- C 和 C++ 中的mian函数解析
- 08-Spring-spring整合hibernate
- 美国加州放宽路测条件,自动驾驶汽车可于明年进行「无人」测试
- 删除创建时间超过七天的文件
- 2017.10.24 LeetCode 88. Merge Sorted Array 【思维呀】
- 51nod 1618 树或非树 树链剖分+线段树
- angularjs过滤、全选、删除


