LDA主题模型要概括

本博客原文
本文为学习LDA主题模型的笔记，主要是对LDA主题模型进行一个简单的概括，具体的细节及推导可以参见:

非常详细的参考资料

一、问题提出

什么是主题模型？什么是LDA?

将文档集中，每篇文档的主题按照概率分布的形式给出，属于无监督的学习算法。需要的输入仅仅是文档集和指定的文档主题数量K

隐含狄利克雷分布(Latent Dirichlet allocation)简称LDA。LDA是一种典型的词袋模型，词与词之间没有顺序及先后关系。一篇文档可以包含多个主题，文档中的每个词都由其中一个主题生成。

二、必备知识

• 蒙特卡洛方法、马尔科夫链、MCMC采样和M-H采样，Gibbs采样 。参考资料
• EM算法。参考资料:统计学习方法EM算法
• 概率论相关知识以及一些优化算法(如牛顿法等)

三、概述

LDA维基百科

LDA模型中，一篇文档的生成方式如下

• 从狄利克雷分布中取样生成文档i的主题分布θi
• 从主题的多项式分布θi 中取样生成文档i第j个词的主题zi,j
• 从狄利克雷分布β 中取样生成主题Zi,j的词语分布Φzi,j
• 从词语的多项式分布Φzi,j中采样最终生成词语ωi,j

即：主题分布–> 主题–>词语分布–>词语

共轭先验分布

在贝叶斯统计中，如果后验分布与先验分布属于同类，则先验分布与后验分布被称为共轭分布，而先验分布被称为似然函数的共轭先验

Beta分布是二项分布的共轭先验分布，Dirichlet分布是多项分布的共轭先验分布

LDA主题模型

目标:找到每一篇文档中的主题分布和每一个主题中词的分布

LDA的模型图如下(图片来自pinard博客)

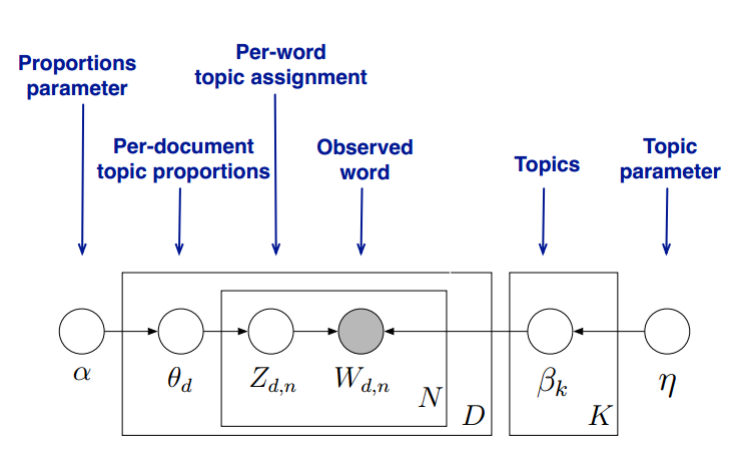
LDA假设主题中词的先验分布是Dirichlet分布，即对任一文档d，其主题分布θd为

θd=Dirichlet(α⃗ ) ,α⃗ 是K维(主题数)向量

LDA假设主题中词的先验分布是Dirichlet分布，即对任一主题k，其词分布为

βk=Dirichlet(η⃗ ) , η⃗  是V维(词汇表中词数)向量

对任一文档d中第n个词，可以从主题分布θd 中获得它的主题编号zdn 的分布为

zdn=multi(θd)

而对于该主题，得到我们看到的词Wdn的概率为

Wdn=multi(βzdn)

设在文档d中，第k个主题的次数为n(k)d ,则对应多项分布的计数为nd→=(n(1)d,n(2)d,...,n(k)d)

根据Dirichlet-Multi共轭，有θd的后验分布为

Dirichlet(θd|nd→+α⃗ ) (新的文档-主体分布)

同理，设第k个主题中，第v个词的个数为n(v)k ,则对应的多项分布的计数为nk→=(n(1)k,n(2)k,...,n(V)k)

根据Dirichlet-Multi共轭，有βk 的后验分布为

Dirichlet(βk|nk→+η⃗ )

主题产生词不依赖具体文档，这说明文档-主题分布和主题-词分布是独立的。

以上是LDA基本原理，剩下需要解决的问题是

基于一个LDA模型，如何求解每一篇文档的主题分布和每个主题的词分布，即如何求解 θd 和βk

求解LDA的方法有Gibbs采样和变分推断EM两种

四、Gibbs采样求解LDA

Gibbs采样解决的是使采样数据符合指定分布的问题。在了解Gibbs采样之前，先了解一下蒙特卡洛方法。

蒙特卡洛方法

蒙特卡洛方法是一种随机的方法。我们在中小学时学习过使用投针实验估计圆周率的问题就是属于蒙特卡洛方法。一般地，蒙特卡洛方法可用来解决定积分(投针实验可以看作是求解0~r上圆形曲线的定积分问题)。

对于∫baf(x)dx ,若f(x)的原函数较难求解，则可以使用蒙特卡洛方法近似

在[a,b]上随机采样n个点，x1,x2,...,xn

∫baf(x)dx≈b−an∑ni=1f(xi)

如果数学过关，那么很容易可以发现上述方法必须基于x在[a,b]上是均匀分布。然而多数情况下x并不均匀。若x在[a,b]上的概率分布函数为p(x),那么

∫baf(x)dx=∫baf(x)p(x)⋅p(x)≈1n∑ni=1f(xi)p(xi)

以上我们知道了如何求任意概率分布下的f(x)的定积分，但是还有一个非常重要的问题没有解决，即如何使采样数据符合我们指定的概率分布，这也是我们需要研究的重点。

对于均匀分布，采样十分简单，一般通过线性同余发生器就可以产生0~1之间的伪随机数，并且很多常见的分布都可以根据均匀分布转化。

对于无法转化的分布，可采用接受-拒绝采样的方法。

马尔科夫链

马尔科夫链介绍

使用接受-拒绝 采样的时间复杂度通常很高，如果需要对大量的数据进行采样，不太适用。因此引入马尔科夫链。

马尔科夫链的每一个时刻状态转移只依赖于上一个状态。

上图构成的马尔科夫链，定义p(i,j)为p(j|i), 定义牛市状态为0，熊市状态为1,很盘状态为2,这样得到的马尔科夫链模型的状态转移矩阵为

p=⎛⎝⎜0.90.150.250.0750.80.250.0250.050.5⎞⎠⎟

马尔科夫链性质

马尔科夫链具有一个非常好的性质，就是对应不同的初始状态，按照马尔科夫链进行转移，最终会收敛到同一状态，也就是说收敛到的稳定概率分布与初始状态概率分布无关。

这个性质为什么好呢？因为一旦我们知道了某个概率分布对应的状态转移矩阵，则可以用任意的概率分布样本开始，代入马尔科夫链的状态转移矩阵，最终得到符合对应概率分布的样本。

该性质对于大部分的马尔科夫链都成立，并且连续状态时也成立。

基于马尔科夫链的采样

如果可以得到某个分布对应的马尔科夫链状态转移矩阵，就可以采样出符合该分布的样本集。

首先根据高斯分布或其他分布π0(x) 采样得到初始状态x0 基于条件概率分布p(x0|x) 采样得到x1，如此进行下去，直到马尔科夫状态转移矩阵收敛。n次后，马尔科夫链收敛到平稳分布π(x) 再开始采样

接下来就是如何根据指定分布得到状态转移矩阵了。

MCMC采样和M-H采样

具体的推导过程可以参考pinard的博客 ， 这里不再推导证明，只简述采样过程。

马尔科夫链的细致平稳条件为

πP=π

也就满足马尔科夫链的收敛性，也就是说，只要找使概率分布π(x)满足细致平稳分布的矩阵。

MCMC采样

一般情况下

π(i)Q(i,j)≠π(j)Q(j,i)

引入一个α(i,j) ，使

π(i)Q(i,j)α(i,j)=π(j)Q(j,i)α(j,i)

只要令

α(i,j)=π(j)Q(j,i)

α(j,i)=π(i)Q(i,j)

一般称α(i,j) 为接受率。取值在[0,1]之间。这也就是说，目标矩阵P可以通过任意一个马尔科夫链转移矩阵以一定的接受率获得。

MCMC采样过程

摘自Pinard博客

• 输入任意选定的马尔科夫链状态转移矩阵Q,平稳分布π(x) ,设定状态转移次数阈值n1,需要的样本次数n2

• 从任意简单的概率分布采样得到初始状态X0

• 从 t=0~n1+n2-1

  ​ a) 从条件概率分布Q(x|xt) 中采样得到样本X∗

  ​ b) 从均匀分布[0,1]中采样得到u

  ​ c) 如果u<α(xt,x∗)=π(x∗)Q(x∗,xt) 则接受转移xt→x∗ ，即xt+1=x∗

  ​ d) 否则不接受,t=max(t-1,0)

得到样本集(xn1,xn1+1,...,xn1+n2−1)

MCMC存在的问题

当接受率较小时，采样所需时间开销很大。

M-H采样

由于MCMC采样存在的问题，因此提出M-H采样

马尔科夫链的细致平稳条件

π(i)Q(i,j)α(i,j)=π(j)Q(j,i)α(j,i)

此时如果把两边同时扩大，细致平稳条件依然满足，因此，假设原来的α(i,j)=0.1 α(j,i)=0.2 则两边都乘5，以增大接受率

M-H采样过程和MCMC采样类似，唯一的区别是第三步的c

c) 如果α(xt,x∗)=min(π(j)Q(j,i)π(i)Q(i,j)),1)>u ,则接受

Gibbs 采样

M-H存在的缺陷主要有两点，一是由于接受率的问题导致算法收敛时间变长；二是对于有些高维数据，联合分布概率不好求，而条件概率好求时，M-H不适用。

Gibbs采样克服了以上两点问题。

同样的，这里不详细推导，只说明Gibbs采样的流程。

观察马尔科夫平稳细致条件可以发现，对于二维数据，在x1=x(1)1 这条直线上，如果使用条件概率分布π(x2|x(1)1) 作为马尔科夫链的状态转移概率，则任意两个点满足细致平稳条件。

结论：平面上任意两点E,F，满足细致平稳条件

π(E)P(E→F)=π(F)P(F→E)

二维Gibbs采样

过程

• 输入平稳分布π(x1,x2) , 设定状态转移次数阈值n1,需要的样本个数n2

• 随机初始化初始状态值x(1)1 和 x(1)2

• 从 t=0 ~ n1+n2-1

  ​ a) 从条件概率分布P(x2|x(t)1) 中采样得到样本x(t+1)2

  ​ b) 从条件概率分布P(x1|x(t+1)2) 中采样得到样本x(t+1)1

多维Gibbs采样类比

Gibbs 采样方法解LDA

求解LDA即根据已知所有文档形成的词向量ω⃗  , 先求出词ω 和主题z 的联合分布P(ω⃗ ,z⃗ )，进而求出某一个词对应主题的条件概率分布P(zi=k|ω⃗ ,zΓi→) ,zΓi→ ,表示去掉下标为i的词后的主题分布。有了这个条件概率分布，就可以进行Gibbs采样，在采样收敛后得到第i个词的主题。

得到每个词的主题后，通过统计每个主题的词数，得到各个主题的词分布。通过统计各个文档对应词的主题分布，得到文档主题分布。

得到联合分布

p(w⃗ ,z⃗ )∝p(w⃗ ,z⃗ |α⃗ ,η⃗ )=p(z⃗ |α⃗ )p(w⃗ |z⃗ ,η⃗ )=∏Md=1△(n⃗ d+α⃗ )△(α⃗ )∏Kk=1△(n⃗ k+η⃗ )△(η⃗ )

得到条件概率

p(zi=k|w⃗ ,z⃗ ¬i)∝p(zi=k,wi=t|w⃗ ¬i,z⃗ ¬i)=∫p(zi=k,wi=t,θ⃗ d,β⃗ k|w⃗ ¬i,z⃗ ¬i)dθ⃗ ddβ⃗ k=∫p(zi=k,θ⃗ d|w⃗ ¬i,z⃗ ¬i)p(wi=t,β⃗ k|w⃗ ¬i,z⃗ ¬i)dθ⃗ ddβ⃗ k=∫p(zi=k|θ⃗ d)p(θ⃗ d|w⃗ ¬i,z⃗ ¬i)p(wi=t|β⃗ k)p(β⃗ k|w⃗ ¬i,z⃗ ¬i)dθ⃗ ddβ⃗ k=∫p(zi=k|θ⃗ d)Dirichlet(θ⃗ d|n⃗ d,¬i+α⃗ )dθ⃗ d∗∫p(wi=t|β⃗ k)Dirichlet(β⃗ k|n⃗ k,¬i+η⃗ )dβ⃗ k=∫θdkDirichlet(θ⃗ d|n⃗ d,¬i+α⃗ )dθ⃗ d∫βktDirichlet(β⃗ k|n⃗ k,¬i+η⃗ )dβ⃗ k=EDirichlet(θd)(θdk)EDirichlet(βk)(βkt)

EDirichlet(θd)(θdk)=nkd,¬i+αk∑s=1Knsd,¬i+αs

EDirichlet(βk)(βkt)=ntk,¬i+ηt∑f=1Vnfk,¬i+ηf

因此

p(zi=k|w⃗ ,z⃗ ¬i)=nkd,¬i+αk∑s=1Knsd,¬i+αsntk,¬i+ηt∑f=1Vnfk,¬i+ηf

有了条件概率公式，就能进行Gibbs采样，当Gibbs采样收敛时，就能得到所有词的采样主题。

LDA Gibbs采样算法流程

训练流程

1) 选择合适的主题数K ,选择合适的超参数向量α⃗ ,η⃗ 

2) 对应语料库中每个篇文档的每一个词，随机赋予一个主题编号z

3) 重新扫描语料库，对于每一个词，利用Gibbs采样公式，更新它的topic编号，并更新语料库中该词的编号

4) 重复3直至Gibbs采样收敛

5) 统计语料库中各个文档各个词的主题，得到文档主题分布θd ,统计语料库中各个主题的词的分布，得到LDA的主 题与词的分布βk

预测流程

当新文档出现时，如何统计得到该文档的主题？此时LDA的主题-词分布的参数βk 已经确定，需要得到的是文档的主题分布。

换句话说，就是在Gibbs采样时，EDirichlet(βk)(βkt) 已知，只需对前半部分 EDirichlet(θd)(θdk) 进行采样计算即可

1) 对当前文档主题的每个词，随机赋予一个主题编号z

2) 重新扫描当前文档，对每一个词，利用Gibbs采样公式，更新它的topic编号

3) 重复2直至Gibbs采样收敛

4) 统计文档中各个词的主题，得到该文档的主题分布

五、变分推断EM求解LDA

EM算法

EM算法解决的问题是求解含有隐变量的概率模型的参数极大似然估计或极大后验概率估计

• 输入:观测变量数据Y，隐变量数据Z，完全数据的联合分布P(Y,Z|θ)，隐变量的条件分布P(Z\vertY,θ)
• 输出:模型参数

EM算法一般分为E步和M步两步，E步是求完全数据对于隐变量的期望，M步为最大化这个期望，至于为什么是求期望，是根据极大似然估计推导得出。

变分推断EM算法求解LDA

参考资料

变分推断EM通过变分推断和EM来得到LDA的文档主题分布和主题词分布

LDA模型中的隐藏变量为θ,β,z ，模型的参数为α,η 。求解它的主要思想是，使用EM算法在E步求出隐藏变量θ,β,z 的基于条件概率分布的期望，然后再M步极大化这个期望，然后得到更新后的参数α,η 。

然而现在的问题是，我们难以求出θ,β,z 的条件概率分布。因此需要“变分推断”方法，通过变分假设，假设所有的隐藏变量都是通过各自的独立分布形成。即

接下来就是如何求γ,Φ,λ 以及解LDA了，具体推导参见该链接