225. Implement Stack using Queues

Implement the following operations of a stack using queues.

• push(x) -- Push element x onto stack.
• pop() -- Removes the element on top of the stack.
• top() -- Get the top element.
• empty() -- Return whether the stack is empty.

Notes:

• You must use only standard operations of a queue -- which means onlypush to back, peek/pop from front, size, andis empty operations are valid.
• Depending on your language, queue may not be supported natively. You may simulate a queue by using a list or deque (double-ended queue), as long as you use only standard operations of a queue.
• You may assume that all operations are valid (for example, no pop or top operations will be called on an empty stack).

官方解答：

Summary

This article is for beginners. It introduces the following ideas:Stack, Queue.

Solution

---

Approach #1 (Two Queues, push - $O(1)$, pop $O(n)$ )

Intuition

Stack is LIFO (last in - first out) data structure, in which elements are added and removed from the same end, calledtop.In general stack is implemented using array or linked list, but in the current article we will review a different approach for implementing stack using queues. In contrast queue isFIFO (first in - first out) data structure, in which elements are added only from the one side -rear and removed from the other - front. In order to implement stack using queues, we need to maintain two queuesq1 and q2. Also we will keep top stack element in a constant memory.

Algorithm

Push

The new element is always added to the rear of queue q1 and it is kept astop stack element

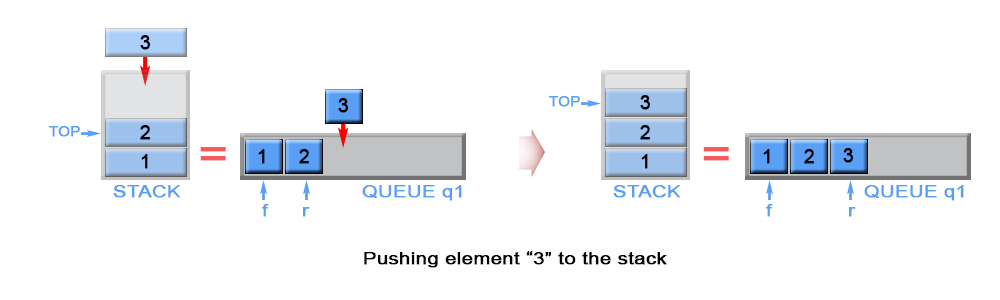
Figure 1. Push an element in stack

Java

private Queue<Integer> q1 = new LinkedList<>();private Queue<Integer> q2 = new LinkedList<>();private int top;// Push element x onto stack.public void push(int x) {    q1.add(x);    top = x;}

Complexity Analysis

• Time complexity : $O(1)$. Queue is implemented as linked list and add operation has $O(1)$ time complexity.

• Space complexity : $O(1)$

Pop

We need to remove the element from the top of the stack. This is the last inserted element inq1.Because queue is FIFO (first in - first out) data structure, the last inserted element could be removed only after all elements, except it, have been removed. For this reason we need to maintain additional queueq2, which will serve as a temporary storage to enqueue the removed elements from q1. The last inserted element inq2 is kept as top. Then the algorithm removes the last element in q1. We swap q1 with q2 to avoid copying all elements fromq2 to q1.

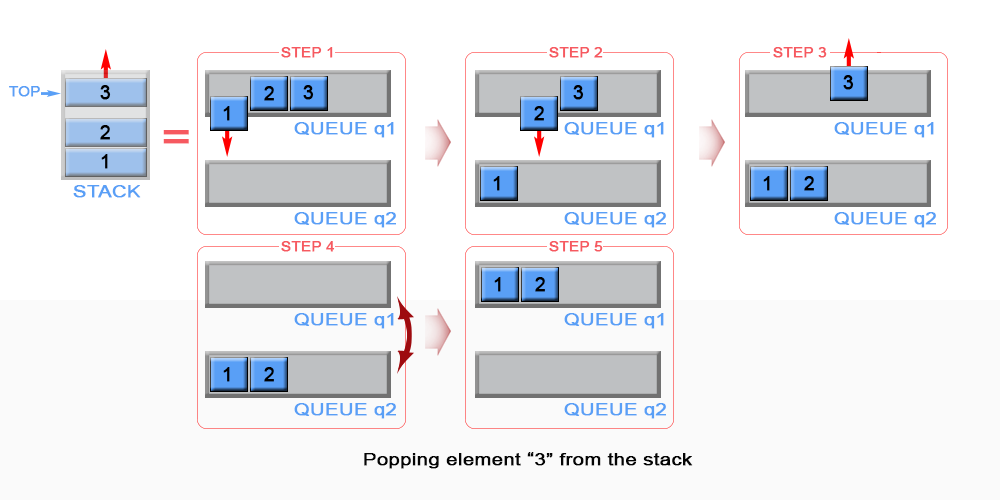
Figure 2. Pop an element from stack

Java

// Removes the element on top of the stack.public void pop() {    while (q1.size() > 1) {        top = q1.remove();        q2.add(top);    }    q1.remove();    Queue<Integer> temp = q1;    q1 = q2;    q2 = temp;}

Complexity Analysis

• Time complexity : $O(n)$. The algorithm dequeues n elements from q1 and enqueues $n-1$ elements to q2, where $n$ is the stack size. This gives $2n-1$ operations.
• Space complexity : $O(1)$.

---

Approach #2 (Two Queues, push - $O(n)$, pop $O(1)$ )

Algorithm

Push

The algorithm inserts each new element to queue q2 and keep it as thetop element. In case queue q1 is not empty (there are elements in the stack), we remove all elements fromq1 and add them to q2. In this way the new inserted element (top element in the stack) will be always positioned at the front ofq2. We swap q1 with q2 to avoid copying all elements fromq2 to q1.

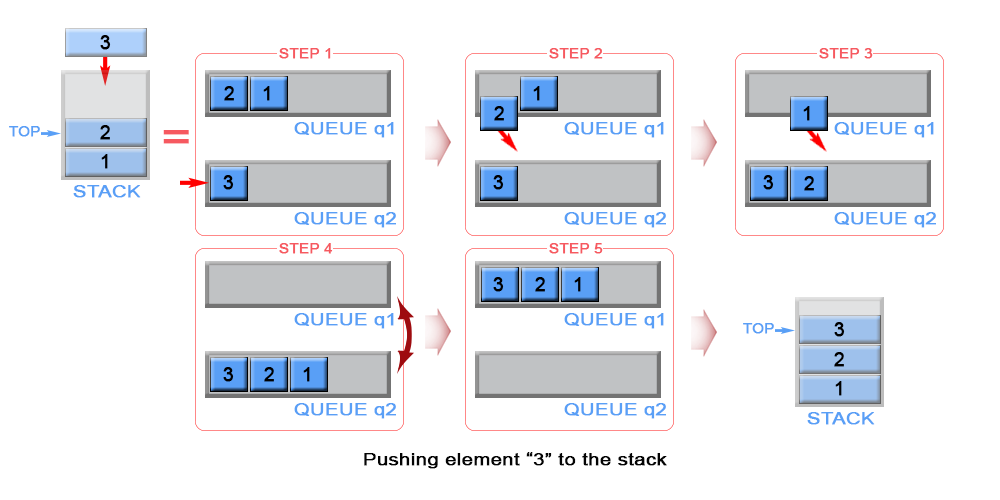
Figure 3. Push an element in stack

Java

public void push(int x) {    q2.add(x);    top = x;    while (!q1.isEmpty()) {                        q2.add(q1.remove());    }    Queue<Integer> temp = q1;    q1 = q2;    q2 = temp;}

Complexity Analysis

• Time complexity : $O(n)$. The algorithm removes n elements from q1 and inserts $n+1$ elements to q2, where n is the stack size. This gives $2n+1$ operations. The operations add and remove in linked lists has$O(1)$ complexity.

• Space complexity : $O(1)$.

Pop

The algorithm dequeues an element from queue q1 and keeps front element ofq1 as top.

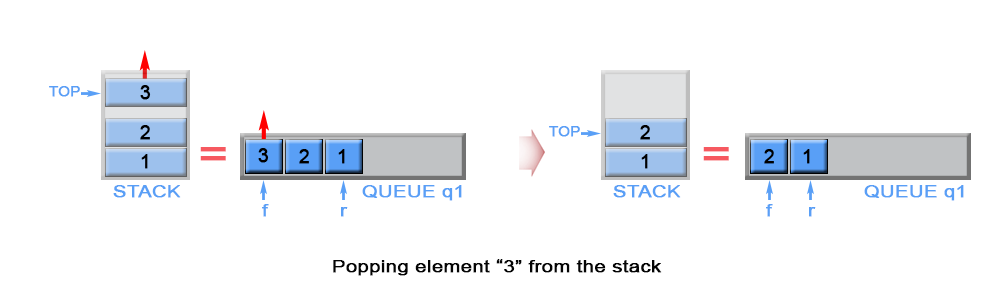
Figure 4. Pop an element from stack

Java

// Removes the element on top of the stack.public void pop() {    q1.remove();    if (!q1.isEmpty()) {        top = q1.peek();    }}

Complexity Analysis

• Time complexity : $O(1)$.
• Space complexity : $O(1)$.

In both approaches empty and top operations have the same implementation.

Empty

Queue q1 always contains all stack elements, so the algorithm checksq1 size to return if the stack is empty.

// Return whether the stack is empty.public boolean empty() {    return q1.isEmpty();}

Time complexity : $O(1)$.

Space complexity : $O(1)$.

Top

The top element is kept in constant memory and is modified each time when we push or pop an element.

// Get the top element.public int top() {    return top;}

Time complexity : $O(1)$. The top element has been calculated in advance and only returned intop operation.

Space complexity : $O(1)$.

---

Approach #3 (One Queue, push - $O(n)$, pop $O(1)$ )

The mentioned above two approaches have one weakness, they use two queues. This could be optimized as we use only one queue, instead of two.

Algorithm

Push

When we push an element into a queue, it will be stored at back of the queue due to queue's properties.But we need to implement a stack, where last inserted element should be in the front of the queue, not at the back. To achieve this we can invert the order of queue elements when pushing a new element.

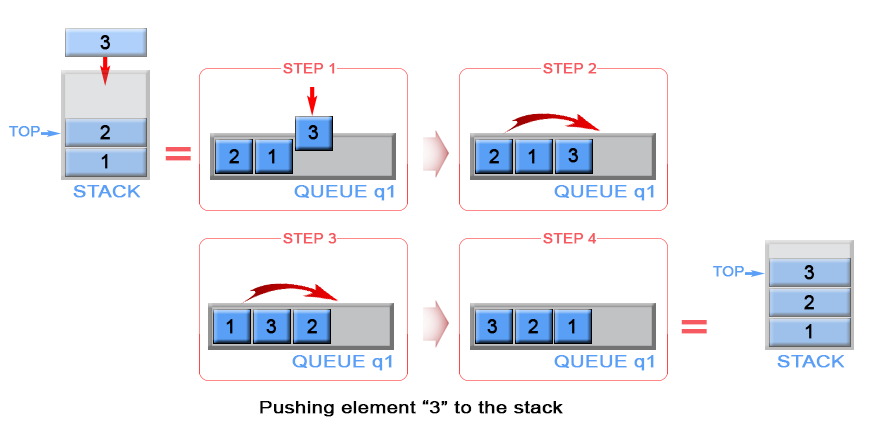
Figure 5. Push an element in stack

Java

private LinkedList<Integer> q1 = new LinkedList<>();// Push element x onto stack.public void push(int x) {    q1.add(x);    int sz = q1.size();    while (sz > 1) {        q1.add(q1.remove());        sz--;    }}

Complexity Analysis

• Time complexity : $O(n)$. The algorithm removes n elements and inserts $n+1$ elements to q1 , where n is the stack size. This gives $2n+1$ operations. The operations add and remove in linked lists has$O(1)$ complexity.

• Space complexity : $O(1)$.

Pop

The last inserted element is always stored at the front of q1 and we can pop it for constant time.

Java

// Removes the element on top of the stack.public void pop() {    q1.remove();}

Complexity Analysis

• Time complexity : $O(1)$.
• Space complexity : $O(1)$.

Empty

Queue q1 contains all stack elements, so the algorithm checks if q1 is empty.

// Return whether the stack is empty.public boolean empty() {    return q1.isEmpty();}

Time complexity : $O(1)$.

Space complexity : $O(1)$.

Top

The top element is always positioned at the front of q1. Algorithm return it.

// Get the top element.public int top() {    return q1.peek();}

Time complexity : $O(1)$.

Space complexity : $O(1)$.

Analysis written by: @elmirap.

类似的题目有：

232. Implement Queue using Stacks

Implement the following operations of a queue using stacks.

• push(x) -- Push element x to the back of queue.
• pop() -- Removes the element from in front of queue.
• peek() -- Get the front element.
• empty() -- Return whether the queue is empty.

Notes:

• You must use only standard operations of a stack -- which means onlypush to top, peek/pop from top, size, and is empty operations are valid.
• Depending on your language, stack may not be supported natively. You may simulate a stack by using a list or deque (double-ended queue), as long as you use only standard operations of a stack.
• You may assume that all operations are valid (for example, no pop or peek operations will be called on an empty queue).

官方解答：

Summary

This article is for beginners. It introduces the following ideas:Queue, Stack.

Solution

Queue is FIFO (first in - first out) data structure, in which the elements are inserted from one side -rear and removed from the other - front.The most intuitive way to implement it is with linked lists, but this article will introduce another approach using stacks.Stack isLIFO (last in - first out) data structure, in which elements are added and removed from the same end, calledtop.To satisfy FIFO property of a queue we need to keep two stacks. They serve to reverse arrival order of the elements and one of them store the queue elements in their final order.

---

Approach #1 (Two Stacks) Push -$O(n)$ per operation, Pop - $O(1)$ per operation.

Algorithm

Push

A queue is FIFO (first-in-first-out) but a stack is LIFO (last-in-first-out). This means the newest element must be pushed to the bottom of the stack. To do so we first transfer alls1 elements to auxiliary stack s2. Then the newly arrived element is pushed on top ofs2 and all its elements are popped and pushed to s1.

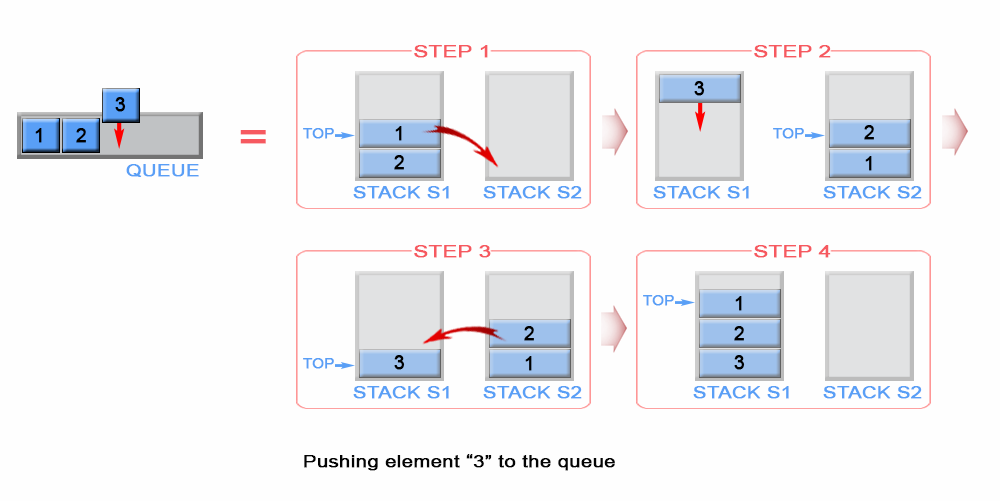
Figure 1. Push an element in queue

Java

private int front;public void push(int x) {    if (s1.empty())        front = x;    while (!s1.isEmpty())        s2.push(s1.pop());    s2.push(x);    while (!s2.isEmpty())        s1.push(s2.pop());}

Complexity Analysis

• Time complexity : $O(n)$.

Each element, with the exception of the newly arrived, is pushed and popped twice. The last inserted element is popped and pushed once. Therefore this gives$4n+2$ operations where $n$ is the queue size. The push and pop operations have $O(1)$ time complexity.

• Space complexity : $O(n)$.We need additional memory to store the queue elements

Pop

The algorithm pops an element from the stack s1, because s1 stores always on its top the first inserted element in the queue.The front element of the queue is kept asfront.

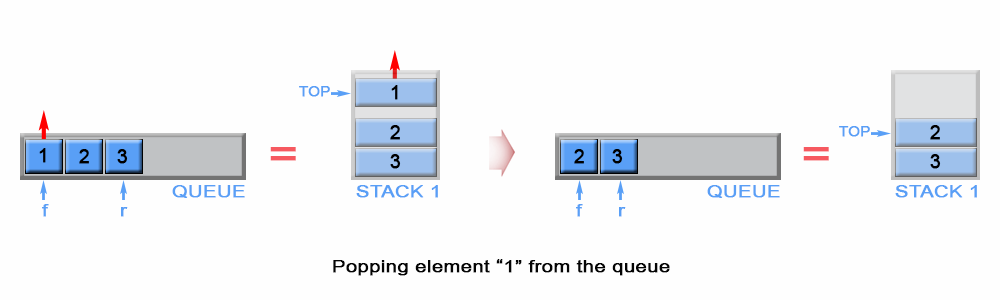
Figure 2. Pop an element from queue

Java

// Removes the element from the front of queue.public void pop() {    s1.pop();    if (!s1.empty())        front = s1.peek();}

Complexity Analysis

• Time complexity : $O(1)$.
• Space complexity : $O(1)$.

Empty

Stack s1 contains all stack elements, so the algorithm checks s1 size to return if the queue is empty.

// Return whether the queue is empty.public boolean empty() {    return s1.isEmpty();}

Time complexity : $O(1)$.

Space complexity : $O(1)$.

Peek

The front element is kept in constant memory and is modified when we push or pop an element.

// Get the front element.public int peek() {  return front;}

Time complexity : $O(1)$.Thefront element has been calculated in advance and only returned in peek operation.

Space complexity : $O(1)$.

---

Approach #2 (Two Stacks) Push - $O(1)$ per operation, Pop - Amortized $O(1)$ per operation.

Algorithm

Push

The newly arrived element is always added on top of stack s1 and the first element is kept asfront queue element

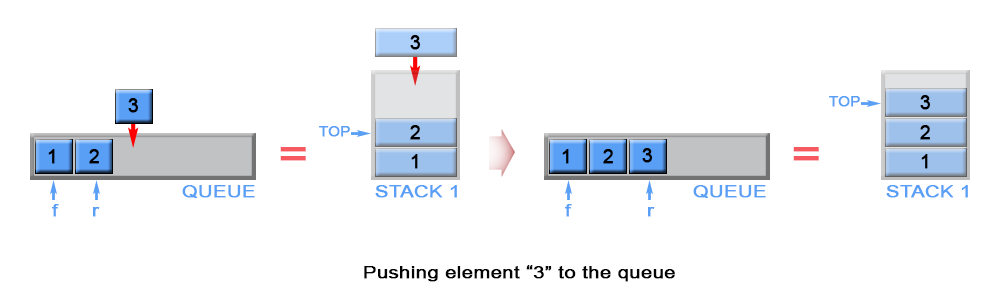
Figure 3. Push an element in queue

Java

private Stack<Integer> s1 = new Stack<>();private Stack<Integer> s2 = new Stack<>();// Push element x to the back of queue.public void push(int x) {    if (s1.empty())        front = x;    s1.push(x);}

Complexity Analysis

• Time complexity : $O(1)$.

Аppending an element to a stack is an O(1) operation.

• Space complexity : $O(n)$.We need additional memory to store the queue elements

Pop

We have to remove element in front of the queue. This is the first inserted element in the stacks1 and it is positioned at the bottom of the stack because of stack'sLIFO (last in - first out) policy. To remove the bottom element froms1, we have to pop all elements from s1 and to push them on to an additional stacks2, which helps us to store the elements of s1 in reversed order. This way the bottom element ofs1 will be positioned on top of s2 and we can simply pop it from stacks2. Once s2 is empty, the algorithm transfer data from s1 to s2 again.

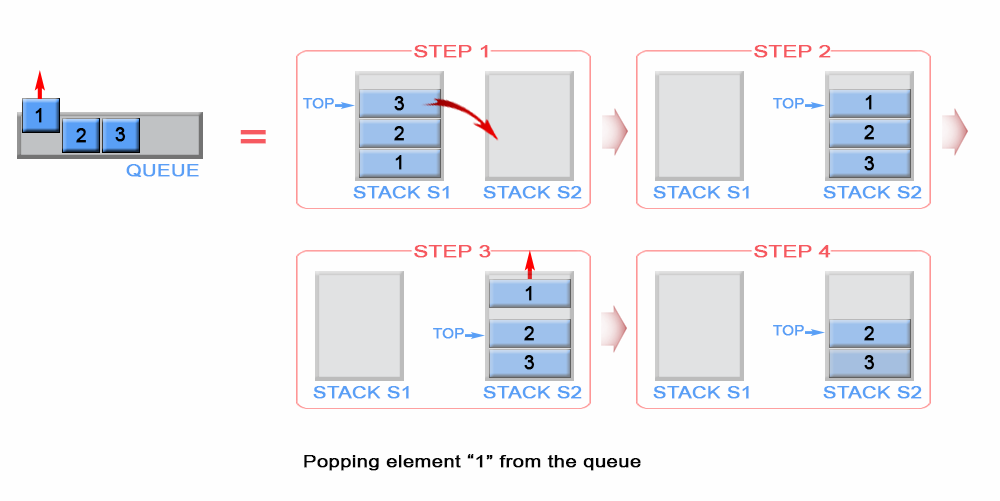
Figure 4. Pop an element from stack

Java

// Removes the element from in front of queue.public void pop() {    if (s2.isEmpty()) {        while (!s1.isEmpty())            s2.push(s1.pop());    }    s2.pop();    }

Complexity Analysis

• Time complexity: Amortized $O(1)$, Worst-case $O(n)$.

In the worst case scenario when stack s2 is empty, the algorithm pops$n$ elements from stack s1 and pushes $n$ elements to s2, where $n$ is the queue size. This gives $2n$ operations, which is $O(n)$. But when stack s2 is not empty the algorithm has $O(1)$ time complexity. So what does it mean by Amortized $O(1)$? Please see the next section on Amortized Analysis for more information.

• Space complexity : $O(1)$.

Amortized Analysis

Amortized analysis gives the average performance (over time) of each operation in the worst case. The basic idea is that a worst case operation can alter the state in such a way that the worst case cannot occur again for a long time, thus amortizing its cost.

Consider this example where we start with an empty queue with the following sequence of operations applied:

push1,push2,…,pushn,pop1,pop2…,popnpush_1, push_2, \ldots, push_n, pop_1,pop_2 \ldots, pop_npush​1​​,push​2​​,…,push​n​​,pop​1​​,pop​2​​…,pop​n​​

The worst case time complexity of a single pop operation is $O(n)$. Since we have $n$ pop operations, using the worst-case per operation analysis gives us a total of O(n2)O(n^2)O(n​2​​) time.

However, in a sequence of operations the worst case does not occur often in each operation - some operations may be cheap, some may be expensive. Therefore, a traditional worst-case per operation analysis can give overly pessimistic bound. For example, in a dynamic array only some inserts take a linear time, though others - a constant time.

In the example above, the number of times pop operation can be called is limited by the number of push operations before it. Although a single pop operation could be expensive, it is expensive only once pern times (queue size), when s2 is empty and there is a need for data transfer betweens1 and s2. Hence the total time complexity of the sequence is :n (for push operations) + 2*n (for first pop operation) +n - 1 ( for pop operations) which is $O(2\ast n)$.This gives $O(2n/2n)$ = $O(1)$ average time per operation.

Empty

Both stacks s1 and s2 contain all stack elements, so the algorithm checkss1 and s2 size to return if the queue is empty.

// Return whether the queue is empty.public boolean empty() {    return s1.isEmpty() && s2.isEmpty();}

Time complexity : $O(1)$.

Space complexity : $O(1)$.

Peek

The front element is kept in constant memory and is modified when we push an element. Whens2 is not empty, front element is positioned on the top of s2

// Get the front element.public int peek() {    if (!s2.isEmpty()) {            return s2.peek();    }    return front;}

Time complexity : $O(1)$.

The front element was either previously calculated or returned as a top element of stacks2. Therefore complexity is $O(1)$

Space complexity : $O(1)$.