支持向量机（一）

超平面：分类的决策边界
间隔：点到分割面的距离
支持向量：就是离分隔超平面最近的那些点。

我们这里将g(z)做一个简化，将其简单映射到y=-1和y=1上。映射关系如下：

例子：可以拿一根线来将两种不同颜色的点分开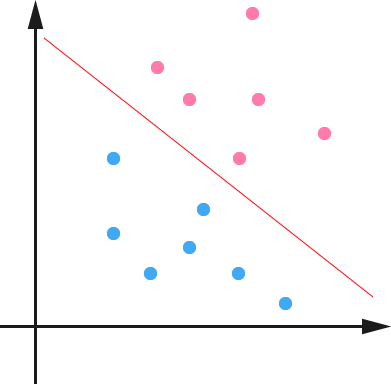

这条红颜色的线就是超平面，超平面把这两种不同颜色的数据点分隔开来，在超平面一边的数据点所对应的 y 全是 -1 ，而在另一边全是 1 。

设分类函数：
显然，如果 f(x)=0，那么x 是位于超平面上的点。我们不妨设对于所有满足f(x)<0 的点，其对应的 y 等于-1，而 f(x)>0 则对应 y=1 的数据点。

我们在进行分类的时候，将数据点 x代入f(x) 中，如果得到的结果小于 0，则赋予其类别 -1，如果大于 0 则赋予类别 1 。如果 f(x)=0，则很难办了，分到哪一类都不是。

如何确定w和b
一般而言，一个点距离超平面的远近可以表示为分类预测准确程度。
在超平面w*x+b=0确定的情况下，|w*x+b|能够相对的表示点x到距离超平面的远近，而w*x+b的符号与类标记y的符号是否一致表示分类是否正确，所以，可以用量y*(w*x+b)的正负性来判定或表示分类的正确性和确信度。即为label*(w*x+b)。

定义函数间隔（functional margin）：
定义超平面(w，b)关于训练数据集T的函数间隔：为超平面(w，b)关于T中所有样本点(xi，yi)的函数间隔最小值

定义几何间隔（geometrical margin）：点到超平面的距离

函数间隔y*(wx+b)=y*f(x)实际上就是|f(x)|，只是人为定义的一个间隔度量；而几何间隔|f(x)|/||w||才是直观上的点到超平面距离。

那么如果用向量表示，设w=(a,b),f(x)=wx+c,那么这个距离（几何间隔）正是|f(p)|/||w||。

现在我们希望能最大化这个间隔，目标函数可以定义为：
满足条件：
处于方便推导和优化的目的，我们可以令=1此时，上述的目标函数转化为(其中，s.t.，即subject to的意思，它导出的是约束条件)：

通过求解这个问题，我们就可以找到一个间隔最大的 分类器

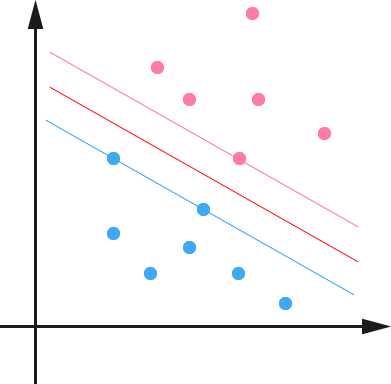
如图所示，中间的红色线条是超平面，另外两条线到红线的距离都是等于的(便是上文所定义的几何间隔，而我们上面得到的目标函数便是在相应的约束条件下，要最大化这个1/||w||值)。

支持向量的定义
可以看到两个支撑着中间的间隔的超平面，它们到中间的红线超平面的距离相等，即我们所能得到的最大的几何间隔，而“支撑”这两个超平面的必定会有一些点，而这些“支撑”的点便叫做支持向量Support Vector。
由于这些 supporting vector 刚好在边界上，所以它们满足
只有这些最接近超平面的点几何间隔值才为1，而离超平面越远，这些值越大。

深入SVM
轮到了怎么求解的问题

之前得到的目标函数（subject to导出的则是约束条件）：
上述问题等价于:

可以很明显地看出来，它是一个凸优化问题，或者更具体地说，它是一个二次优化问题——目标函数是二次的，约束条件是线性的。这个问题可以用任何现成的 QP (Quadratic Programming) 的优化包进行求解；通过 Lagrange Duality 变换到对偶变量 (dual variable) 的优化问题之后，可以应用拉格朗日对偶性进行求解，而且通常情况下这种方法比直接使用通用的 QP 优化包进行优化要高效得多。这样做的优点在于：一者对偶问题往往更容易求解；二者可以自然的引入核函数，进而推广到非线性分类问题。