最大似然估计（MLE）和最大后验概率（MAP）

最近在研究概率估计，最大似然估计（MLE）和最大后验概率（MAP）都可以用于估计生成样本数据的概率分布。

但二者略有区别，进行一下分析：

最大似然估计（MLE，Maximum Likelihood Estimation）

给定一堆数据，假如我们知道它是从某一种分布中随机取出来的，可是我们并不知道这个分布具体的参数，即“模型已定，参数未知”。例如，我们知道这个分布是正态分布，但是不知道均值和方差；或者是二项分布，但是不知道均值。 最大似然估计就可以用来估计模型的参数。MLE的目标是找出一组参数μ，使得模型产生出观测数据的概率最大，即：

其中P(X; μ)就是似然函数，表示在参数为μ的概率分布下，产生数据X的概率。我们假设每个观测数据是独立的，那么有

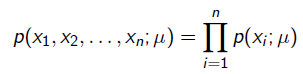
为了求导方便，一般对目标取log。 所以最优化似然函数等同于最优化对数似然函数，即：

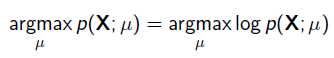
举一个抛硬币的简单例子。 现在有一个正反面不是很匀称的硬币，如果正面朝上记为H，方面朝上记为T，抛10次的结果如下：

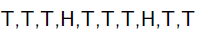
求这个硬币正面朝上的概率有多大？一个比较直接的结果是20%。

现在我们用MLE的思想去求解它。我们知道每次抛硬币都是一次二项分布，设正面朝上的概率是，那么似然函数为：

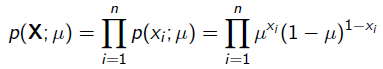
x=1表示正面朝上，x=0表示方面朝上。那么有：

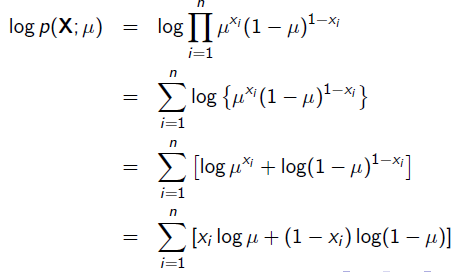
使用求导的方法求最优的μ值：

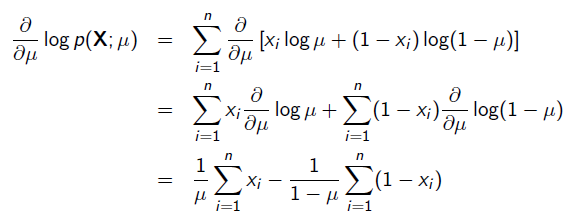
令导数为0，很容易得到：

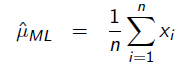
答案也就是0.2 。

然而，MLE估计不会把先验知识考虑进去，而且很容易造成过拟合现象。

举个例子，比如对癌症的估计，一个医生一天可能接到了100名患者，但最终被诊断出癌症的患者为5个人，在MLE估计的模式下我们得到的得到癌症的概率为0.05。

这显然是不太切合实际的，因为我们根据已有的经验，我们知道这种概率会低很多，这就是由于MLE估计没有把这种知识融入到模型里。

最大后验估计（MAP，Maximum A Posteriori Estimation）

假如上半部分的参数μ有一个先验概率呢？比如说，在上面抛硬币的例子，假如我们的经验告诉我们，硬币一般都是匀称的，也就是μ=0.5的可能性最大，μ=0.2的可能性比较小，那么参数该怎么估计呢？这就是MAP要考虑的问题。MAP优化的是一个后验概率，即给定了观测值后使μ概率最大：

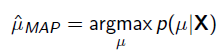
把上式根据贝叶斯公式展开：

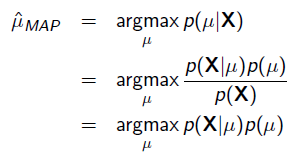
我们可以看出第一项P(X| μ)就是似然函数，第二项P(μ)就是参数的先验知识。取log之后就是：

这些先验信息无法从数据中获得（就像我们在上面举的癌症的例子），其实在上式中正好起到了正则化的作用，如：如果假设P(μ)服从高斯分布，则相当于加了一个L2范数；如果假设P(μ)服从拉普拉斯分布，则相当于加了一个L1范数。相比于MLE估计，先验附加信息有助于减少估计的方差，但是代价是增加了偏差。

部分内容来自于博客：

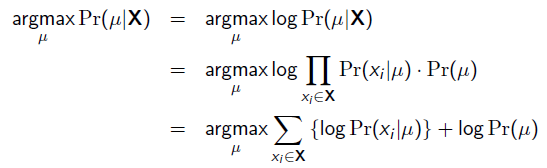
http://www.cnblogs.com/little-YTMM/p/5399532.html

https://www.cnblogs.com/sylvanas2012/p/5058065.html