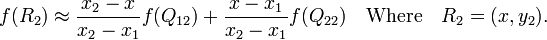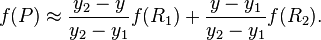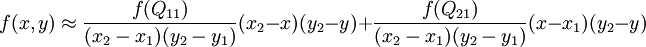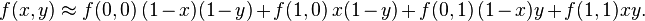双线性插值理论与代码实例

来源：互联网发布：网络成瘾的原因和影响编辑：程序博客网时间：2024/05/18 03:53

1. 双线性插值

假设源图像大小为mxn，目标图像为axb。那么两幅图像的边长比分别为：m/a和n/b。注意，通常这个比例不是整数，编程存储的时候要用浮点型。目标图像的第（i,j）个像素点（i行j列）可以通过边长比对应回源图像。其对应坐标为（i*m/a,j*n/b）。显然，这个对应坐标一般来说不是整数，而非整数的坐标是无法在图像这种离散数据上使用的。双线性插值通过寻找距离这个对应坐标最近的四个像素点，来计算该点的值（灰度值或者RGB值）。

若图像为灰度图像，那么（i，j）点的灰度值的数学计算模型是：

f(x,y)=b1+b2x+b3y+b4xy

其中b1,b2,b3,b4是相关的系数。关于其的计算过程如下如下：

如图，已知Q12，Q22，Q11，Q21，但是要插值的点为P点，这就要用双线性插值了，首先在x轴方向上，对R1和R2两个点进行插值，这个很简单，然后根据R1和R2对P点进行插值，这就是所谓的双线性插值。

clip_image001

双线性插值，又称为双线性内插。在数学上，双线性插值是有两个变量的插值函数的线性插值扩展，其核心思想是在两个方向分别进行一次线性插值。

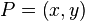假如我们想得到未知函数 $f$ 在点 $P=\left( x, y\right)$ 的值，假设我们已知函数 $f$ 在 $Q_{11} = \left( x_1, y_1 \right)$ , $Q_{12} = \left( x_1, y_2 \right)$ , $Q_{21} = \left( x_2, y_1 \right)$ , 及 $Q_{22} = \left( x_2, y_2 \right)$ 四个点的值。

首先在 x 方向进行线性插值，得到

$f(R_1) \approx \frac{x_2-x}{x_2-x_1} f(Q_{11}) + \frac{x-x_1}{x_2-x_1} f(Q_{21}) \quad\mbox{Where}\quad R_1 = (x,y_1),$

$f(R_2) \approx \frac{x_2-x}{x_2-x_1} f(Q_{12}) + \frac{x-x_1}{x_2-x_1} f(Q_{22}) \quad\mbox{Where}\quad R_2 = (x,y_2).$

然后在 y 方向进行线性插值，得到

$f(P) \approx \frac{y_2-y}{y_2-y_1} f(R_1) + \frac{y-y_1}{y_2-y_1} f(R_2).$

这样就得到所要的结果 $f \left( x, y \right)$ ,

$f(x,y) \approx \frac{f(Q_{11})}{(x_2-x_1)(y_2-y_1)} (x_2-x)(y_2-y) + \frac{f(Q_{21})}{(x_2-x_1)(y_2-y_1)} (x-x_1)(y_2-y)$

$+ \frac{f(Q_{12})}{(x_2-x_1)(y_2-y_1)} (x_2-x)(y-y_1) + \frac{f(Q_{22})}{(x_2-x_1)(y_2-y_1)} (x-x_1)(y-y_1).$

如果选择一个坐标系统使得 $f$ 的四个已知点坐标分别为 (0, 0)、(0, 1)、(1, 0) 和 (1, 1)，那么插值公式就可以化简为

$f(x,y) \approx f(0,0) \, (1-x)(1-y) + f(1,0) \, x(1-y) + f(0,1) \, (1-x)y + f(1,1) xy.$

或者用矩阵运算表示为

$f(x,y) \approx \begin{bmatrix}1-x & x \end{bmatrix} \begin{bmatrix}f(0,0) & f(0,1) \\f(1,0) & f(1,1) \end{bmatrix} \begin{bmatrix}1-y \\y \end{bmatrix}$

与这种插值方法名称不同的是，这种插值方法的结果通常不是线性的，它的形式是

b_{1}+b_{2}x+b_{3}y+b_{4}xy.\,

常数的数目都对应于给定的 f 的数据点数目

b_{1}=f(0,0)

b_{2}=f(1,0)-f(0,0)

b_{3}=f(0,1)-f(0,0)

b_{4}=f(1,1)-f(1,0)-f(0,1)+f(0,0)

线性插值的结果与插值的顺序无关。首先进行 y 方向的插值，然后进行 x 方向的插值，所得到的结果是一样的。

2.存在的问题

这部分的前提是，你已经明白什么是双线性插值并且在给定源图像和目标图像尺寸的情况下，可以用笔计算出目标图像某个像素点的值。当然，最好的情况是你已经用某种语言实现了网上一大堆博客上原创或转载的双线性插值算法，然后发现计算出来的结果和matlab、openCV对应的resize（）函数得到的结果完全不一样。

那这个究竟是怎么回事呢？

其实答案很简单，就是坐标系的选择问题，或者说源图像和目标图像之间的对应问题。

按照网上一些博客上写的，源图像和目标图像的原点（0，0）均选择左上角，然后根据插值公式计算目标图像每点像素，假设你需要将一幅5x5的图像缩小成3x3，那么源图像和目标图像各个像素之间的对应关系如下：

只画了一行，用做示意，从图中可以很明显的看到，如果选择右上角为原点（0，0），那么最右边和最下边的像素实际上并没有参与计算，而且目标图像的每个像素点计算出的灰度值也相对于源图像偏左偏上。

那么，让坐标加1或者选择右下角为原点怎么样呢？很不幸，还是一样的效果，不过这次得到的图像将偏右偏下。

最好的方法就是，两个图像的几何中心重合，并且目标图像的每个像素之间都是等间隔的，并且都和两边有一定的边距，这也是matlab和openCV的做法。如下图：

如果你不懂我上面说的什么，没关系，只要在计算对应坐标的时候改为以下公式即可，

int x=(i+0.5)*m/a-0.5

int y=(j+0.5)*n/b-0.5

instead of

int x=i*m/a

int y=j*n/b

利用上述公式，将得到正确的双线性插值结果

总结：

总结一下，我得到的教训有这么几条。

1.网上的一些资料有的时候并不靠谱，自己还是要多做实验。

2.不要小瞧一些简单的、基本的算法，让你写你未必会写，而且其中可能还藏着一些玄妙。

3.要多动手编程，多体会算法，多看大牛写的源码（虽然有的时候很吃力，但是要坚持看）。

源码：

void scale(Mat &srcmat, Mat &desmat, double sx, double sy){int nc = x, nl = y, srccol = 0, srcrow = 0;double alph = 0.0, beta = 0.0;for (int i = 0; i < nc; i++){uchar* desdata = desmat.ptr<uchar>(i);for (int j = 0; j < nl; j++){srcrow = int(i / sx);//下面的的几个if是判断放大后图像对应到原图像的坐标是否越界的if (srcrow >= srcmat.rows - 1){srcrow = srcmat.rows - 2;}alph = i / sx - srcrow;if (alph >= 1)alph = 1;srccol = int(j / sy);if (srccol >= srcmat.cols - 1)srccol = srcmat.cols - 2;beta = j / sy - srccol;if (beta >= 1)beta = 1;for (int k = 0; k < 3; k++){double kk = srcmat.at<Vec3b>(srcrow, srccol)[k] +beta*(srcmat.at<Vec3b>(srcrow, srccol + 1)[k] - srcmat.at<Vec3b>(srcrow, srccol)[k]);double jj = srcmat.at<Vec3b>(srcrow + 1, srccol)[k] +beta*(srcmat.at<Vec3b>(srcrow + 1, srccol + 1)[k] - srcmat.at<Vec3b>(srcrow + 1, srccol)[k]);desdata[j * 3 + k] = kk + alph*(jj - kk);}}}}//sx=1.2,sy=1.6

//图像基本信息输出int image_height = image.size().height;int image_width = image.size().width;cout << "Image Info: height:" << image_height << "  width:" << image_width << endl;//===============================================================================================================================//图像处理-----双线性插值cout << "Please input the Sx and Sy:" << endl;float Sx, Sy;cin >> Sx >> Sy;cout << "Sx = " << Sx << "; Sy = " << Sy << ";" << endl;Mat final_img;int final_img_height, final_img_width;final_img_height = image.size().height * Sx;final_img_width = image.size().width * Sy;final_img.create(final_img_height, final_img_width, CV_8UC1);int y, x;int x1, x2, y1, y2;float temp1, temp2;for (y = 0; y < final_img_height; y++){for (x = 0; x < final_img_width; x++){x1 = (int)(x / Sx);x2 = x1 + 1;y1 = (int)(y / Sy);y2 = y1 + 1;//判断边界if (y2 >= image_height || x2 >= image_width){final_img.at<uchar>(y, x) = image.at<uchar>(y1, x1);continue;}temp1 = (x2 - x / Sx) * image.at<uchar>(y1, x1) + (x / Sx - x1) * image.at<uchar>(y1, x2);temp2 = (x2 - x / Sx) * image.at<uchar>(y2, x1) + (x / Sx - x1) * image.at<uchar>(y2, x2);final_img.at<uchar>(y, x) = (uchar)((y2 - y / Sy) * temp1 + (y / Sy - y1) * temp2);}}//===============================================================================================================================//显示处理前后的图像namedWindow("original_image");imshow("original_image", image);namedWindow("final_image");cout << "Final image Info: height:" << final_img.size().height << "  width:" << final_img.size().width << endl;imshow("final_image", final_img);

//sx=1.2,sy=1.2

阅读全文

0 0