数据降维之PCA透彻讲解

来源：互联网发布：中国对外贸易数据分析编辑：程序博客网时间：2024/06/05 16:39

数据降维之PCA透彻讲解

数据降维之PCA透彻讲解
引言
PCA算法的数学基础
- 1 数据的向量表示及其基本运算
- 2 向量空间的基
- 3 基变换的矩阵表示
PCA算法的数学原理
- 1 方差
- 2 协方差
- 3 协方差矩阵
- 4 协方差矩阵对角化
PCA算法执行过程及其Java实现
- 1 PCA算法执行步骤
- 2 PCA算法的Java实现
PCA算法应用实例

0. 引言

　　
　　在做任何机器学习算法训练之前，无论该算法模型是分类、回归还是聚类，我们都需要从原始数据中提取数据特征，然后将提取的特征组合成特征向量的形式输入到模型中进行训练。但是现实中往往会存在这么一个问题：原始数据特征的维度特别高，不利于模型的训练。这时候我们需要对原始数据的特征向量进行降维处理，然后将降维后的数据输入到模型中进行训练，得出最终的训练模型。

　　PCA算法就是在这种需求之下产生的。它是专门用来对高维数据进行降维而设计的，通过将高维数据降维后得到的低维数能加快模型的训练速度，并且低维度的特征具有更好的可视化性质。但是有一点我们必须明确：降维或多或少地会带来一定的信息损失，因此我们在真正PCA算法的应用过程中一般需要设置一个损失阈值的方法来有效的控制信息的损失。

1. PCA算法的数学基础

　　PCA的理论基础建立在严格的线性代数矩阵分析之上。因此，为了让广大的算法爱好者都能够更好的理解PCA算法的工作原理。我们需要先温习一下与PCA算法相关的线性代数基础知识。

1.1 数据的向量表示及其基本运算

　　假设向量 A=(a1,a2,...,an)T 和 B=(b1,b2,...,bn)T，则两者的内积表示为如下计算：

A \cdot B = a 1 b 1 + a 2 b 2 + \dots + a n b n = \sum i = 1 n a i b i

内积运算将两个向量映射为一个实数。其计算方式非常容易理解，但是其意义并不明显。下面我们分析内积的几何意义。假设A和B是两个n维向量，我们知道n维向量可以等价表示为n维空间中的一条从原点发射的有向线段，为了简单起见我们假设A和B均为二维向量，则

A=(x1,y1)，

B=(x2,y2)。则在二维平面上A和B可以用两条发自原点的有向线段表示，见下图：
　　

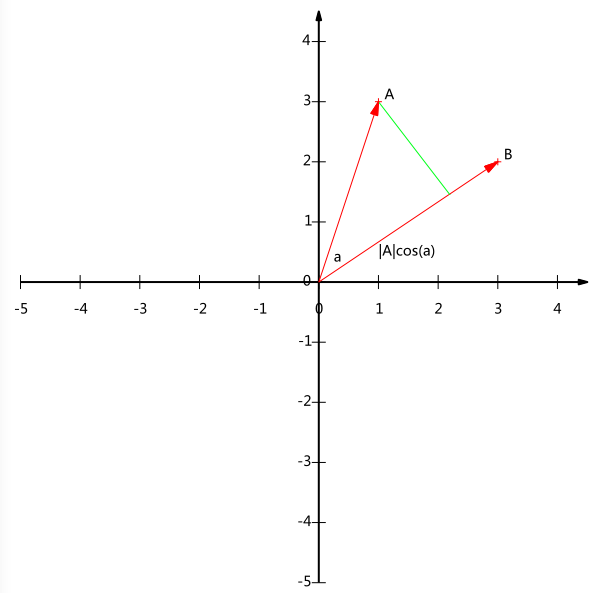
现在我们从A点向B所在直线引一条垂线。我们知道垂线与B的交点叫做A在B上的投影，再设A与B的夹角是 α，则投影的矢量长度为|A|=x21+y21‾‾‾‾‾‾‾√，其中|A|=x21+y21‾‾‾‾‾‾‾√是向量A的模，也就是A线段的标量长度。

注意这里我们专门区分了矢量长度和标量长度，标量长度总是大于等于0，值就是线段的长度；而矢量长度可能为负，其绝对值是线段长度，而符号取决于其方向与标准方向相同或相反。

到这里还是看不出内积和这东西有什么关系，不过如果我们将内积表示为另一种我们熟悉的形式：

A \cdot B = | A | \cdot | B | \cdot c o s (α)

现在事情似乎是有点眉目了：A与B的内积等于A到B的投影长度乘以B的模。再进一步，如果我们假设B的模为1，即让|B|=1|B|=1，那么就变成了：

A \cdot B = | A | \cdot c o s (α)

也就是说，设向量B的模为1，则A与B的内积值等于A向B所在直线投影的矢量长度！这就是内积的一种几何解释，也是我们得到的第一个重要结论。在后面的推导中，将反复使用这个结论。

1.2 向量空间的基

　　下面我们继续在二维空间内讨论向量。上文说过，一个二维向量可以对应二维笛卡尔直角坐标系中从原点出发的一个有向线段。例如下面这个向量：

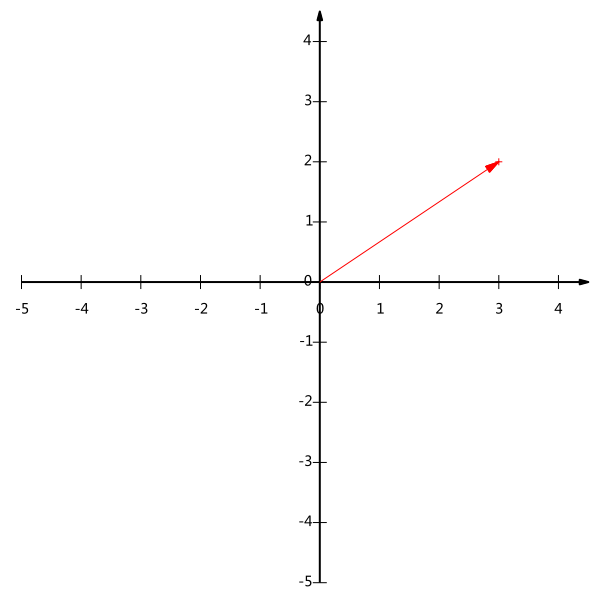
　　在代数表示方面，我们经常用线段终点的点坐标表示向量，例如上面的向量可以表示为(3,2)，这是我们再熟悉不过的向量表示。

　　不过我们常常忽略，只有一个(3,2)本身是不能够精确表示一个向量的。我们仔细看一下，这里的3实际表示的是向量在x轴上的投影值是3，在y轴上的投影值是2。也就是说我们其实隐式引入了一个定义：以x轴和y轴上正方向长度为1的向量为标准。那么一个向量(3,2)实际是说在x轴投影为3而y轴的投影为2。注意投影是一个矢量，所以可以为负。

更正式的说，向量(x,y)实际上表示线性组合：

x (1, 0)

阅读全文

0 0

中国对外贸易数据分析

原创粉丝点击