图的拉普拉斯矩阵学习-Laplacian Matrices of Graphs

We all learn one way of solving linear equations when we first encounter linear

algebra: Gaussian Elimination. In this survey, I will tell the story of some remarkable

connections between algorithms, spectral graph theory, functional analysis

and numerical linear algebra that arise in the search for asymptotically faster algorithms.

I will only consider the problem of solving systems of linear equations

in the Laplacian matrices of graphs. This is a very special case, but it is also a

very interesting case. I begin by introducing the main characters in the story.

1. Laplacian Matrices and Graphs. We will consider weighted, undirected,

simple graphs G given by a triple (V,E,w), where V is a set of vertices, E

is a set of edges, and w is a weight function that assigns a positive weight to

every edge. The Laplacian matrix L of a graph is most naturally defined by

the quadratic form it induces. For a vector x ∈ IRV , the Laplacian quadratic

form of G is：

Thus, L provides a measure of the smoothness of x over the edges in G. The

more x jumps over an edge, the larger the quadratic form becomes.

The Laplacian L also has a simple description as a matrix. Define the

weighted degree of a vertex u by：

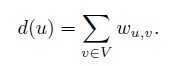
Define D to be the diagonal matrix whose diagonal contains d, and define

the weighted adjacency matrix of G by:

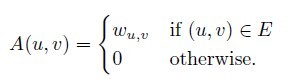
We have

L = D − A.

It is often convenient to consider the normalized Laplacian of a graph instead

of the Laplacian. It is given by D−1/2LD−1/2, and is more closely related to

the behavior of random walks.

Regression on Graphs. Imagine that you have been told the value of a

function f on a subset W of the vertices of G, and wish to estimate the

values of f at the remaining vertices. Of course, this is not possible unless

f respects the graph structure in some way. One reasonable assumption is

that the quadratic form in the Laplacian is small, in which case one may

estimate f by solving for the function f : V → IR minimizing f TLf subject

to f taking the given values on W (see [ZGL03]). Alternatively, one could

assume that the value of f at every vertex v is the weighted average of f at

the neighbors of v, with the weights being proportional to the edge weights.

In this case, one should minimize:

|D^-1Lf|

subject to f taking the given values on W. These problems inspire many

uses of graph Laplacians in Machine Learning.