计算点、线、面等元素之间的交点、交线、封闭区域面积和闭合集

来源：互联网发布：nginx 不能通过ip访问编辑：程序博客网时间：2024/05/17 04:57

地理信息系统软件开发中经常需要求取点、线、面之间的交点、交线、封闭区域面积和闭合集等结果，采用以矢量点乘和叉乘为基础的求取算法符合实际工作中已给出点位置和法向量等条件的情况，效率较高。

首先给出基本公式的推导。

矢量的结合率和交换率：

U+(V+W) = (U+V) + W;

U+V=V+U;

而设线段的起点和终点为P,Q;则中间任意一点R可以表示为:

R = P + r(Q - P); (0<r<1)

由P0,P1和P2三点构成的共面参数方程可表示为如下一种形式：

P(s,t) = (1-s-t)P0+sP1+tP2，其中s,t为参数

矢量的长度定义为：

设 V = (a,b); 则 |V| = sqrt(a*a + b*b); （即各轴数据平方和的开方）

而向量的规范化是 U = V/|V|，使得向量的长度为单位1。

矢量的点乘定义：

VW = v1w1+v2w2，V= (v1,v2) , W = (w1,w2);

此定义可从二维空间类推到三维和其他高次空间。

我们知道，二维平面上面一点P（x,y）在坐标轴转动某角度α后，新坐标为P(xnew,ynew)

设P点距离原点为r，此点与原X轴夹角为δ，则

x = rcosδ, y = rsinδ；

可求得新坐标为：xnew = rcos(δ-α)=rcosδcosα + rsinδsinα = xcosα + ysinα；

ynew =rsin(δ-α)=rsinδcosα –rcosδsinα = ycosα –xsinα；

下面推导广泛运用的一个公式：

VW = |V||W|cosϕ，ϕ为两向量的交角；

若V = (v1,0),既此点落在X轴上，则VW = v1w1 + 0w2 = v1w1；

因为V点落在轴上，则 |V| = v1,|W| cosϕ = w1；所以 VW = |V||W|cosϕ；

若为一般情况，即V= (v1,v2),则我们可旋转原始坐标轴角度δ后使得V点落在新X轴上，

由于： (v1w1 + v2w2)/|V| = w1cosδ+ w2sinδ = W点在新坐标系下的X轴数值 = |W| cosϕ

因此 v1w1 + v2w2 = |V||W|cosϕ；

在平时的运用中，计算cosϕ = VW / |V||W| ，可对两向量的交角大小进行判断，若VW为0，则说明两向量互相垂直；若VW大于0，则|ϕ|<90度，说明交角为锐角。

设向量V(a,b),对其旋转90度后，得到U= (acos90 + bsin90, ycos90-xsin90) = (b,-a)；可由此方法得到向量的垂直向量。

由VW = |V||W|cosϕ公式的推导中可以类推|V||W|sinϕ等于什么呢？推导如下：

|W|sinϕ = W点在新坐标系下的Y轴数值 = w2cosδ-w1sinδ= w2v1/|V|-w1v2/|V|=

(v1w2-v2w1)/|V|,即

v1w2-v2w1 = |V||W|sinϕ，ϕ为两向量的交角；

在平时的运用中，可采用此公式计算三角形和四边形的面积。也能判断两向量的位置关系，如果计算v1w2-v2w1为0，则说明两向量交角为0度或180度，即共线。如果计算结果大于0，则说明两向量交角0度到180度之间。

求取向量之间位置关系和三角形面积的参考代码：

// Input: three points P0, P1, and P2

// Return: >0 for P2 left of the line through P0 and P1

// =0 for P2 on the line

// <0 for P2 right of the line

double CDEMAlgorithm::isLeft( Point P0, Point P1, Point P2 )

{

return ( (P1.x - P0.x) * (P2.y - P0.y)

- (P2.x - P0.x) * (P1.y - P0.y) ); //叉乘

}

double CDEMAlgorithm::orientation2D_Triangle( Point V0, Point V1, Point V2 )

{

return isLeft(V0, V1, V2); //判断位置关系

}

double CDEMAlgorithm::area2D_Triangle( Point V0, Point V1, Point V2 )

{

return isLeft(V0, V1, V2) / 2.0; //求三角形的面积

}

double CDEMAlgorithm::dist3D_Line_to_Line( Line L1, Line L2)
{
Vector   u = L1.P1 - L1.P0;
Vector   v = L2.P1 - L2.P0;
Vector   w = L1.P0 - L2.P0;
double    a = Dot(u,u);        // always >= 0
double    b = Dot(u,v);
double    c = Dot(v,v);        // always >= 0
double    d = Dot(u,w);
double    e = Dot(v,w);
double    D = a*c - b*b;       // always >= 0
double    sc, tc;

// compute the line parameters of the two closest points
if (D < EPS) {         // 几乎平行
  sc = 0.0;
  tc = (b>c ? d/b : e/c);   //
}
else {
  sc = (b*e - c*d) / D;
  tc = (a*e - b*d) / D;
}

//sc,tc分别指示了在两条直线上的比例参数
Vector dP = w + (sc * u) - (tc * v); // = L1(sc) - L2(tc)

return sqrt(Dot(dP,dP)); // return the closest distance

}
附图:

继续上一节的内容，本节主要讲解三维空间中射线、线段与平面及三维物体的交点及距离的计算，它们在碰撞检测和可见性剔除等应用中是必不可少的。首先给出3D空间下点乘和叉乘的定义与定理的推导，再谈如何应用到程序编码的工作中。

设三维空间中任意两矢量V(v1，v2，v3)和W(w1，w2，w3)

由三角形的余弦公式：

cosα = (a2 + b2 – c2)／2ab

则两矢量夹角α的余弦： cosα = {(v1*v1 + v2*v2 + v3*v3) + (w1*w1+w2*w2+w3*w3)－ [ (w1 － v1)2+( w2 － v2)2+( w3 － v3)2] } / 2 |V| |W| = (v1w1+ v2w2 + v3w3)/ |V| |W|

由于将矢量的点乘定义为： V·W = v1w1+ v2w2 + v3w3 ；

所以 |V| |W| cosα = V·W；

由上面的结论引申，可知道如果两矢量的点乘为0，则说明夹角α的余弦为0，即矢量的夹角是90度，互相垂直。

再来看两矢量的叉乘，与点乘的计算结果定义为一数值不同，叉乘的结果定义为另外一个矢量 U (u1，u2，u3) ，其中：

u1 = v2w3 － v3w2；

u2 = v3w1 － v1w3；

u3 = v1w2 － v2w1；

由这个定义我们来推导：

V·U = v1(v2w3 － v3w2) + v2(v3w1 － v1w3) + v3(v1w2 － v2w1) = v1v2w3 － v1 v3w2 + v2v3w1－v2 v1w3 + v3v1w2－v3 v2w1 = 0；两矢量的点乘为0，说明它们互相垂直。

W·U = w1(v2w3 － v3w2) + w2(v3w1 － v1w3) + w3(v1w2 － v2w1) = 0,说明它们也是互相垂直的。

在三维空间中，U与V、W都垂直，说明U是垂直与V与W构成的平面，也就是这个平面的法向量。

U虽然是矢量，但其模|U|依旧是一个数值，表明其长度。

|U|2 = u1*u1 + u2*u2 + u3*u3 = (v2w3 － v3w2)2+( v3w1 － v1w3)2+( v1w2 － v2w1)2；

同时考虑，在α是V、W两矢量的夹角条件下，(|V| |W|sinα)2= |V|2|W|2（1－cos2α）= |V|2|W|2 － |V|2|W|2cos2α = |V|2|W|2 － (V·W)2= (v1*v1 + v2*v2 + v3*v3)( w1*w1+w2*w2+w3*w3) － (v1w1+ v2w2 + v3w3)2

通过化解，可以得到一个数学等式，即：

（bz－cy）2+(cx－az)2+(ay－bx)2=（a2+b2+c2）（x2+y2+z2）－（ax+by+cz）2

所以 (v2w3 － v3w2)2+( v3w1 － v1w3)2+( v1w2 － v2w1)2 = (v1*v1 + v2*v2 + v3*v3)( w1*w1+w2*w2+w3*w3) － (v1w1+ v2w2 + v3w3)2；

即 |U|2 = (|V| |W|sinα)2

|U| = |V| |W|sinα

在完成三维空间的点乘和叉乘定义与公式推导后，可以直接运用结论到程序的编写中，这些结论包括利用点乘来求得夹角的余弦，利用点乘为0来求得垂直于某向量的另一向量，利用两向量的叉乘来求得平面的法向量，利用叉乘的模来求得三角形的面积等。

三维空间中点到直线、射线和线段的距离。即从点P作垂直于线段（P0,P1）的垂线，求得垂心T后，计算两点之间的距离。

设置T点为参数表达方式： T = P0 + t(P1 –P0)；将T点看作是从P0开始往P1移动的动态点，则矢量PT为PP0与P0T两个矢量之和，当PT垂直于P0P1时，利用两个矢量的点乘为0列等式，求得参数t的数值。

(PP0 + P0T) ·P1P0 = 0；

即（P－P0）·(P1 –P0) + t(P1 –P0) ·(P1 –P0) = 0;

t = - （P－P0）·(P1 –P0) / (P1 –P0) ·(P1 –P0)

可以看出分子是需要计算两个矢量的点乘，而分母是矢量P0P1点乘自身，即为模的平方。

double CDEMAlgorithm::dist_Point_to_Line( Point P, Line L)

{

Vector v = L.P1 - L.P0; //顶点相减得到矢量

Vector w = P - L.P0; //顶点相减得到矢量

double c1 = Dot(w,v); //两矢量的点乘

double c2 = Dot(v,v); //两矢量的点乘

double b = c1 / c2; //求得参数

Point Pb = L.P0 + b * v; //解得参数后，得到垂心位置

return d(P, Pb); //返回两点之间的距离

}

在前面两节探讨的基础上,利用已知空间顶点坐标情况下，以矢量点乘和叉乘为基础，继续讲解三维空间中两条直线之间的距离,二维平面上任意凸多边形的面积, 三维空间中凸多边形的面积等方面的应用和程序编写工作。

三维空间中两条直线之间的距离

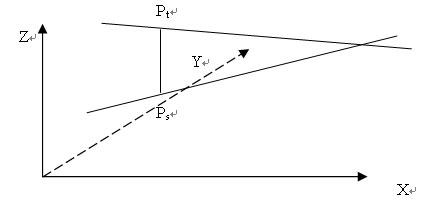
两条直线分别设置为P0P1，P2P3；

找到直线上的两个点Pt，Ps；Pt= P0 + t(P1 – P0) ；

Ps = P2 + s(P3 – P2) ；

两条直线之间的距离定义为它们之间的最短距离，可得知PtPs垂直于P0P1和P2P3。由上两节讲解得到的结论：两矢量互相垂直，则点乘为0，可得：

(Ps –Pt) •(P1 – P0) = 0；

(Ps –Pt) •(P3 – P2) = 0；

令U = P1 – P0；V = P3 – P2；则 (P2 + sU– P0 – tV) •U = 0；

(P2 + sU– P0 – tV) •V = 0；

再另W = P2 – P0；则 W•U + sU•U – tV•U = 0；

W•V + sU•V – tV•V = 0；

考虑到：U•U = |U|2

V•V = | V |2

V•U = U•V

解方程组，得系数：

s = ((W•V)( U•V) – (W•U) | V |2) / ( |U|2| V |2 – (U•V)2)

t = ((W•V) |U|2 – (W•U)( U•V) )/ (|U|2| V |2 – (U•V)2)

分母|U|2| V |2 – (U•V)2 若等于0，则说明两直线的夹角a的余弦为1，即两直线的夹角为0度，为互相平行。此时，不采用此公式计算，只需要在一条直线上任意取得一点，计算此点到另一直线的距离，即为两直线之间的距离。

参考代码：

double CDEMAlgorithm::dist3D_Line_to_Line( Line L1, Line L2)

{

Vector u = L1.P1 - L1.P0;

Vector v = L2.P1 - L2.P0;

Vector w = L1.P0 - L2.P0;

double a = Dot(u,u); // 点乘的结果

double b = Dot(u,v);

double c = Dot(v,v);

double d = Dot(u,w);

double e = Dot(v,w);

double D = a*c - b*b;

double sc, tc;

// 在我们已经推导后，计算参数

if (D < EPS) { // 两条线平行

sc = 0.0;

tc = (b>c ? d/b : e/c);

}

else {

sc = (b*e - c*d) / D;

tc = (a*e - b*d) / D;

}

//sc,tc分别指示了在两条直线上的比例参数

Vector dP = w + (sc * u) - (tc * v); //得到两顶点构成的矢量

return sqrt(Dot(dP,dP)); // 返回两顶点直接的距离

}

二维平面上任意凸多边形的面积

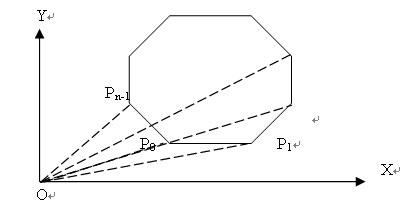
由上两节讲解得到的结论：P0x P1y – P0y P1x = | P0O | | P1O |sina，将此数值除以2，即得到三角形P0O P1的面积，在顶点依照顺或逆时针排好序后，依次计算每两个顶点与原点构成的三角形面积，由于面积带正负号（由方向决定的），求总和（将抵消一部分），最后得到多边形的面积。

参考代码：

// 输入: int n = 多边形的顶点个数

// Point* V = 记录 n+2 个顶点的数组

// with V[n]=V[0] and V[n+1]=V[1] //请注意在计算面积时，设置的顶点最后两个与最前两个重复

// 返回: 多边形的面积数值

double CDEMAlgorithm::area2D_Polygon( int n, Point* V )

{

double area = 0;

int i, j, k; // 索引

//(x0y1 - x1y0) + (x1y2 - x2y1) + (x2y3 - x3y2) ....

for (i=1, j=2, k=0; i<=n; i++, j++, k++) { //通过合并中间的项，可推出下面使用的公式计算面积（带符号）

area += V[i].x * (V[j].y - V[k].y);

}

return area / 2.0;

}

三维空间中凸多边形的面积

将多边形投影到某坐标面上，转换成2D平面的多边形面积问题后，将求得的投影面积再除以cosa，a为原始多边形与投影多边形的夹角。

参考代码：

// 参数：顶点N指示平面的法向量

double CDEMAlgorithm::area3D_Polygon( int n, Point* V, Point N )

{

double area = 0;

double an, ax, ay, az;

int coord;

int i, j, k;

// 选择法向量中的最大数值

ax = (N.x>0 ? N.x : -N.x); //绝对值

ay = (N.y>0 ? N.y : -N.y); //绝对值

az = (N.z>0 ? N.z : -N.z); //绝对值

coord = 3;

if (ax > ay) {

if (ax > az) coord = 1;

}

else if (ay > az) coord = 2; //平面的法向量的哪个轴数值最大，则准备在计算面积时候，投影到另外两根轴构成的平面上。

for (i=1, j=2, k=0; i<=n; i++, j++, k++)

switch (coord) { //首先计算二维投影平面上的面积

case 1:

area += (V[i].y * (V[j].z - V[k].z));

continue;

case 2:

area += (V[i].x * (V[j].z - V[k].z));

continue;

case 3:

area += (V[i].x * (V[j].y - V[k].y));

continue;

}

// 还原到原始面积

an = sqrt( ax*ax + ay*ay + az*az);

switch (coord) {

case 1:

area *= (an / ax);

break;

case 2:

area *= (an / ay);

break;

case 3:

area *= (an / az);

}

return area/2;

}

继续讲解3D空间下直线与平面的交点，点到平面的距离，直线到平面的距离，3D空间下两平面相交形成的交线等内容。求解过程中，未知顶点以参数方式表达，并依照矢量点乘和叉乘的性质列出方程求取结果，此技术思路符合实际工作中的初始条件，并且计算过程较快捷。

3D空间下直线与平面的交点

平面的已知条件为其法向量N（若法向量未知，可通过平面上任意两条直线矢量的叉乘求得），及其上任意一点Pon，直线的已知条件为其上两顶点P1，P2，现在要求此直线与平面的交点Pt，还是依照点乘与叉乘的定理这个思路来解决问题。

设 Pt = P1 + t(P2 ‐P1)；现在求取参数t的大小；

因为Pt也是平面上的顶点，则矢量Pt Pon与法向量的点乘为0，可列方程：

(Pt ‐Pon) • N = 0；

(P1 ‐Pon)• N + t(P2 ‐P1)• N = 0；

则 t = ‐(P1 ‐Pon)• N /(P2 ‐P1)• N；

若分母(P2 ‐P1)• N = 0，则说明直线垂直于法向量，与平面是平行的，将无交点。若分子(P1 ‐Pon)• N = 0，则说明直线上的顶点与平面上顶点构成的向量垂直于法向量，即此顶点为交点或这个直线位于平面上。

参考代码

// 输入: 直线上的两个顶点p1, p2；平面的法向量和其上任意一顶点 pNormalofPlane

// 输出: 若存在的话，输出直线与平面的交点 *I0

// Return: 0 代表没有交点

// 1 代表存在唯一的交点 *I0

// 2 代表直线上顶点为交点或整个直线位于平面上

int CDEMAlgorithm::Intersect3D_LinePlane( XYZ p1,XYZ p2, XYZ pNormalofPlane, XYZ pOnPlane,XYZ* I )

{ Vector u = p2 - p1;

Vector w = p1 - pOnPlane;

double D = Dot(pNormalofPlane, u); //点乘

double N = -Dot(pNormalofPlane, w); //点乘

if (fabs(D) < EPS) { // 直线与平面平行

if (N == 0) // 顶点为交点或这个直线位于平面上

return 2;

else

return 0; // 交点不存在

}

double t = N / D;

*I = p1 + t*(p2 - p1); // compute segment intersect point

return 1;

}

点到平面的距离

点到平面的距离问题可转化为首先求垂心，再求两顶点之间的距离。

平面的已知条件为其法向量N，及其上任意一点Pon，已知一顶点P1，现在要求此顶点到平面的垂线交点Pt，

因为矢量PtP1垂直与平面，而垂直于平面的法向量为N，所以可将Pt设定为：

Pt = P1 + tN；现在求取参数t的大小；

因为Pt也是平面上的顶点，则矢量Pt Pon与法向量的点乘为0，可列方程：

(Pt ‐Pon) • N = 0；

(P1 ‐Pon)• N + tN• N = 0；

则 t = ‐(P1 ‐Pon)• N /N• N；

若分子(P1 ‐Pon)• N = 0，则说明顶点与平面上顶点构成的向量垂直于法向量，即此顶点位于平面上，Pt = P1。

参考代码与上面介绍的函数类似。

3D空间下直线到平面的距离

有前面介绍的内容后，求取3D空间下直线到平面的距离变得容易，在判断直线不完全落在平面上或与出现与平面相交的情况后，即此直线将与平面平行。取直线上任意一顶点，按照介绍的点到平面的距离方法，可求得直线到平面的距离。

      3D空间下两平面相交，一般形成交线。

交线既同时属于两个平面，则垂直于这两个平面的法向量，计算两个法向量的叉乘（前面已经证明，叉乘形成的矢量垂直于此两矢量），即为这条交线的方向。再找到这条交线上的一个顶点，可确定直线方程。

设两平面上的已知顶点为Ps，Pt，法向量为U，V，要寻找的交线上的顶点为Pw，由于平面上的顶点相减得到的矢量与法向量点乘为0，有方程组：

( Pw ‐ Ps)• U = 0

( Pw ‐ Pt)• V = 0

此方程组含有两个方程，但3个未知数（Pw的x，y，z轴数值），可令其中一个数值为0，从而求解方程组，得到另外两个未知数。

不妨设z = 0，可求得，

x = (V y Ps•U－Uy Pt•V) /(UxVy－ VxUy)；

y = (V x Ps•U－Ux Pt•V) /(UyVx－ VyUx)；

z = 0；

从几何上解释是，此顶点就是两平面和平面Z=0 交点。若两平面中有与平面Z=0情况出现，可以调整为与平面X = 0或Y = 0相交。

参考代码

// 输入: 两个平面，分别指定一个顶点和法向量

// 输出 : 若存在的话，将输出一条直线

// Return: 0 表示没有交线

// 1 表示两个平面共面

// 2 表示能得到一条唯一的交线

int CDEMAlgorithm::Intersect3D_2Planes( XYZ pNormalofPlane1, XYZ pOnPlane1, XYZ pNormalofPlane2, XYZ pOnPlane2, XYZ Linep1,XYZ Linep2 )

{

XYZ u;

u.x = pNormalofPlane2.y * pNormalofPlane1.z - pNormalofPlane2.z*pNormalofPlane1.y; u.y = pNormalofPlane2.x * pNormalofPlane1.z - pNormalofPlane2.z*pNormalofPlane1.x;

u.z = pNormalofPlane2.x * pNormalofPlane1.y - pNormalofPlane2.y*pNormalofPlane1.x; //以上三步，求得两个法向量的叉乘，即交线的方向矢量

double ax = (u.x >= 0 ? u.x : -u.x); //取正数

double ay = (u.y >= 0 ? u.y : -u.y);

double az = (u.z >= 0 ? u.z : -u.z);

//检测两平面是否能有交线

if ((ax+ay+az) < EPS) {

// 检测是共面还是平行

XYZ v = VectorSub(pOnPlane2,pOnPlane1);//将两平面上的已知顶点相减

if (Dot(pNormalofPlane1, v) == 0) //两平面上的顶点相减，形成的矢量与法向量垂直，说明共面

return 1; // 两平面是共面的

else

return 0; // 两平面是平行的，没有交线

}

int maxc;

if (ax > ay) {

if (ax > az)

maxc = 1;

else maxc = 3;

}

else {

if (ay > az)

maxc = 2;

else maxc = 3;

} //以上工作是：找到叉乘向量中的最大分量

// 找到两个平面形成的交线上的一点

// 让三个未知数中的一个为0，求另外两轴的未知数

XYZ iP; // 将要求得的顶点

double d1, d2;

d1 = -Dot(pNormalofPlane1, pOnPlane1); // 为前面分析工作中的 - Ps•U

d2 = -Dot(pNormalofPlane2, pOnPlane2); // 为前面分析工作中的 - Pt•V

switch (maxc) { // 根据最大的分量来确定哪根轴的数值为0

case 1: // 与x=0平面相交

iP.x = 0;

iP.y = (d2*pNormalofPlane1.z - d1*pNormalofPlane2.z) / u.x;

iP.z = (d1*pNormalofPlane2.y - d2*pNormalofPlane1.y) / u.x;

break;

case 2: // 与 y=0平面相交

iP.x = (d1*pNormalofPlane2.z - d2*pNormalofPlane1.z) / u.y;

iP.y = 0;

iP.z = (d2*pNormalofPlane1.x - d1*pNormalofPlane2.x) / u.y;

break;

case 3: // 与 z=0平面相交

iP.x = (d2*pNormalofPlane1.y - d1*pNormalofPlane2.y) / u.z;

iP.y = (d1*pNormalofPlane2.x - d2*pNormalofPlane1.x) / u.z;

iP.z = 0;

}

Linep1 = iP; //交线上的一个顶点

Linep2 = VectorAdd(iP , u); //交线上的另外一个顶点

return 2;
}

平面上点与多边形包含关系的查询。

查询平面上一点是否在某多边形（可以为凸或凹多边形）范围内，或在其边上，或在范围之外，此方法作为GIS空间分析中的一种有广泛的应用。

具体方法之一是从此点开始沿任意方向作射线，计算此射线与多边形的边的相交个数，由于相交能说明点进出多边形的次数，若为偶数，则在多边形范围之外，为奇数则点被包含在多边形之内。为计算方便，常将射线方向定为与X或Y轴平行。

参考代码:
// 输入: 顶点 P

// 多边形的顶点数组 V[ ]，顶点个数为n+1 ，其中 V[n]=V[0]

// 返回的数值: 0表示在多边形之外, 1 表示在多边形之内

int CDEMAlgorithm::cn_PnPoly(Point P, Point* V,int n )//判断一个点和多边形的包含关系{

int cn = 0; // 记录相交个数

//对每条边进行循环

for (int i=0; i<n; i++) { // 由V[i] 和 V[i+1]顶点构成的边

if (((V[i].y <= P.y) && (V[i+1].y > P.y))||((V[i].y > P.y) && (V[i+1].y <= P.y))) { //说明要判断的这个顶点Y数值在多边形这条边的两个端点Y轴数值之间

double vt = (P.y - V[i].y) / (V[i+1].y - V[i].y); //计算系数，数值在0到1之间

if (P.x < V[i].x + vt * (V[i+1].x - V[i].x)) //说明此顶点在平行于X轴的平行线：y=P.y和与此条边的交点的右侧

++cn; //说明要判断的这个顶点与多边形这条边是相交的，计数器加1

}

} //循环结束

if (cn % 2 == 0) return 0;

else return 1; //若为偶数则说明在多边形的范围外，若为奇数说明在范围内

}

方法之二是判断此点与多边形边的左右邻接关系。这需要使用前面讲解的矢量XY数值交叉相乘从而判断夹角正弦的方法。

此图说明顶点一进一出多边形的情况。

由于多边形范围外的顶点将一进一出，有抵消，最后的计算结果为0就说明顶点在范围之外，其他返回的计算结果都表明在范围之内。

参考代码：

int CDEMAlgorithm::wn_PnPoly( Point P, Point* V, int n )//判断点和多边形范围的关系

{

int wn = 0; // 计数器

for (int i=0; i<n; i++) { //对每条边进行循环，其顶点为 V[i] 和 V[i+1]
if (V[i].y <= P.y) {

if (V[i+1].y > P.y) //P点的Y轴数值在一条上升边（Y轴数值增大）的范围内

if (isLeft( V[i], V[i+1], P) > 0) //调用前面章节讲解的isLeft()函数，来通过sina 的正负判断点P在此条边的左端

++wn; //如上图中靠右边的那种情况

}

else { //点的Y轴数值在一条下降边（Y轴数值减小）的范围内

if (V[i+1].y <= P.y)

if (isLeft( V[i], V[i+1], P) < 0) //通过sina 的正负可以判断点P在边的右端

--wn; //如上图中靠左边的那种情况

}

} //循环结束

return wn; //由于多边形范围外的顶点将一进一出，有抵消，最后的计算结果为0就说明顶点在范围之外，其他返回的计算结果都表明在范围之内。

}

单调链的说明: 对于折线L = {p1，p2，p3，…，pn}，xi是pi的横坐标，若xi<=xi+1，或xi>=xi+1，则称折线为关于x轴的单调增(或减)链。同样，对于y轴也适用。

平面上多条线段求交问题。
对于平面上的N条线段，若使用最直接的方法，即两两求其交点，则(N-1) + (N-2)+…1 = N(N-1)/2次运算，时间复杂度是O(n2)。这种方法对交点个数接近N(N-1)/2的情况可行，但大多数情况下，N条线段形成的交点个数是较少的，此时算法可调整成与输入线段个数和输出的交点个数相关的效率更高的方法，如Bentley-Ottmann 算法。

算法的思路是，以X轴升序构造顶点队列和初始化扫描线链表后,对顶点队列中所有元素开始循环:
当取出的元素为线段的左端点时，首先将此条线段插入到扫描线段链表中，同时以Y轴的升序重排链表中所有元素，然后分别计算此条线段与扫描线段链表中上下相邻线段的相交情况，若有交点，则将交点插入到顶点队列中。

当取出的元素为线段的右端点时，首先将此条线段从扫描线段链表中删除，然后计算此时与此条线段上下相邻的那两条线段之间的相交情况，如果有交点，但在顶点队列中还不存在，则将其插入顶点队列。

当取出的元素为交点时，首先将这个交点增加到最后要输出的结果集合中。然后得到这个交点从属的两条线段，交换它们在扫描线链表中的位置后，分别与新邻接的线段求交点，如果有交点，但在顶点队列中还不存在，则将其插入顶点队列。

以上3种情况分别处理后，从顶点队列中移走这个取出的元素。

当循环处理完毕，结果集合中的元素即为所有的交点。

这种方法最后以一次循环取代了最直接的两两线段求交点的两次循环。不过，需要注意的是，当交点个数接近n2级别时，Bentley-Ottmann算法的效率比直接两两求其交点的方法低下。

参考代码：

int intersect_Polygon( Polygon Pn )

{

EventQueue Eq(Pn); //顶点队列

SweepLine SL(Pn); //扫描线链表

Point e; // 当前的顶点

SLseg* s; // 当前的线段

Point singlepoint; //准备求得的交点

PointList PL; //所有求得的交点保存在其中

while (Eq != EMPTY) //循环开始，直到队列为空

{

e = Eq->next(); //得到开头顶点元素

if (e->type == LEFT) { // 当为线段的开始顶点

s = SL.add(e); // 增加此顶点所属的线段到扫描线链表中

if (SL.intersect( s, s->above, singlepoint)) //判断此顶点所属的线段与处于其上的线段是否相交

{

Eq->insert(singlepoint); // 插入交点到顶点队列中

SL.record(s, s->above, singlepoint);//在扫描线链表中记录此交点的上下线段

}

if (SL.intersect( s, s->below, singlepoint))

Eq->insert(singlepoint); // 插入交点到顶点队列中

}

else if(e->type == RIGHT) //当为线段的结束顶点

{

s = SL.find(e); // 从扫描线链表中找到此顶点所属的线段

if (SL.intersect( s->above, s->below,singlepoint)) //判断此线段的上下两相邻线段是否相交

if(Eq->find(singlepoint) == false) //如果求得的交点还不存在于顶点队列中

Eq->insert(singlepoint) //插入这个新求的交点到顶点队列中

SL.remove(s); // 从扫描线链表中移走此顶点所属的线段

}

else //当为交点

{

PL.add(e); //保存结果到最后的输出集合中

SLseg* sE1 = SL.findrecord(e,ABOVE);//得到此交点在扫描线链表中的第一条线段

SLseg* sE2 = SL.findrecord(e,BELOW);//得到此交点在扫描线链表中的第二条线段

SL.swap(sE1,sE2); //交换两条线段在链表中的位置，从几何上可看作：通过顶点后，两条线段的上下位置关系交换

if (SL.intersect( sE2, sE2->above,singlepoint)) //判断新的上下两相邻线段是否相交

if(Eq->find(singlepoint) == false) //如果求得的交点还不存在于顶点队列中

Eq->insert(singlepoint) //插入这个新求的交点到顶点队列中

if (SL.intersect( sE1, sE1->below,singlepoint)) //判断新的上下两相邻线段是否相交

if(Eq->find(singlepoint) == false) //如果求得的交点还不存在于顶点队列中

Eq->insert(singlepoint) //插入这个新求的交点到顶点队列中

}

Eq->remove(e); //此元素处理完毕，将其弹出

}

return 1;

}

平面上顶点集合的包围容器

寻找几何物体（点、线段、面与体等）的包围容器（Bounding Container）能加速三维仿真程序中的光线跟踪、碰撞检测和消隐处理等过程，因为在使用这些复杂的处理方法前，采用一个包围容器的预处理能先剔除一些不需参加后续计算的几何物体。包围容器的形状分为矩形、多边形和椭圆等，需注意计算这个容器所消耗的时间应小于希望节省的时间。

以多边形包围容器为例，寻找每条边，划分空间为两部分，最后各个部分的交集为所求容器。

Fi(X, Y) = aiX + biY +ci <=0 (i = 1,2 …k) (二维)

Fi(X, Y, Z) = aiX + biY +ciZ + di <=0 (i = 1,2 …k) (三维)

若容器为一正规的矩形或长方体，即各条边平行于轴，可通过比较顶点的各轴数值大小，求得最小值(Xmin, Ymin, Zmin)和最大值(Xmax, Ymax, Zmax)，以X=Xmin，X= Xmax，Y=Ymin，Y=Ymax，Z=Zmin, Z=Zmax等平面划分空间，最后构成的交集为所求包围容器。

若希望矩形或长方体容器各条边不用平行于轴，可构建X±Y或X±Y±Z表达式来划分空间。

将各顶点数据代入表达式，经比较求得Cmin、Cmax、dmin和dmax等系数。对三维空间数据同样处理，求四个表达式X±Y±Z的8个系数。

顶点集合Q的凸包(Convex Hull)是指存在一个最小凸多边形，使得Q中的点在这个多边形的边上或者在其范围内。

求凸包有很多方法，将在随后章节讲解。

若包围容器的形状为球体（在二维平面上是圆）的话，第一步可通过顶点初始化一个球体，在考虑新顶点加入的时候，如果将新顶点包含在范围内，则球体保持不变。如果新顶点位于范围之外，则考虑如何改变球心和增大半径。许多算法考虑是如何使得这种改变最小化。以下介绍的是一种快速、简单和近似的改变方法，即连接新顶点和原球心，以这两顶点距离加上原半径构成新直径，直径上中点为新圆心。

参考代码：

// 输入: n个顶点的数组V[]

// 输出: 包围圆的圆心和半径

void CDEMAlgorithm::fastBall( Point V[], int n, Ball* B)

{

Point C; // 圆心

double rad; //半径

double radTwo; // 半径的平方

double xmin, xmax,ymin,ymax; // 包围盒的顶点坐标

int Pxmin,Pxmax,Pymin,Pymax; //包围盒的顶点的索引

// 寻找最小和最大数值

xmin = xmax = V[0].x;

ymin = ymax = V[0].y; //赋第一个顶点的数值

Pxmin = Pxmax = Pymin = Pymax = 0;

for (int i=1; i<n; i++) {

if (V[i].x < xmin) {

xmin = V[i].x;

Pxmin = i; //记录索引

}

else if (V[i].x > xmax) {

xmax = V[i].x;

Pxmax = i; //记录索引

}

if (V[i].y < ymin) {

ymin = V[i].y;

Pymin = i; //记录索引

}

else if (V[i].y > ymax) {

ymax = V[i].y;

Pymax = i; //记录索引

}

// 以最大数值初始化圆

Vector dVx = V[Pxmax] - V[Pxmin]; // X轴的最大跨度

Vector dVy = V[Pymax] - V[Pymin]; // Y轴的最大跨度

double dx2 = Dot(dVx,dVx); // X轴的最大跨度的平方

double dy2 = Dot(dVy,dVy); // Y轴的最大跨度的平方

if (dx2 >= dy2) { // X轴的最大跨度的平方大于Y轴的最大跨度的平方

C = V[Pxmin] + (dVx / 2.0); // 设置圆心的位置

radTwo = Dot(V[Pxmax] - C,V[Pxmax] - C); //半径的平方

}

else { // Y轴的最大跨度的平方大于X轴的最大跨度的平方

C = V[Pymin] + (dVy / 2.0); //设置圆心的位置

radTwo = Dot(V[Pymax] - C,V[Pymax] - C); //半径的平方

}

rad = sqrt(radTwo); //半径

// 对初始圆扩展

Vector dV;

double dist, dist2;

for (int i=0; i<n; i++) {

dV = V[i] - C; //新顶点与圆心的矢量差

dist2 = Dot(dV,dV);

if (dist2 <= radTwo) // 新顶点位于圆内

continue;

//新顶点不在圆内，需扩展圆

dist = sqrt(dist2); //新顶点和圆心之间的距离

rad = (rad + dist) / 2.0; //改变半径

radTwo = rad * rad;

C = C + ((dist-rad)/dist) * dV; // 新圆心的位置，从原圆心沿矢量差移动

}

B->center = C; //赋圆心

B->radius = rad; //赋半径

return;
}

介绍求取平面上顶点集合凸包的Graham Scan和Andrew's Monotone Chain方法。基本原理是在顶点排序好后，初始化一栈，循环取出顶点集合中每个顶点元素，将其与栈顶两元素进行判别，看是否符合凸包条件，循环结束后，栈中剩余元素即为所求。具体过程如下。

求凸包Graham Scan方法。它的大致过程是：
       找到最右下顶点P0后，以各顶点与P0X的夹角来排序所有的集合中顶点。实际工作中，可简化角度计算工作，而通过前面章节介绍的isLeft()函数，来判断顶点P2是否处于线段P0P1左边，从而判断夹角的大小。设这些经过排序的顶点为P0，P1，…Pn-1；
    邻接关系判断图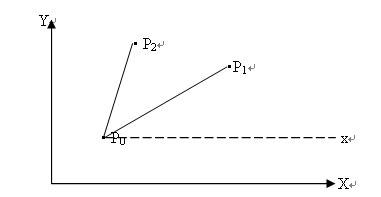


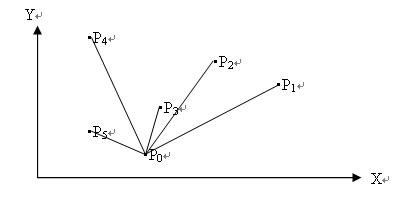
         将顶点排好序
    然后，建立一个栈，最开始时P0，P1进栈，对于剩下的顶点P2，P3，…Pn-1等依次取出，若栈顶的开头两个顶点与新取出的顶点不满足“左转”（即isLeft()函数返回数值大于0）条件，则将栈顶的第一个顶点出栈，继续测试，直到满足“左转”条件后将新取出的顶点进栈；所有剩下的顶点P2，P3，…Pn-1处理完之后栈中剩下的顶点构成凸包。

需说明的是，此方法很难推进到三维空间。

参考代码：

//主程序

Stack GrahamScan( )

{

Stack top;

int i;

Point p1, p2;

top = NULL;

top = Push ( &P[0], top );

top = Push ( &P[1], top ); //初始化栈

i = 2;

while ( i < n ) //对所有的排序后顶点循环

{

if( !top->next) printf("Error"n"); //栈中没有第二个元素，报出错信息

p1 = top->next->p;

p2 = top->p; //取出栈顶的两个元素

if ( isLeft( p1->v , p2->v, P[i].v ) )//判断是否左转

{

top = Push ( &P[i], top ); //压栈

i++; //顶点计数器增加

}

else

top = Pop( top ); //退栈

}

return top; //栈中剩下的元素即为构成凸包的顶点

}

//开始准备工作中寻找所有顶点中右下角顶点

int FindLowest( void )

{

int i;

int m = 0;

for ( i = 1; i < n; i++ ) //对所有顶点循环

if ( (P[i].v[Y] < P[m].v[Y]) ||

((P[i].v[Y] == P[m].v[Y]) && (P[i].v[X] > P[m].v[X])) )

m = i;

return m; //返回右下角最低点索引

}

求凸包Andrew's Monotone Chain方法。

首先，依X轴和Y轴数值顺序排列所有顶点。

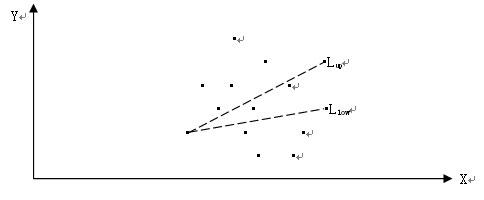
以最左(当X轴数值相同的时候，以Y轴数值最下和最上取顶点)至最右边的顶点(当X轴数值相同的时候，以Y轴数值最下和最上取顶点)连线，构成Lup，Llow等线段，将顶点集合分成上下两部分，分别使用类似于上面介绍的Graham Scan方法寻求子凸包，最后合并形成一个凸包（注意连接处顶点的重复存储）。

参考代码：

// 输入经过排序的顶点数组 P[]，n为数组中顶点个数

// 输出: 凸包的顶点集合 H[]

// 返回: H[]中的顶点个数

int CDEMAlgorithm::chainHull_2D( Point* P, int n, Point* H )

{

// 输出的数组H[]被用作一个栈

int bot=0, top=(-1); // 指示栈底和栈顶

int i;

int minmin = 0, minmax; // 得到X轴最小情况下Y轴分别最小和最大顶点的索引

double xmin = P[0].x;

for (i=1; i<n; i++)

if (P[i].x != xmin) break; //顶点已经排好序，搜索开始阶段的X轴最小值

minmax = i-1; //记录X轴最小情况下Y轴最大顶点的索引

if (minmax == n-1) { // 如果出现极端情况，即所有顶点X轴数值都最小

H[++top] = P[minmin];

if (P[minmax].y != P[minmin].y) // 如果两顶点的Y轴数值不等，则可构成线段

H[++top] = P[minmax];

H[++top] = P[minmin]; // 将这两个顶点增加到输出的数组中

return top+1; //返回输出的数组中的顶点个数

}

int maxmin, maxmax = n-1; // 得到X轴数值最大情况下 Y轴数值分别最小和最大的顶点索引

double xmax = P[n-1].x;

for (i=n-2; i>=0; i--) //从顶点的原始数组中反向循环，因为顶点已排好序

if (P[i].x != xmax) break;

maxmin = i+1; //记录X轴数值最大情况下Y轴数值最小的顶点索引

H[++top] = P[minmin]; // 开始计算下半部分凸包，首先将X轴和Y轴数值都最小的顶点压入栈

i = minmax; //从X轴数值最小情况下Y轴数值最大的顶点开始计数

while (++i <= maxmin)

{

// 以X轴和Y轴数值最小顶点连接X轴最大和Y轴数值最小顶点建立低线

if (isLeft( P[minmin], P[maxmin], P[i]) >= 0 && i < maxmin)

continue; // 由于此顶点位于这根低线之上，所以忽略，继续下次循环

while (top > 0) // top是从最开始的-1计数，所以大于0的话，表明栈中至少有2个元素

{

if (isLeft( H[top-1], H[top], P[i]) > 0)

break; //表明P[i]顶点是需要的凸包中新顶点，结束循环

else

top--; //将栈顶元素出栈，继续循环

}

H[++top] = P[i]; // 将顶点P[i]压入栈

}

// 下面，计算上半部分的凸包顶点集合

if (maxmax != maxmin) // 如果X轴数值最大情况下Y轴有不同顶点存在

H[++top] = P[maxmax]; // 将X轴数值与Y轴数值最大的顶点压入栈

bot = top; // 记住准备增加元素到栈前已经存在的元素个数

i = maxmin; //从X轴数值最大情况下Y轴数值最小的顶点开始计数

while (--i >= minmax)

{

// 以X轴和Y轴数值最大顶点连接X轴最小和Y轴数值最大顶点建立高线

if (isLeft( P[maxmax], P[minmax], P[i]) >= 0 && i > minmax)

continue; // 由于此顶点位于这根高线之下，所以忽略，继续下次循环

while (top > bot) // top还是比开始记住的bot大，表明栈中至少有2个元素

{

if (isLeft( H[top-1], H[top], P[i]) > 0)

break; //表明P[i]顶点是需要的凸包中新顶点，结束循环

else

top--; //将栈顶元素出栈，继续循环

}

H[++top] = P[i]; // 将顶点P[i]压入栈

}

if (minmax != minmin) //如果X轴数值最小情况下Y轴有不同顶点存在

H[++top] = P[minmin]; // 把这最后一个顶点压入栈

return top+1; //返回输出的凸包数组中的顶点个数

}

现在介绍平面上顶点集合凸包的Bentley-Faust-Preparata (BFP)方法，与前面讲解的Graham Scan和Andrew's Monotone Chain方法不同之处是，预先并不需要将整个顶点集合一起按照X、Y轴数值排序。这种方法虽然是种近似方法，但时间复杂度降低，对于大数据量顶点的处理要求比较适合。

基本方法是，取代整个顶点集合的依次X、Y轴排序，而首先依X轴数值大小划分几个区间，在每个区间中找到Ymin，Ymax顶点，以所有区间的这些顶点为预选，采用Andrew's Monotone Chain算法中使用过的“左转”方式来判断凸包条件是否成立，最后构成上下两个凸包子集，将其合并得到结果。其近似的原因是，每个区间可能不只有Ymin，Ymax等顶点作为预选。倘若将区间数量增大，则算法的准确性上升。

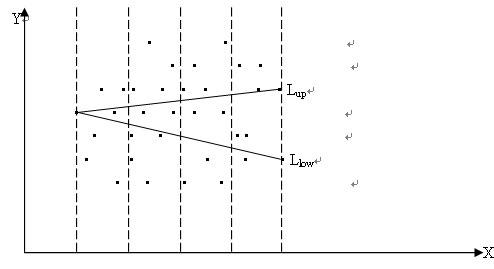
参考代码：

// 输入: 没有排序的顶点数组P[]，数组中的顶点个数n，准备将X轴分开成 k个区间

// 输出: 生成的凸包顶点集合H[]

// 返回的数值: 凸包H[]中的顶点个数

int CDEMAlgorithm::nearHull_2D( Point* P, int n, int k, Point* H )

{

int minmin=0, minmax=0; //准备记录X轴数值最小情况下Y轴数值最小和最大顶点索引

int maxmin=0, maxmax=0; //准备记录X轴数值最大情况下Y轴数值最小和最大顶点索引

double xmin = P[0].x, xmax = P[0].x; //初始化X轴最小和最大数值

Point* cP; // 被处理的顶点

int bot=0, top=(-1); // 指示栈底和栈顶

for (int i=1; i<n; i++) { //对所有顶点循环处理

cP = &P[i];

if (cP->x <= xmin) {

if (cP->x < xmin) { // 有更小的X轴数值出现

xmin = cP->x;

minmin = minmax = i; //记录下顶点索引

}

else { // 若相同的X轴最小数值出现

if (cP->y < P[minmin].y)

minmin = i; //记录下顶点索引，此时Y轴更小

else if (cP->y > P[minmax].y)

minmax = i; //记录下顶点索引，此时Y轴更大

}

if (cP->x >= xmax) { // 有更大或相同的X轴数值出现

if (cP->x > xmax) { // 有比xmax还大的顶点出现

xmax = cP->x;

maxmin = maxmax = i; //记录顶点索引

}

else { //若相同的X轴最大数值出现

if (cP->y < P[maxmin].y)

maxmin = i; //记录下顶点索引，此时Y轴更小

else if (cP->y > P[maxmax].y)

maxmax = i; //记录下顶点索引，此时Y轴更大

}

if (xmin == xmax) { // 一种极端情况出现：X轴最小与最大数值相同，即所有数值等同

H[++top] = P[minmin]; //记录下此顶点

if (minmax != minmin) // 如果Y轴的数值不同

H[++top] = P[minmax]; //记录下此顶点

return top+1; // 返回顶点个数，这种特殊情况下是1或2个

}

Bin* B = new Bin[k+2]; // 初始化区间数据结构

B[0].min = minmin; B[0].max = minmax; // 设置第一个区间

B[k+1].min = maxmin; B[k+1].max = maxmax; // 设置最后一个区间

for (int b=1; b<=k; b++) {

B[b].min = B[b].max = -99; // 初始赋值

}

for (int b, i=0; i<n; i++) { //循环处理每个顶点

cP = &P[i];

if (cP->x == xmin || cP->x == xmax) // 如果是整个集合中的X轴最小或最大数值

continue; //继续下次循环

if (isLeft( P[minmin], P[maxmin], *cP) < 0) { // 当前顶点处于低线之下

b = (int)( k * (cP->x - xmin) / (xmax - xmin) ) + 1;//得Bin结构的序号

if (B[b].min == -99) // 这个Bin结构中还没有赋Y轴上的最低顶点

B[b].min = i; //记录索引

else if (cP->y < P[B[b].min].y) //若比已经记录的最低数值还低

B[b].min = i; // 新的最低顶点

continue;

}

if (isLeft( P[minmax], P[maxmax], *cP) > 0) { //当前顶点处于高线之上

b = (int)( k * (cP->x - xmin) / (xmax - xmin) ) + 1; //得Bin结构的序号

if (B[b].max == -99) // 这个Bin结构中还没有赋Y轴上的最高顶点

B[b].max = i; //记录索引

else if (cP->y > P[B[b].max].y) //若比已经记录的最高数值还高

B[b].max = i; //新的最高顶点

continue;

}

//和前面讲解的Andrew's Monotone Chain算法中一样，使用 “左转”方式来判断凸包条件是否成立，分别构成上下两个子集

for (int i=0; i <= k+1; ++i)//对每个区间循环处理

{

if (B[i].min == -99) // 如果区间中没有最低顶点记录的话，继续下次循环

continue;

cP = &P[ B[i].min ]; // 取出当前区间中的最低顶点

while (top > 0) // 当栈中至少有2个元素的时候，top > 0

{

// 看是否满足“左转”条件

if (isLeft( H[top-1], H[top], *cP) > 0)

break; // 此顶点是满足条件的新凸包顶点

else

top--; // 由于顶点破坏凸包条件，需要弹出栈顶元素，直到满足

}

H[++top] = *cP; // 将这个顶点压入栈

}

//下面，计算上半部分的凸包顶点集合

if (maxmax != maxmin) //如果X轴数值最大情况下Y轴有不同顶点存在

H[++top] = P[maxmax]; //将X轴数值与Y轴数值最大的顶点压入栈

bot = top; //记住准备增加元素到栈前已经存在的元素个数

for (int i=k; i >= 0; --i) //对每个区间循环处理

{

if (B[i].max == -99) //如果区间中没有最高顶点记录的话，继续下次循环

continue;

cP = &P[ B[i].max ]; //取出当前区间中的最高顶点

while (top > bot) // top还是比开始记住的bot大，表明栈中至少有2个元素

{

// 看是否满足“左转”条件

if (isLeft( H[top-1], H[top], *cP) > 0)

break; //此顶点是满足条件的新凸包顶点

else

top--; //由于顶点破坏凸包条件，需要弹出栈顶元素，直到满足

}

H[++top] = *cP; //将这个顶点压入栈

}

if (minmax != minmin) //如果X轴数值最小情况下Y轴有不同顶点存在

H[++top] = P[minmin]; //把这最后一个顶点压入栈

delete B; // 释放

return top+1; //返回输出的凸包数组中的顶点个数
}

介绍完平面上凸包各种求取方法后，讲解三维顶点集合凸包的方法。

过程：

3DConvexHull( int argc, char *argv[] )

{
ReadVertices(); //读取所有顶点

DoubleTriangle(); //构造初始三角形

ConstructHull(); //构建三维顶点集合的凸包

}

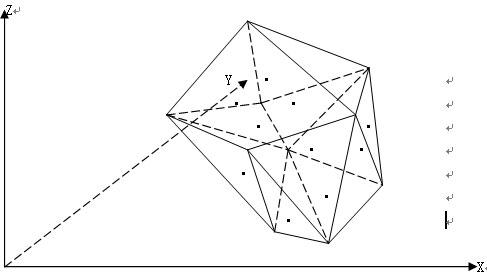
//首先找到3个不共线的顶点，以相反的顺序建成三角形的两个面。接着找到不在三角面上的第四个顶点。在三角面上以逆时针顺序存储顶点，建立到新顶点的3个面。

void DoubleTriangle( void )

{

tVertex v0, v1, v2, v3, t;

tFace f0, f1 = NULL;

tEdge e0, e1, e2, s;

int vol;

v0 = vertices;

while ( Collinear( v0, v0->next, v0->next->next ) )//比较连续存储的3个顶点

if ( ( v0 = v0->next ) == vertices ) //提取下一个顶点

printf("所有顶点共线");

v1 = v0->next; //找到不共线的顶点

v2 = v1->next; //找到不共线的顶点

v0->mark = PROCESSED; //标记顶点处理过

v1->mark = PROCESSED; //标记顶点处理过

v2->mark = PROCESSED; //标记顶点处理过

f0 = MakeFace( v0, v1, v2, f1 );

f1 = MakeFace( v2, v1, v0, f0 );//以相反的顶点顺序构建第二个面

f0->edge[0]->adjface[1] = f1;

f0->edge[1]->adjface[1] = f1;

f0->edge[2]->adjface[1] = f1; //指出面的邻接面

f1->edge[0]->adjface[1] = f0;

f1->edge[1]->adjface[1] = f0;

f1->edge[2]->adjface[1] = f0; //指出面的邻接面

//准备找到不在面上的第四个顶点来构建体

v3 = v2->next;

vol = VolumeSign( f0, v3 ); //通过计算体积来判断是否第四个顶点不在面上

while ( !vol ) { //当体积为0的话，继续循环

if ( ( v3 = v3->next ) == v0 )

printf("所有顶点是共面的");

vol = VolumeSign( f0, v3 );

}

vertices = v3; //记录V3为现在被增加的顶点

}

//每次考察一个顶点，如果构成凸包中新顶点，则新建面和边，如处在现阶段的凸包之内，则不作其他处理；

void ConstructHull( void )

{

tVertex v, vnext;

int vol;

bool changed;

v = vertices;

do {

vnext = v->next; //取下一个顶点来处理

if ( !v->mark ) { //如果此顶点的标记为“还从未处理过”

v->mark = PROCESSED;//将此顶点标记为“已经被处理过”

changed = AddOne( v );//将新顶点加入，处在现凸包内，或构成新凸包的一个顶点

CleanUp( &vnext );

}

v = vnext;

} while ( v != vertices );

}

通过体积来计算此顶点与其他面的关系，若构成的体都为凹，则不予考虑。否则，可说此顶点位于某些面之外。若从此顶点能观察到某边的两个邻接面，则此边将被删除。若从此顶点只能观察到一个面，则将创建新面。

bool AddOne( tVertex p )

{

tFace f;

tEdge e, temp;

int vol;

bool vis = FALSE;

f = faces;

do {

vol = VolumeSign( f, p ); //计算每个面和新增加的顶点构成的锥体的体积

if ( vol < 0 ) {

f->visible = VISIBLE; //此面被标记为可见

vis = TRUE; //标识顶点已处于面之外

}

f = f->next; //取得下一个面

} while ( f != faces ); //对所有面循环处理

if ( !vis ) { //没有一个面可见，则顶点位于体内，不将作为凸包顶点

p->onhull = !ONHULL; //顶点作标记

return FALSE;

}

e = edges;

do {

temp = e->next; //取下一条边

if ( e->adjface[0]->visible && e->adjface[1]->visible )

e->delete = REMOVED;//如果这条边的两个邻接面都可见，则标记为删除此条边

else if ( e->adjface[0]->visible || e->adjface[1]->visible )

e->newface = MakeConeFace( e, p ); //构建新面

e = temp;

} while ( e != edges ); //所有边循环处理

return TRUE;

}

//计算体积，此结果的正负可判断顶点与面的“可见”关系。

int VolumeSign( tFace f, tVertex p )

{

double vol;

int voli;

double ax, ay, az, bx, by, bz, cx, cy, cz;

ax = f->vertex[0]->v[X] - p->v[X];

ay = f->vertex[0]->v[Y] - p->v[Y];

az = f->vertex[0]->v[Z] - p->v[Z]; //顶点坐标相减构成向量

bx = f->vertex[1]->v[X] - p->v[X];

by = f->vertex[1]->v[Y] - p->v[Y];

bz = f->vertex[1]->v[Z] - p->v[Z];

cx = f->vertex[2]->v[X] - p->v[X];

cy = f->vertex[2]->v[Y] - p->v[Y];

cz = f->vertex[2]->v[Z] - p->v[Z];

vol = ax * (by*cz - bz*cy)

+ ay * (bz*cx - bx*cz)

+ az * (bx*cy - by*cx);

//体积计算是通过法向量与一条边向量的点乘，因为点乘结果表示两个模与向量夹角的余弦，其中法向量的模是三角面上两条边的模乘上夹角的正弦，即为面积。而剩下的那个模乘上夹角的余弦，即为高。

return vol;

}

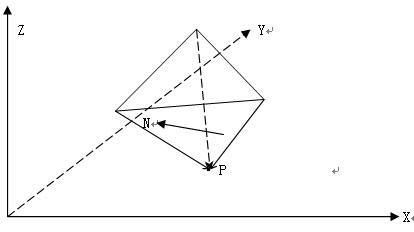
当一条边的一个邻接面对新加入的顶点是“可见”的时候，构建一个新面和两条新边

tFace MakeConeFace( tEdge e, tVertex p )

{

tEdge new_edge[2];

tFace new_face;

int i, j;

//准备构建两条新边

for ( i=0; i < 2; ++i )

//如果新边已经被创建过，直接拷贝过来即可

if ( !( new_edge[i] = e->endpts[i]->duplicate) ) {

//如果新边没有被创建过，则构建

new_edge[i] = MakeNullEdge();

new_edge[i]->endpts[0] = e->endpts[i];

new_edge[i]->endpts[1] = p;

e->endpts[i]->duplicate = new_edge[i];// 顶点标记这条新边

}

//创建新的面

new_face = MakeNullFace();

new_face->edge[0] = e; //构成面的原来那条边

new_face->edge[1] = new_edge[0];//构成面的第一条新边

new_face->edge[2] = new_edge[1]; //构成面的第二条新边

MakeCcw( new_face, e, p ); //以逆时针方向建立面上的顶点顺序

//将新建立的边和面联系起来

for ( i=0; i < 2; ++i )

for ( j=0; j < 2; ++j )

if ( !new_edge[i]->adjface[j] ) {

new_edge[i]->adjface[j] = new_face;

break; //新边和新面一旦联系,就跳出循环

}

return new_face;//处理结束,返回新建立的面

}

当折线的端点过于密集，以至于显示时堆积在一起时，有必要简化折线，以提高后续凸包或相交运算的处理效率与显示清晰度。关键问题是如何简化复杂折线，能够保持其特征，不至于失真。

第一步通过设置顶点之间的距离阈值来减少冗余顶点。

第二步，采用Douglas-Peucker (DP)算法简化折线，其在计算机图形学与地理信息系统领域被广泛应用。

其思想是顶点到某条边的距离过于接近的话，将被舍弃，保留距离大于阈值的顶点。初始化时，首先连接第一个和最后一个顶点构建第一条边，找到剩余顶点中距离这条线段最远的顶点，然后分别连接第一和最后一个顶点到此最远的顶点，构成两条线段，继续寻找剩余顶点中分别到这两条线段距离最远的顶点，依此类推，直到顶点到边的距离小于设置的阈值停止处理，那么找到的这些顶点构成了简化折线。

// 折线的简化程序，包含上述两步骤

// 输入：阈值 tol，折线的顶点数组 V[]，顶点的个数 n；

// 输出: 经过简化后的顶点数组 sV[]；

// 返回: 简化后的顶点数组中的顶点数量 m；

int CDEMAlgorithm::poly_simplify( double tol, Point* V, int n, Point* sV )

{

int i, k, m, pv; //准备用做计数器

double tol2 = tol * tol; //阈值的平方

Point* vt = new Point[n]; // 输入的顶点数组

int* mk = new int[n]; //给标记数组初始化

for(i=0;i<n;i++)

{

mk[i] = 0; // 初始化

}

//第一步：通过顶点之间的距离判断，是否保留某些顶点

vt[0] = V[0];

for (i=k=1, pv=0; i<n; i++) { //对输入的每个顶点循环处理

if (d2(V[i], V[pv]) < tol2) //顶点之间的距离小于阈值，直接跳到下个顶点进行处理

continue;

vt[k++] = V[i]; //顶点之间的距离大于阈值，记录此顶点

pv = i; //记录此顶点的索引号

}

if (pv < n-1)

vt[k++] = V[n-1]; // 将最后一个顶点记录下来

//第二步：采用 Douglas-Peucker算法进行简化

mk[0] = mk[k-1] = 1; // 给第一个和最后一个顶点标记为1

simplifyDP( tol, vt, 0, k-1, mk );

// copy marked vertices to the output simplified polyline

for (i=m=0; i<k; i++) {

if (mk[i]) //如果标记为1的话

sV[m++] = vt[i]; //将顶点赋值给最后输出的结果数组

}

delete vt; //删除临时顶点数组

delete mk; //删除标记数组

return m; // m vertices in simplified polyline

}

// Douglas-Peucker (DP)算法

// 输入: 阈值tol，顶点数组v[]，j,k分别指示顶点数组中的第一和尾部顶点，在第一次运行此程序片段时，表示连接最初和最后的顶点构成线段，在后面的递归调用中，表示连接到最远顶点的子线段；

// 输出: 简化后的顶点数组 mk[]；

void CDEMAlgorithm::simplifyDP( double tol, Point* v, int j, int k, int* mk )

{

if (k <= j+1) // 两顶点挨在一起，没必要简化

return;

int maxi = j; // 准备记录距离线段的最远顶点的索引

double maxd2 = 0; // 准备记录最远距离的平方

double tol2 = tol * tol; // 设置的阈值的平方

Segment S = {v[j], v[k]}; // 构建顶点v[j] 和 v[k]之间的线段

Vector u = S.P1 - S.P0; //矢量

double cu = Dot(u,u); // 线段长度的平方

// 采用前面讲解的顶点到线段的距离求法，计算每个顶点到线段S的距离

Vector w;

Point Pb;

double b, cw, dv2;

for (int i=j+1; i<k; i++)

{

w = v[i] - S.P0;

cw = Dot(w,u);

if ( cw <= 0 )

dv2 = d2(v[i], S.P0);

else if ( cu <= cw )

dv2 = d2(v[i], S.P1);

else {

b = cw / cu;

Pb = S.P0 + b * u;

dv2 = d2(v[i], Pb);

}

if (dv2 <= maxd2)

continue;

// v[i]是符合要求的最远顶点

maxi = i;

maxd2 = dv2;

}

if (maxd2 > tol2) // 如果最远顶点到线段S的距离大于阈值

{

mk[maxi] = 1; //记录maxi这个索引，此顶点将被最后输出

//递归调用此程序

simplifyDP( tol, v, j, maxi, mk ); // 第一条子线段

simplifyDP( tol, v, maxi, k, mk ); // 第二条子线段

}

return;

}