二叉查找树（binary search tree）的实现算法分析

此文为《data abstraction and problem solving with c++》的读书笔记 。这里有个图书管理系统模拟的应用实例

       树中的每一个节点包含特定人员的数据。人名是查找关键字，是可在图中看到的唯一的数据项。下面的c++语句描述了树节点中的数据：

#include<string>using namespace std;typedef string keyType;class KeyItem{public:KeyItem();KeyItem(const KeyType &keyValue):searchKey(keyValue){}KeyType getKey()const{return searchKey;}private:KeyItem searchKey;};class Person :public KeyItem{public:Person();Person(const string &name,const string &id,const string &phone):KeyItem(name),idNum(id) ,phoneNumber(phone){}private:string idNum;string phoneNumber;};

       因为二叉查找树的本质上是递归的，所以很自然为树的操作设计递归算法。假设要在图1的二叉树中查找Ellen的记录。Jane在树的根节点中，所以若树中存在Ellen的记录，则必然在Jane的左子树中，因为按字母顺序，查找关键字Ellen在查找关键字Jane之前。有递归的定义知，Jane的左子树也是二叉树，因此可用完全相同的策略，在子树中查找ELlen。Bob是这个二叉查找树的根，因为关键字Ellen大于关键字Bob，所以Ellen的记录必然在Bob的右子树中。Bob的右子树也是二叉查找树，而Ellen正好在该树的叶节点中。这样就找到了Ellen的记录。

                                      

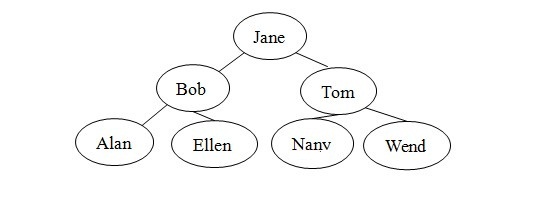
                                                                     图1：二叉查找树
       下面的伪码总结了查找策略：

search(in binTree:BinarySearchTree,in searchKey:KeyType)//Search the binary search tree for the item //whose search key is searchKey{if(binTree is emtpy)the desired record is not found;else if(searchKey == search key of root's item)the desired record is found;else if(searchKey< search keyof root's item)search(left subtree of binTree,searchKey);elsesearch(right subtree of binTree ,searchKey);}

       后面将会看到，search算法是二叉查找树的插入、删除和检索操作的基础。
很多不同结构的二叉查找树可以包含人名Alan、Bob、Ellen、Jane、Nancy、Tom和Wendy。例如，除图1的树外，图2的每棵树都是人名的有效二叉查找树。虽然形状各不相同，但树的形状并不影响search算法的有效性。算法只要求树是二叉查找树。
对于search方法而言，一些树比另一些树的效率会更高。例如，在图2-c中，search算法在检查每个节点之后才找到Wendy，实际上，这个二叉查找树的结构与有序线性连接表相同，没有效率优势。而对于图1中的满二叉树，search算法只检查包含人名Jane、Tom和Wendy的节点。这些人名与图3中有序数组的折半查找将检查的人名相同。后面将进一步介绍二叉查找树的形状如何影响search的效率，以及插入和删除操作如何影响树的形状。

                                                           

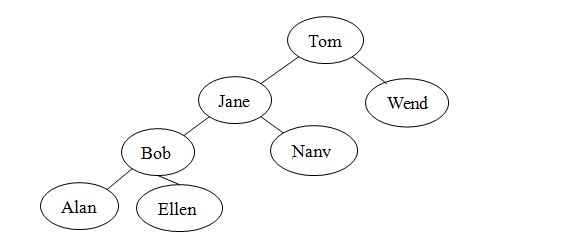
                                                                                  （a）

                                                     

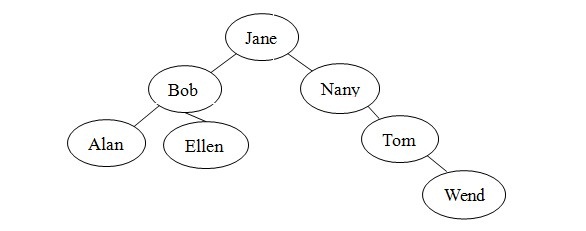
                                                                                   （b）

                                                         

                                                                                   （c）    
                                                                图2：与图1包含相同数据的二叉查找树

                                  
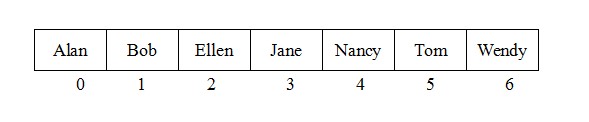
                                                                              有序的人名数组
       下面介绍的插入、删除、检索和遍历算法假设采用前面讨论的二叉树的基于指针的实现。稍作改动，即可将这些基本算法用于二叉树的其他实现。还假设节点项具有唯一查找关键字。
 Insert
       假设要将Frank的记录插入图1的二叉查找树中。第一步查找包含关键字Frank的项。search算法首先查找根为Jane的树，然后查找根为Bob的树，在查找根为Ellen的树。之后，查找以Ellen的右左孩子为根的树。如图3所示，因为树空，所以search算法到达基例，终止，并显示消息：不存在Frank。search在Ellen的右子树查找Frank意为着什么？首先，若Frank是ELlen的右孩子，则search将在那里找到Frank。
       由这些观察可知，最好将Frank作为Ellen的右孩子插入。因为Ellen没有右孩子，所以插入很简单，只需要是Ellen的RightChild指针指向包含Frank的节点。更重要的是，Frank属于这个位置--search将在此处查找到Frank。更明确地讲，将Frank作为Ellen的右孩子插入将保持二叉查找树的属性。因为在查找Frank时，search将遵循到达Ellen的右孩子的路径，故可以确保：Frank与树中上部人名的关系正确。

                                    
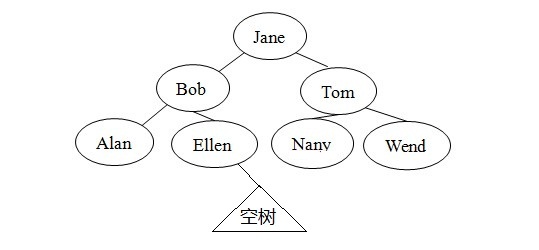
                                                               图3：search 算法在空子树终止
      使用search来确定在树中哪个位置插入新人名称简化了插入操作。无论将哪个新项插入树中，search总在空树处终止，这样，search总是将记录作为新叶子插入。因为添加叶子只需要改双亲中的适当指针，所以插入需要的工作实际上与对应的查找是相同的。
      下面的高级伪码描述了这个插入过程：

 insertItem(in treePtr:treeNodePtr, in newitem :TreeItemType) //inserts newitem into the binary tree of //which treePtr is the root{Let parentNode be the parent of the empty subtreeat which search terminates when it seeksnewitem's search keyif(Search terminated at parentNode's lefat subtree)set leftChildPtr of parentNode to point to newitemelseset rightChildPtr of ParentNode to point to newitem}

       必须将节点parentNode的适当指针leftChildPtr 或rightChildPtr 设置为指向新的节点。后面将看到，若将treePtr传递为引用参数，则search算法的递归特性提供了设置指针的巧妙方法。于是将insertItem方法完善为：

//inserts newitem into the binary search tree of//which treePtr is the root{if(treePtr is NULL){Create a new node and let treePtr point to itcopy newitem into new node's data portionset the pointers in the new node to NULL}else if(newitem.getKey()<treePtr->item.getKey())insertItem(treePtr->leftChildPtr,newitem);elseinsertItem(treePtr->rightChildPtr,newitem);}

      该递归算法如何将leftChildPtr或rightChildPtr设置为指向新的节点呢？这与第四章介绍的有序链表的递归插入函数非常相似。若插入前树为空，则树的根的外部指针将为NULL，而且函数不会做递归调用。因为treePtr是引用参数，在它指向新节点时，实参，即树根的外部指针，也将指向新节点。图4-a显示在空树中插入（试想一下该递归的参数传递在C语言中是怎样实现的）。
                           

                                                （a）                                                                     （b）

                                             

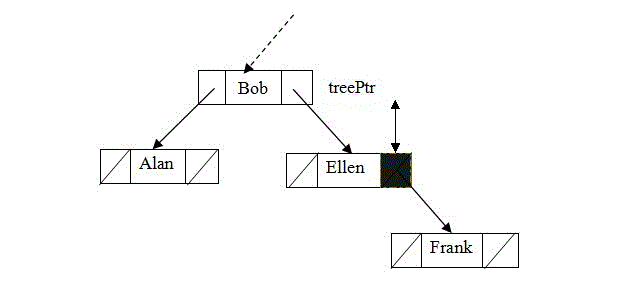
                                                                                  （c）

                                        图4 （a）在空树中插入；（b）查找在叶子处终止；（c）在叶子处插入

         insertItem的一般情况与空树的特例类似。当形参treePtr变成NULL时，对应的实参是空子树双亲中的leftChildPtr 或rightChildPtr指针，换言之，这个指针的值为NULL。通过一个递归调用，将该指针传给insertItem函数：
                                insertItem(treePtr->leftChildPtr,newitem);
                               或
                                insertItem(treePtr->rightChildPtr,newitem);
       因此,当treePtr指向新节点时，形参，即双亲中的对应指针，就指向新的节点。图4中的b部分和c部分显示插入的一般情况。
可用insertItem构建二叉查找树。例如，从空树开始，若按次序插入Jane Bob Alan Ellen Tom Nancy 和Wendy，将得到如图1所示的二叉查找树。有趣的是，Jane Bob Alan Ellen Tom Nancy和Wendy正好是图1中树的先序遍历。也就是说，若取出二叉查找树的先序遍历的输出，并使用insertItem 构建二叉查找树，将得到一颗重复树。这没什么可以惊讶的，因为ADT二叉树的副本构造函数就是使用先序遍历复制树。
若按不同顺序插入前面的人名，则将得到一颗不同的二叉查找树。例如，按字母表顺序插入前面的姓名，将得到图2-c的二叉查找树。

delete
        删除比插入要复杂些。首先用search算法来定位包含指定查找关键字的项，若找到，则必须从树中删除此项。算法的初始版本如下：

deleteItem(inout treePtr :TreeNodePtr,in searchKey :KeyType)throw TreeException//deletes from the binary search tree to which treePtr//points the item whose search key equals searchKey.if No//such item exist ,the operation fails and throws TreeException{Locate (by using search algorithm) the item iwhose search key equals searchKeyif(item is Found)remove item i from the treeelsethrow a tree exception}

       关键任务在于：
                                  Remove item i from the tree
       假设deleteItem在特殊节点N中找到项目i，分三种情况考虑：
           （1）N是叶子
           （2）N只有一个孩子
           （3）N有两个孩子
       第一种情况最容易处理。要删除包含元素i的叶子，只需要将其双亲的指针设置为NULL。
       第二种情况比较更复杂；若N有一个孩子，则有两种可能性：
              * N只有一个左孩子
              * N中有一个右孩子
       这两种可能性是对称的，因此，演示左孩子的解决方案就够了。在图5-a中，L是N的左孩子，而P是N的双亲。N可以是P的左孩子，也可以是P的右孩子。若树中删除节点N，L将没有双亲，P将去掉一个孩子。设使L替代N，作为P的一个孩子，如图5-b所示。这种方法保持了二叉查找树的属性吗？
       例如，若N是P的左孩子，则以N为根的子树的查找关键字都小于P中的查找关键字。同样，以L为根的子树的所有查找关键字都小于P中的查找关键字。所以，再删除N，而且P收养了L后，P的左子树的所有查找关键字仍小于P中的查找关键字。因此，该删除策略保持了二叉查找树的属性。若N是P的右孩子，则方式类似。总之，在两种情况下，都保持了二叉查找树的属性。

            图5：（a）N只有一个左孩子，N可以是P的左孩子也可以是P的右孩子；        （b）删除节点N后
       若要删除的项处在包含两个孩子的节点N中，则处理更困难，是三种可能中的最复杂的情况。
如图6所示。由上可知，当N只有一个孩子时，该孩子将替代N。而当N有两个孩子的情况下，不可能是两个孩子都替换N，N的双亲的空间有限，只能由N的一个孩子作为N的替代。很显然，需要一种不同的策略。

                                                     
                                                                       图6 ：N有两个孩子
      实际上，根本不必删除节点N。可找到另一个更易删除的节点，不删除N，而删除该节点。该策略似乎难以置信。但是，程序员编写下列语句
                                nameTree.searchTreeDelete(searchKey);
       是期望从ADT二叉查找树中删除关键字等于searchKey的项。不过，编程者只希望删除该项，因为程序和ADT实现之间的墙，所以他们无权删除树中的节点。...//?
       考虑另一种策略（怎样考虑到的？？）。要从二叉查找树中删除包含两个孩子的节点N中的项，可采用下列步骤：
             （1）在树中定位另一个节点M，M比N更容易删除。
             （2）将M中的项复制到N，从而有效地从树中删除N的原始项。
             （3）从树中删除节点M。
       哪类节点M比节点N更容易删除？前面介绍了如何删除没有孩子或只含有一个孩子的节点，故可将此类节点用作M。但用小心，并不能随意在选择一个节点，将其数据复制到N，原因是必须将树的状态保持为二叉查找树。例如，在图7的树中，若将M的数据复制到N，则结果将不再是一个二叉查找树。

                                                    
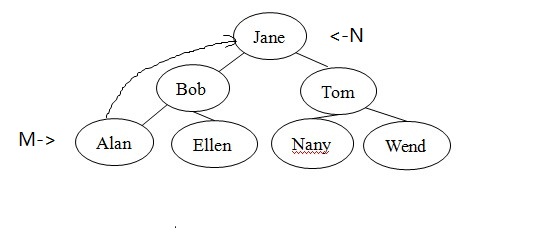
                                                                        图7：并非任何节点都可用
      究竟将哪个数据项复制到节点N，可以将树的状态保持为二叉查找树？N的左子树的所有查找关键字都小于N中的查找关键字，而N的右子树的所有查找关键字都大于N中的查找关键字。在用查找关键字y替换节点N中的查找关键字x时，必须保持这个属性。y值有两种可能性：按查找关键字的顺序，y可能紧接在x之前，也可以紧接在x之后。如果y紧接在x之后，则N的左子树的所有查找关键字都小于y，应为他们都小于x,如图8所示。而N的右子树的所有查找关键字都大于等于y，因为它们大于x，而且根据假设，该树不存在介于x和y之间的查找关键字。若按查找关键字的顺序，y紧接在x之前，则y大于等于N的左子树的所有查找关键字，而小于N的右子树的所有查找关键字。

                                                
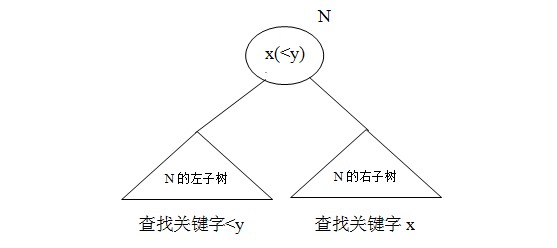
                                                                     图8：可用y代替查找关键字x

       因此，可将查找关键字紧接在N的查找关键字之后的项复制到N，也可以将查找关键字紧接在N的查找关键字之前的项复制到N 。假设要使用查找关键字y 紧接在N的查找关键字之后的节点。这个查找关键字称为x的中序后继（inorder successor）。如何定位该节点？因为N有两个孩子，所以查找关键字的中序后继是N的右子树的最左侧节点。换言之，要查找包含y的节点，可以跟踪指向N的右孩子R的rightChild指针（这一定存在，因为N有两个孩子）。然后沿以R为根的树向下，采用各个节点的左分枝，直到遇到没有左孩子的节点M为止。将节点M的项复制到N，M没有左孩子，故可用两种简单情况之一从树中删除M。如图9所示。

                                              
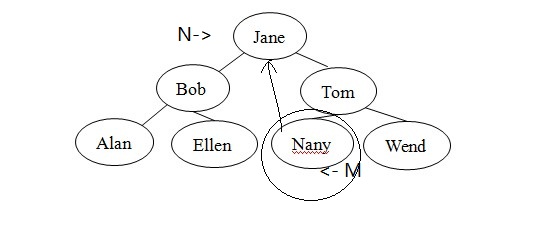
                                   图9：M的查找关键字是N的查找关键字的中序后继，将M的数据项复制到N
      下面是更详细的删除算法的高级描述：

deleteItem(inout treePtr:TreeNodePtr,in searchKey :TreeItemType)//deletes from the binary search tree to which//treePtr points the item whose search Key equals //seachKey . if no such item exists ,the operation//fails and throws treeException{Locate (by using the search algorithm) theitem whose search key equal seachKeyit occurs in node iif(item is found node N)deleteNodeItem(N)elsethrow a tree exception}deleteNodeItem(inout N:treeNode)//deletes the item in a node N of a binary//search tree.{if(N is a leaf)remove N from the treeelse if(N has only one child C){if(N was a left child of its parent P)Make C the left child of PelseMake C the right child of P}//personal :something misunderstanding hereelse //treeNode has the two childen{Find M ,the node that contains N's Inorder successorcopy the item from node M into node NRemove M from the tree by using the previoustechnique for a leaf or a node with one child}}

       在下面的完善代码中，采用了search的算法，并将其直接插入到deleteItem。另外，函数deleteNodeItem 使用ProcessLeftMost函数查找节点M中的项。即节点N的中序后继。函数processLeftMost返回M的项，此后，从树中删除M。然后用返回的项替换节点Ｎ中的项，从而将其从二叉查找树中删除。

deleteItem(inout treePtr:TreeNodePtr,in searchKey:KeyType)throw treeException//deletes from the binary search tree to which//treePtr points the item whose search key equals searchKey ,//if no such item exists,the operation //fails and throws treeException{if(treePtr==NULL)throw TreeException//item not foundelse if(searchKey=treePtr->item.getKey())deleteNodeItem(treePtr);else if(searchKey<treePtr->item.getKey())deleteItem(treePtr->leftChildPtr,searchKey);else deleteItem(treePtr->rightChildPtr,searchKey);}deleteNodeItem(inout treePtr:TreeNodePtr)//deletes the item in the node N to which nodePtr points{if(N is a leaf){delete nodePtr;nodePtr=NULL;}else if(N has only one child C){//C replace N as the child of N's parentdelPtr= nodePtr;if(C is the left child of N)nodePtr=nodePtr->leftchildPtr;else node Ptr=nodePtr->rightChildPtr;delete delPtr;}else //N has two children {    //find the inorder successor of the search key in //N :it is in the leftmost node of the//subtree rooted at N's right childProcessLeftMost(nodePtr->rightChildPtr,replaceItem);put replaceitem in node N;}}ProcessLeftMost(inout nodePtr:treeNodePtr,out treeItem :TreeItemType)//retrieve into treeitem the item in the leftmost//descendant of the node to which nodePtr points//delete the node that contains this item {if(nodePtr->leftChildPtr==NULL){//this is the node you want ,it has no left//child ,but it might have a right subtreetreeItem =nodePtr->item;delPtr=nodePtr;//the actual argument corresponding to nodePtr is a//child pointer of nodePtr's parent;thus the following//"moves up" nodePtr's right subtreenodePtr = nodePtr->rightChildPtr;delete delPtr;}elseprocessLeftMost(nodePtr->leftChildPtr,treeitem);}

       与insertItem函数一样，与treePtr对应的实参要么是N的双亲的指针之一，如图10所示，要么是根的外部指针（此时，N是原始树的根）。无论哪种情况，treePtr都指向N。这样若通过实参treePtr调用deleteNodeItem函数更改treePtr，则将更改Nde双亲的指针。若Ｎ有两个孩子，deleteNodeItem将调用递归函数processLeftMost ,使用相同的策略，删除包含待删除项的节点的中序后继。

                                              
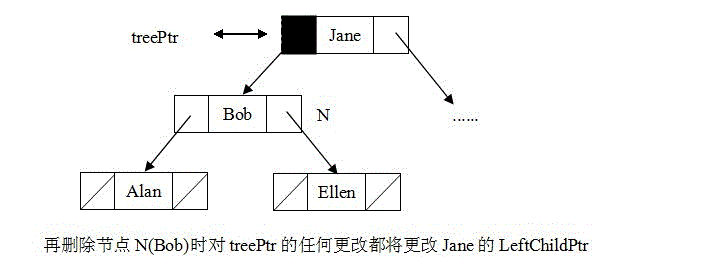
                                                               图10：节点N的递归删除
retrieve

       通过完善search算法，可实现检索操作。search算法的代码如下：

search(in bst :BinarySearchTree ,in searchKey :keyType)//searchs teh binary tree bst for the item//whose search key is searchKey{if(bst is empty)the desired record is not foundelse if(searchKey==search key of bst's root item)the desired record is foundelse if(searchKey<search key of bst's root item)search(left subtree of bst,searchKey)elsesearch(right subtree of bst,searchKey)}

       如果存在需要的查找关键字，则检索操作必须返回包含该关键字的项。否则，必须抛出异常TreeException 所以，检索的算法如下：

retrieveItem(in treePtr:treeNodePtr,in searchKey :keytype,out treeItem :treeItemType)throw TreeException//returns into treeitem the item whose search key equals searchKey //from the binary search tree//to which treePtr points .the operation //throws treeException if no such item exist.{if(treePtr==NULL)throw a tree exception indicating item not foundelse if(searchKey==treePtr->item.getKey())//item is in the root of some subtreetreeItem =treePtr->item;else if(searchKey<treePtr->item.getKey())retrieveItem(treePtr->leftChildPtr,searchKey);else retrieveItem(treePtr->rightChildPtr,searchKey);}

traverse 
       二叉查找树与二叉树的遍历相同，但要认识到，二叉查找树的中序遍历将按有序的查找关键字的顺序访问树的节点。在证明此陈述前，先回顾一下中序遍历算法：

inorder(in bst:BinarySearchTree)//traverses the binary tree bst in inorder{if(bst is not empty){inorder(bst->leftChildPtr);visit the root of Tinorder(bst->rightChildPtr);}}

       定理二：叉查找树T的中序遍历将按有序的查找关键字的顺序访问节点。
       证明 此证明在T的高度h上归纳。
       基例：h=0。当树空时，算法不访问任何节点。对于树中人名为零的情况，这当然是有序的。
       归纳假设：假设对所有k，0<k<h，这定理成。换言之，对于所有k(0<k<h),中序遍历按有序的查找关键字顺序访问节点。
       归纳结论：必须说明，对于k=h>0，该定理成立。T的形式为：

                                         
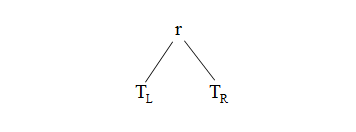
       因为T是二叉查找树，所以左子树TL中的所有查找关键字都小于根r的查找关键字，而右子树TR中的所有关键字都大于根r的查找关键字。inorder算法将访问TL中的所有节点，然后访问r，在访问TR中的所有节点。所以，唯一考虑的是inorder按正确顺序访问TL和TR子树的各个节点。但是因为T是高为h的二叉查找树，所以两棵树都是高度小于h的二叉查找树。按照归纳假设，inorder将按正确的有序关键字的顺序访问TL和TR子树的节点。证毕。
       由此定理知：inorder在访问节点后立即访问节点的中序后继。