高效地安排见面会扩展问题

        扩展问题一：某一天，在微软亚洲研究院有N个面试要进行，它们的时间分别为(B[i], E[i])（B[i]为面试开始时间，E[i]为面试结束时间）。假设一个面试者一天只参加一个面试。为了给面试者提供一个安静便于发挥的环境，我们希望将这N个面试安排在若干个面试点。不同的面试在同一个时间不能被安排在同一个面试点。如果你是微软亚洲研究院的HR，现在给定这N个面试的时间之后，你能计算出至少需要多少个面试点吗？请给出一个可行的方案[1]。

        这个问题可以用图模型求解。每场面试是一个顶点，如果两场面试时间上有重叠，就用一个边把它们连起来。这样，这个问题就转换成了一个图的最少着色问题。对于这个问题，是否在多项式时间复杂度内求出解呢[1]？《编程之美》的作者给出了一种采用贪心策略的算法，但是后面算法思路解释不是特别好懂，因此当时看的时候也没有仔细去琢磨，只是标记了一下自己觉得模糊地地方。昨天，在看完《算法导论》贪心算法一章后想起以前看过的这道题，就重新再仔细看了一遍。虽然这一次看懂了，但是仍觉得书上所说的思路条理不是很清晰。于是，我想是否可以从另外的思路来理解这种问题的解法。

        对于这个问题，要使面试的地点最少，就必须尽可能的把面试时间互相不重叠的面试安排在同一个面试点。

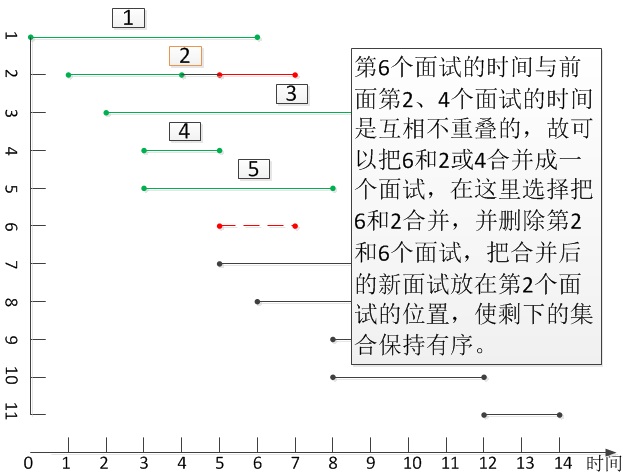
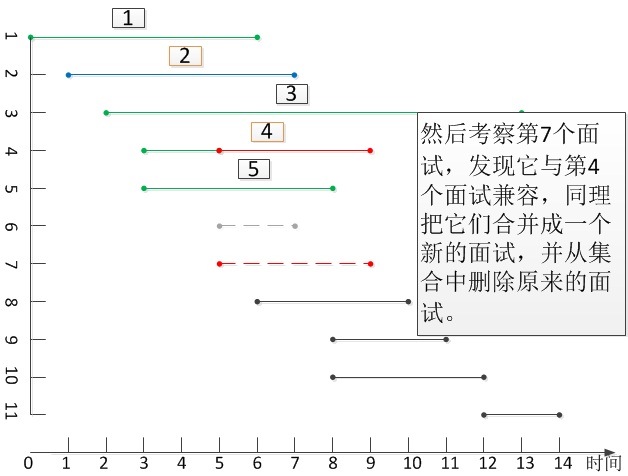
        思路1：一个含有N个面试的面试集合S = {(B[i], E[i]) | 0 <= i <= N}，其中的元素已经按面试的开始时间递增顺序排序，开始时间相同的面试则按其结束时间的递增顺序排序。对于面试集合S中一个面试I(B[j], E[j])，若在开始时间比I(B[j], E[j])早的所有面试中，存在一个（如有多个则任选一个即可）面试I(B[i], E[i])与其兼容（时间不重叠）。已知集合S中所有面试是按其开始时间的递增顺序排列的，则必定有B[i] <= B[j]，又这两个面试时间互相不重叠，则必定有E[i] < B[j]，因此必定有B[i] < E[i] < B[j] < E[i]。由于这两个面试可以在同一面试点先后紧挨着进行，因此可以把它们看成是一个面试，合并后的新面试为I(B[i], E[j])。然后，在集合S中把原来的两个面试删除，并把合并后的新面试I(B[i], E[j])放在原来面试I(B[i], E[i])的位置，使集合S中剩下的面试仍然保持有序。接着考察与面试I(B[j], E[j])相邻的下一个面试，按上述思路进行合并，直到考察到最后一个面试为止。此时，集合S中不再存在互相兼容的面试。因此，集合S中剩下的面试个数，即是N个面试所需的最少面试点的个数。

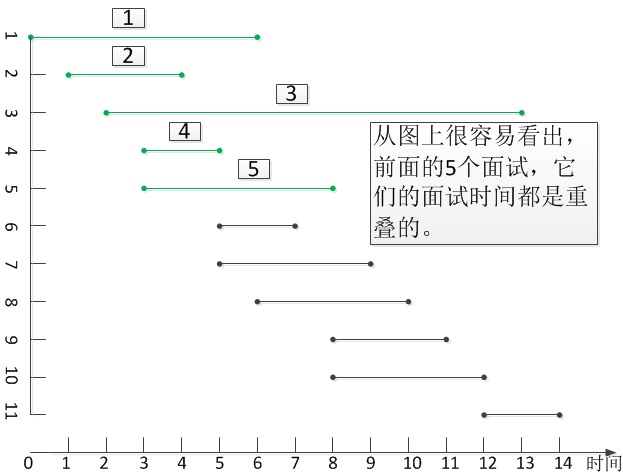
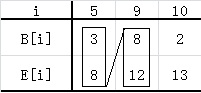
        上面的思路单纯看文字，其实也很不好理解，但是用图表达出来则感觉要条理清晰得多。例如，有下面面试集合：

把集合中所有面试按开始时间递增的顺序画在时间轴上，按顺序考察每一个面试是否可以和其前面的面试合并。具体步骤如下：

 

       

        思路2：对于上述面试集合S，利用贪心算法求出其最大相互兼容面试集合M（面试时间两两不重叠，可以在同一个面试点进行），并从原始集合S中删除M；然后对于剩下的集合S-M，利用贪心算法求其最大相互兼容面试集合Q，并从S-M中删除之；然后再求剩下集合中的最大相互兼容面试集合，直到剩下的集合为空集为止。统计最大相互兼容面试集合的个数，即是面试集合S所需的最少面试点个数。

        寻找活动集合S的最大相互兼容集合的方法[2]，在《算法导论》贪心算法一章中有详细的讲解。解决此问题的具体步骤可总结为：

        1）把面试集合S中的元素按其结束时间的递增顺序排列；

        2）求其最大相互兼容面试集合M，并从原始集合S中删除之；

        3）求集合S-M的最大相互兼容面试集合Q，并从集合S-M中删除之。重复此过程直到原始面试集合S中为空集为止；

        4）统计求出的最大相互兼容面试集合的个数，即是面试集合S所需的最少面试点个数。

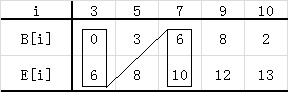
        以上面的面试集合S为例，上述步骤用图像表示如下：每个图中用矩形框起来的面试为所属集合的最大相互兼容集合，一共有5个，即至少需要5个面试点。

参考资料：

[1] 编程之美小组：《编程之美—微软面试心得》，2012， 57-61

[2] Thomas H. Cormen等：《算法导论（第二版）》，2012，222-226