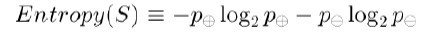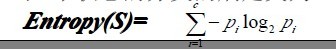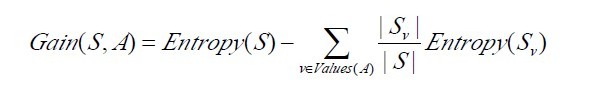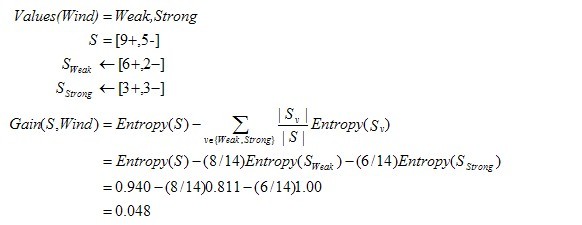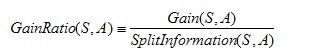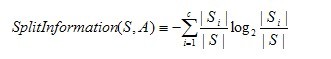从决策树学习 谈到贝叶斯分类算法

http://blog.csdn.net/v_july_v/article/details/7577684

        从决策树学习 谈到贝叶斯分类算法

引言

    最近在面试中，除了基础 & 项目之外，经常被问到或被要求介绍和描述下自己所知道的几种分类或聚类算法，而我向来恨对一个东西只知其皮毛而不得深入，故写一个有关聚类 & 分类算法的系列文章以作为自己备试之用(尽管貌似已无多大必要，但还是觉得应该写下以备将来常常回顾)。行文杂乱，但侥幸若能对读者也起到一定帮助，则幸甚至哉。

    本分类 & 聚类算法系列借鉴和参考了两本书，一本是Tom M.Mitchhell所著的机器学习，一本是数据挖掘导论，这两本书皆分别是机器学习 & 数据挖掘领域的开山 or 杠鼎之作，读者有继续深入下去的兴趣的话，不妨在阅读本文之后，课后细细研读这两本书。除此之外，还参考了网上不少牛人的作品(文末会注明参考链接)，在此，皆一一表示感谢。

    本分类 & 聚类算法系列暂称之为Top 10 Algorithms in Data Mining，其中，各篇分别有以下具体内容：

1. 开篇：决策树学习，与贝叶斯分类算法；
2. 第二篇：支持向量机SVM(support vector machine)，与神经网络ANN；
3. 第三篇：待定...

    说白了，一年多以前，我在本blog内写过一篇文章，叫做：数据挖掘领域十大经典算法初探(说实话，最初有个出版社的朋友便是因此文找到的我，尽管即便现在看来，我离出书日期仍是遥遥无期)。现在，我抽取其中几个最值得一写的几个算法每一个都写一遍，以期对其有个大致通透的了解。

    OK，全系列任何一篇文章若有任何错误，漏洞，或不妥之处，还请读者们一定要随时不吝赐教 & 指正，谢谢各位。

第一部分、决策树学习

1.1、什么是决策树

    咱们直接切入正题。所谓决策树，顾名思义，是一种树，一种依托于策略抉择而建立起来的树。

    机器学习中，决策树是一个预测模型；他代表的是对象属性与对象值之间的一种映射关系。树中每个节点表示某个对象，而每个分叉路径则代表的某个可能的属性值，而每个叶结点则对应从根节点到该叶节点所经历的路径所表示的对象的值。决策树仅有单一输出，若欲有复数输出，可以建立独立的决策树以处理不同输出。
    从数据产生决策树的机器学习技术叫做决策树学习, 通俗点说就是决策树。

    来理论的太过抽象，下面举两个浅显易懂的例子：

第一个例子

    套用俗语，决策树分类的思想类似于找对象。现想象一个女孩的母亲要给这个女孩介绍男朋友，于是有了下面的对话：

      女儿：多大年纪了？
      母亲：26。
      女儿：长的帅不帅？
      母亲：挺帅的。
      女儿：收入高不？
      母亲：不算很高，中等情况。
      女儿：是公务员不？
      母亲：是，在税务局上班呢。
      女儿：那好，我去见见。

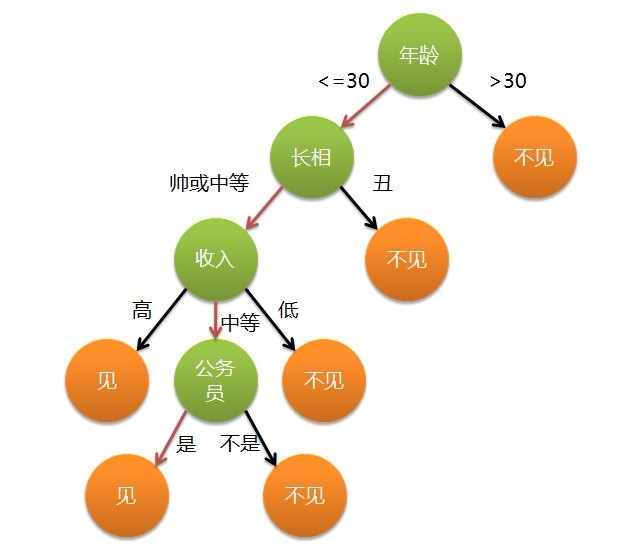
      这个女孩的决策过程就是典型的分类树决策。相当于通过年龄、长相、收入和是否公务员对将男人分为两个类别：见和不见。假设这个女孩对男人的要求是：30岁以下、长相中等以上并且是高收入者或中等以上收入的公务员，那么这个可以用下图表示女孩的决策逻辑：

    也就是说，决策树的简单策略就是，好比公司招聘面试过程中筛选一个人的简历，如果你的条件相当好比如说某985/211重点大学博士毕业，那么二话不说，直接叫过来面试，如果非重点大学毕业，但实际项目经验丰富，那么也要考虑叫过来面试一下，即所谓具体情况具体分析、决策。

第二个例子

    此例子来自Tom M.Mitchell著的机器学习一书：

    小王的目的是通过下周天气预报寻找什么时候人们会打高尔夫，他了解到人们决定是否打球的原因最主要取决于天气情况。而天气状况有晴，云和雨；气温用华氏温度表示；相对湿度用百分比；还有有无风。如此，我们便可以构造一棵决策树，如下（根据天气这个分类决策这天是否合适打网球）：

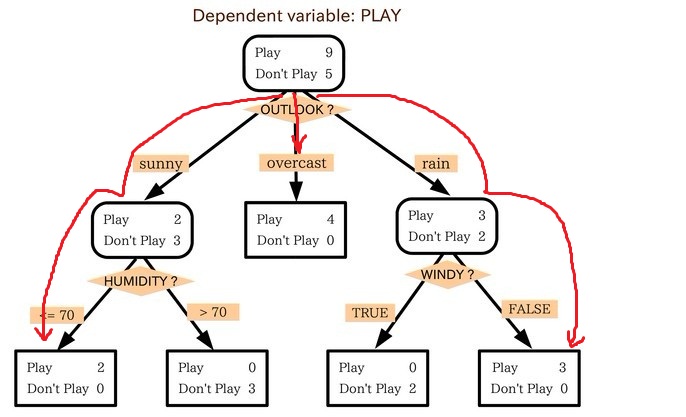
    上述决策树对应于以下表达式：

（Outlook=Sunny ^Humidity<=70）V （Outlook = Overcast）V （Outlook=Rain ^ Wind=Weak）

1.2、ID3算法

1.2.1、ID3算法

    ID3算法是决策树算法的一种。想了解什么是ID3算法之前，我们得先明白一个概念：奥卡姆剃刀。

• 奥卡姆剃刀（Occam's Razor, Ockham's Razor），又称“奥坎的剃刀”，是由14世纪逻辑学家、圣方济各会修士奥卡姆的威廉（William of Occam，约1285年至1349年）提出，他在《箴言书注》2卷15题说“切勿浪费较多东西，去做‘用较少的东西，同样可以做好的事情’。简单点说，便是：be simple。

     ID3算法（Iterative Dichotomiser 3 迭代二叉树3代）是一个由Ross Quinlan发明的用于决策树的算法。这个算法便是建立在上述所介绍的奥卡姆剃刀的基础上：越是小型的决策树越优于大的决策树（be simple简单理论）。尽管如此，该算法也不是总是生成最小的树形结构，而是一个启发式算法。

    OK，从信息论知识中我们知道，期望信息越小，信息增益越大，从而纯度越高。ID3算法的核心思想就是以信息增益度量属性选择，选择分裂后信息增益(很快，由下文你就会知道信息增益又是怎么一回事)最大的属性进行分裂。该算法采用自顶向下的贪婪搜索遍历可能的决策树空间。

     所以，ID3的思想便是：

1. 自顶向下的贪婪搜索遍历可能的决策树空间构造决策树(此方法是ID3算法和C4.5算法的基础)；
2. 从“哪一个属性将在树的根节点被测试”开始；
3. 使用统计测试来确定每一个实例属性单独分类训练样例的能力，分类能力最好的属性作为树的根结点测试。
4. 然后为根结点属性的每个可能值产生一个分支，并把训练样例排列到适当的分支（也就是说，样例的该属性值对应的分支）之下。
5. 重复这个过程，用每个分支结点关联的训练样例来选取在该点被测试的最佳属性。

这形成了对合格决策树的贪婪搜索，也就是算法从不回溯重新考虑以前的选择。

    下图所示即是用于学习布尔函数的ID3算法概要：

1.2.2、哪个属性是最佳的分类属性

1、信息增益的度量标准：熵

    上文中，我们提到：“ID3算法的核心思想就是以信息增益度量属性选择，选择分裂后信息增益(很快，由下文你就会知道信息增益又是怎么一回事)最大的属性进行分裂。”接下来，咱们就来看看这个信息增益是个什么概念。

    上述的ID3算法的核心问题是选取在树的每个结点要测试的属性。我们希望选择的是最有利于分类实例的属性，信息增益(Information Gain)是用来衡量给定的属性区分训练样例的能力，而ID3算法在增长树的每一步使用信息增益从候选属性中选择属性。

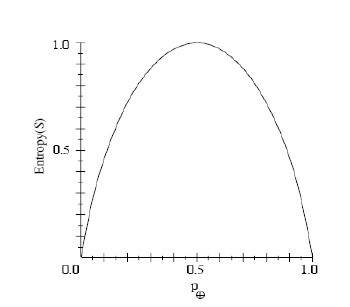
    为了精确地定义信息增益，我们先定义信息论中广泛使用的一个度量标准，称为熵（entropy），它刻画了任意样例集的纯度（purity）。给定包含关于某个目标概念的正反样例的样例集S，那么S相对这个布尔型分类的熵为：

    上述公式中，p+代表正样例，比如在本文开头第一个例子中p+则意味着去打羽毛球，而p-则代表反样例，不去打球(在有关熵的所有计算中我们定义0log0为0)。

    如果写代码实现熵的计算，则如下所示：

1. //根据具体属性和值来计算熵    
2. double ComputeEntropy(vector <vector <string> > remain_state, string attribute, string value,bool ifparent){    
3.     vector<int> count (2,0);    
4.     unsigned int i,j;    
5.     bool done_flag = false;//哨兵值    
6.     for(j = 1; j < MAXLEN; j++){    
7.         if(done_flag) break;    
8.         if(!attribute_row[j].compare(attribute)){    
9.             for(i = 1; i < remain_state.size(); i++){    
10.                 if((!ifparent&&!remain_state[i][j].compare(value)) || ifparent){//ifparent记录是否算父节点    
11.                     if(!remain_state[i][MAXLEN - 1].compare(yes)){    
12.                         count[0]++;    
13.                     }    
14.                     else count[1]++;    
15.                 }    
16.             }    
17.             done_flag = true;    
18.         }    
19.     }    
20.     if(count[0] == 0 || count[1] == 0 ) return 0;//全部是正实例或者负实例    
21.     //具体计算熵 根据[+count[0],-count[1]],log2为底通过换底公式换成自然数底数    
22.     double sum = count[0] + count[1];    
23.     double entropy = -count[0]/sum*log(count[0]/sum)/log(2.0) - count[1]/sum*log(count[1]/sum)/log(2.0);    
24.     return entropy;    
25. }    

    举例来说，假设S是一个关于布尔概念的有14个样例的集合，它包括9个正例和5个反例（我们采用记号[9+，5-]来概括这样的数据样例），那么S相对于这个布尔样例的熵为：

Entropy（[9+，5-]）=-（9/14）log2（9/14）-（5/14）log2（5/14）=0.940。

    So，根据上述这个公式，我们可以得到：S的所有成员属于同一类，Entropy(S)=0； S的正反样例数量相等，Entropy(S)=1；S的正反样例数量不等，熵介于0，1之间，如下图所示：

    信息论中对熵的一种解释，熵确定了要编码集合S中任意成员的分类所需要的最少二进制位数。更一般地，如果目标属性具有c个不同的值，那么S相对于c个状态的分类的熵定义为：

     Pi为子集合中不同性(而二元分类即正样例和负样例)的样例的比例。

2、信息增益度量期望的熵降低

信息增益Gain(S,A)定义

    已经有了熵作为衡量训练样例集合纯度的标准，现在可以定义属性分类训练数据的效力的度量标准。这个标准被称为“信息增益（information gain）”。简单的说，一个属性的信息增益就是由于使用这个属性分割样例而导致的期望熵降低(或者说，样本按照某属性划分时造成熵减少的期望)。更精确地讲，一个属性A相对样例集合S的信息增益Gain(S,A)被定义为：

    其中 Values(A)是属性A所有可能值的集合，是S中属性A的值为v的子集。换句话来讲，Gain(S,A)是由于给定属性A的值而得到的关于目标函数值的信息。当对S的一个任意成员的目标值编码时，Gain(S,A)的值是在知道属性A的值后可以节省的二进制位数。

    接下来，有必要提醒读者一下：关于下面这两个概念 or 公式，

1. 
   
2. 
   

    第一个Entropy(S)是熵定义，第二个则是信息增益Gain(S,A)的定义，而Gain(S,A)由第一个Entropy(S)计算出，记住了。

    下面，举个例子，假定S是一套有关天气的训练样例，描述它的属性包括可能是具有Weak和Strong两个值的Wind。像前面一样，假定S包含14个样例，[9+，5-]。在这14个样例中，假定正例中的6个和反例中的2个有Wind =Weak，其他的有Wind=Strong。由于按照属性Wind分类14个样例得到的信息增益可以计算如下。

    运用在本文开头举得第二个根据天气情况是否决定打羽毛球的例子上，得到的最佳分类属性如下图所示：

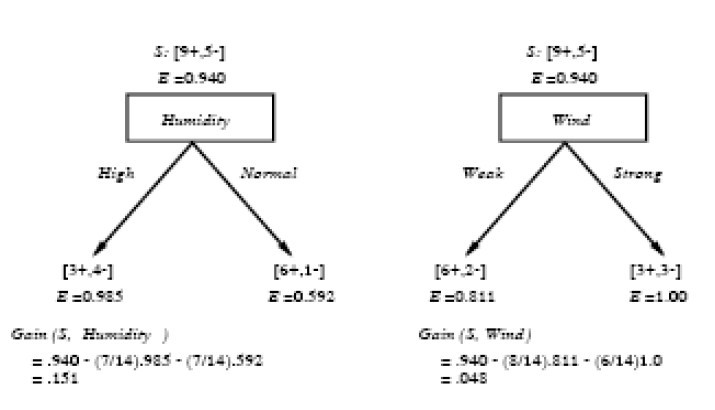
     在上图中，计算了两个不同属性：湿度(humidity)和风力(wind)的信息增益，最终humidity这种分类的信息增益0.151>wind增益的0.048。说白了，就是在星期六上午是否适合打网球的问题诀策中，采取humidity较wind作为分类属性更佳，决策树由此而来。

1. //计算信息增益，DFS构建决策树    
2. //current_node为当前的节点    
3. //remain_state为剩余待分类的样例    
4. //remian_attribute为剩余还没有考虑的属性    
5. //返回根结点指针    
6. Node * BulidDecisionTreeDFS(Node * p, vector <vector <string> > remain_state, vector <string> remain_attribute){    
7.     //if(remain_state.size() > 0){    
8.         //printv(remain_state);    
9.     //}    
10.     if (p == NULL)    
11.         p = new Node();    
12.     //先看搜索到树叶的情况    
13.     if (AllTheSameLabel(remain_state, yes)){    
14.         p->attribute = yes;    
15.         return p;    
16.     }    
17.     if (AllTheSameLabel(remain_state, no)){    
18.         p->attribute = no;    
19.         return p;    
20.     }    
21.     if(remain_attribute.size() == 0){//所有的属性均已经考虑完了,还没有分尽    
22.         string label = MostCommonLabel(remain_state);    
23.         p->attribute = label;    
24.         return p;    
25.     }    
26.     
27.     double max_gain = 0, temp_gain;    
28.     vector <string>::iterator max_it;    
29.     vector <string>::iterator it1;    
30.     for(it1 = remain_attribute.begin(); it1 < remain_attribute.end(); it1++){    
31.         temp_gain = ComputeGain(remain_state, (*it1));    
32.         if(temp_gain > max_gain) {    
33.             max_gain = temp_gain;    
34.             max_it = it1;    
35.         }    
36.     }    
37.     //下面根据max_it指向的属性来划分当前样例，更新样例集和属性集    
38.     vector <string> new_attribute;    
39.     vector <vector <string> > new_state;    
40.     for(vector <string>::iterator it2 = remain_attribute.begin(); it2 < remain_attribute.end(); it2++){    
41.         if((*it2).compare(*max_it)) new_attribute.push_back(*it2);    
42.     }    
43.     //确定了最佳划分属性，注意保存    
44.     p->attribute = *max_it;    
45.     vector <string> values = map_attribute_values[*max_it];    
46.     int attribue_num = FindAttriNumByName(*max_it);    
47.     new_state.push_back(attribute_row);    
48.     for(vector <string>::iterator it3 = values.begin(); it3 < values.end(); it3++){    
49.         for(unsigned int i = 1; i < remain_state.size(); i++){    
50.             if(!remain_state[i][attribue_num].compare(*it3)){    
51.                 new_state.push_back(remain_state[i]);    
52.             }    
53.         }    
54.         Node * new_node = new Node();    
55.         new_node->arrived_value = *it3;    
56.         if(new_state.size() == 0){//表示当前没有这个分支的样例，当前的new_node为叶子节点    
57.             new_node->attribute = MostCommonLabel(remain_state);    
58.         }    
59.         else     
60.             BulidDecisionTreeDFS(new_node, new_state, new_attribute);    
61.         //递归函数返回时即回溯时需要1 将新结点加入父节点孩子容器 2清除new_state容器    
62.         p->childs.push_back(new_node);    
63.         new_state.erase(new_state.begin()+1,new_state.end());//注意先清空new_state中的前一个取值的样例，准备遍历下一个取值样例    
64.     }    
65.     return p;    
66. }    

1.2.3、ID3算法决策树的形成

    OK，下图为ID3算法第一步后形成的部分决策树。这样综合起来看，就容易理解多了。1、overcast样例必为正，所以为叶子结点，总为yes；2、ID3无回溯，局部最优，而非全局最优，还有另一种树后修剪决策树。下图是ID3算法第一步后形成的部分决策树：

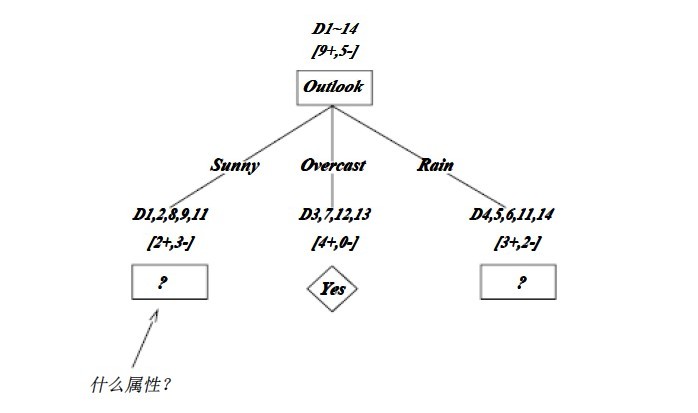
    如上图，训练样例被排列到对应的分支结点。分支Overcast的所有样例都是正例，所以成为目标分类为Yes的叶结点。另两个结点将被进一步展开，方法是按照新的样例子集选取信息增益最高的属性。

1.3、C4.5算法

1.3.1、C4.5算法的改进

    C4.5，是机器学习算法中的另一个分类决策树算法，它是决策树(决策树也就是做决策的节点间的组织方式像一棵树，其实是一个倒树)核心算法，也是上文1.2节所介绍的ID3的改进算法，所以基本上了解了一半决策树构造方法就能构造它。

    决策树构造方法其实就是每次选择一个好的特征以及分裂点作为当前节点的分类条件。

    既然说C4.5算法是ID3的改进算法，那么C4.5相比于ID3改进的地方有哪些呢？：

1. 用信息增益率来选择属性。ID3选择属性用的是子树的信息增益，这里可以用很多方法来定义信息，ID3使用的是熵(entropy，熵是一种不纯度度量准则),也就是熵的变化值，而C4.5用的是信息增益率。对，区别就在于一个是信息增益，一个是信息增益率。
2. 在树构造过程中进行剪枝，在构造决策树的时候，那些挂着几个元素的节点，不考虑最好，不然容易导致overfitting。
3. 对非离散数据也能处理。
4. 能够对不完整数据进行处理

    针对上述第一点，解释下：一般来说率就是用来取平衡用的，就像方差起的作用差不多，比如有两个跑步的人，一个起点是10m/s的人、其10s后为20m/s；另一个人起速是1m/s、其1s后为2m/s。如果紧紧算差值那么两个差距就很大了，如果使用速度增加率(加速度，即都是为1m/s^2)来衡量，2个人就是一样的加速度。因此，C4.5克服了ID3用信息增益选择属性时偏向选择取值多的属性的不足。

C4.5算法之信息增益率

    OK，既然上文中提到C4.5用的是信息增益率，那增益率的具体是如何定义的呢？：

    是的，在这里，C4.5算法不再是通过信息增益来选择决策属性。一个可以选择的度量标准是增益比率gain ratio（Quinlan 1986）。增益比率度量是用前面的增益度量Gain(S，A)和分裂信息度量SplitInformation(S，A)来共同定义的，如下所示：

    其中，分裂信息度量被定义为(分裂信息用来衡量属性分裂数据的广度和均匀)：

   

    其中S1到Sc是c个值的属性A分割S而形成的c个样例子集。注意分裂信息实际上就是S关于属性A的各值的熵。这与我们前面对熵的使用不同，在那里我们只考虑S关于学习到的树要预测的目标属性的值的熵。

    请注意，分裂信息项阻碍选择值为均匀分布的属性。例如，考虑一个含有n个样例的集合被属性A彻底分割（译注：分成n组，即一个样例一组）。这时分裂信息的值为log2n。相反，一个布尔属性B分割同样的n个实例，如果恰好平分两半，那么分裂信息是1。如果属性A和B产生同样的信息增益，那么根据增益比率度量，明显B会得分更高。

    使用增益比率代替增益来选择属性产生的一个实际问题是，当某个Si接近S（|Si|»|S|）时分母可能为0或非常小。如果某个属性对于S的所有样例有几乎同样的值，这时要么导致增益比率未定义，要么是增益比率非常大。为了避免选择这种属性，我们可以采用这样一些启发式规则，比如先计算每个属性的增益，然后仅对那些增益高过平均值的属性应用增益比率测试（Quinlan 1986）。

    除了信息增益，Lopez de Mantaras（1991）介绍了另一种直接针对上述问题而设计的度量，它是基于距离的（distance-based）。这个度量标准基于所定义的一个数据划分间的距离尺度。具体更多请参看：Tom M.Mitchhell所著的机器学习之3.7.3节。

1.3.2、C4.5算法构造决策树的过程

1. Function C4.5(R:包含连续属性的无类别属性集合,C:类别属性,S:训练集)  
2. /*返回一棵决策树*/  
3. Begin  
4.    If S为空,返回一个值为Failure的单个节点;  
5.    If S是由相同类别属性值的记录组成,  
6.       返回一个带有该值的单个节点;  
7.    If R为空,则返回一个单节点,其值为在S的记录中找出的频率最高的类别属性值;  
8.    [注意未出现错误则意味着是不适合分类的记录]；  
9.   For 所有的属性R(Ri) Do  
10.         If 属性Ri为连续属性，则  
11.      Begin  
12.            将Ri的最小值赋给A1：  
13.         将Rm的最大值赋给Am；/*m值手工设置*/  
14.            For j From 2 To m-1 Do Aj=A1+j*(A1Am)/m;  
15.            将Ri点的基于{< =Aj,>Aj}的最大信息增益属性(Ri,S)赋给A；  
16.      End；  
17.   将R中属性之间具有最大信息增益的属性(D,S)赋给D;  
18.    将属性D的值赋给{dj/j=1,2...m}；  
19.   将分别由对应于D的值为dj的记录组成的S的子集赋给{sj/j=1,2...m};  
20.    返回一棵树，其根标记为D;树枝标记为d1,d2...dm;  
21.    再分别构造以下树:  
22.    C4.5(R-{D},C,S1),C4.5(R-{D},C,S2)...C4.5(R-{D},C,Sm);  
23. End C4.5  

1.3.3、C4.5算法实现中的几个关键步骤

    在上文中，我们已经知道了决策树学习中两个重要概念的表达，如下：

1. 
2. 

    接下来，咱们写下代码实现，

    1、信息熵

1. double C4_5::entropy(int *attrClassCount, int classNum, int allNum){  
2.     double iEntropy = 0.0;  
3.     for(int i = 0; i < classNum; i++){  
4.         double temp = ((double)attrClassCount[i]) / allNum;  
5.         if(temp != 0.0)  
6.             iEntropy -= temp * (log(temp) / log(2.0));  
7.     }  
8.     return iEntropy;  
9. }  

    2、信息增益率

1. double C4_5::gainRatio(int classNum, vector<int *> attriCount, double pEntropy){  
2.     int* attriNum = new int[attriCount.size()];  
3.     int allNum = 0;  
4.   
5.     for(int i = 0; i < (int)attriCount.size(); i++){  
6.         attriNum[i] = 0;  
7.         for(int j = 0; j < classNum; j++){  
8.             attriNum[i] += attriCount[i][j];  
9.             allNum += attriCount[i][j];  
10.         }  
11.     }  
12.     double gain = 0.0;  
13.     double splitInfo = 0.0;  
14.     for(int i = 0; i < (int)attriCount.size(); i++){  
15.         gain -= ((double)attriNum[i]) / allNum * entropy(attriCount[i], classNum, attriNum[i]);  
16.         splitInfo -= ((double)attriNum[i]) / allNum * (log(((double)attriNum[i])/allNum) / log(2.0));  
17.     }  
18.     gain += pEntropy;  
19.     delete[] attriNum;   
20.     return (gain / splitInfo);  
21. }  

    3、选取最大增益属性作为分类条件

1. int C4_5::chooseAttribute(vector<int> attrIndex, vector<int *>* sampleCount){  
2.     int bestIndex = 0;  
3.     double maxGainRatio = 0.0;  
4.     int classNum = (int)(decisions[attrIndex[(int)attrIndex.size()-1]]).size();//number of class  
5.   
6.     //computer the class entropy  
7.     int* temp = new int[classNum];  
8.     int allNum = 0;  
9.     for(int i = 0; i < classNum; i++){  
10.         temp[i] = sampleCount[(int)attrIndex.size()-1][i][i];  
11.         allNum += temp[i];  
12.     }  
13.     double pEntropy = entropy(temp, classNum, allNum);  
14.     delete[] temp;  
15.   
16.     //computer gain ratio for every attribute  
17.     for(int i = 0; i < (int)attrIndex.size()-1; i++){  
18.         double gainR = gainRatio(classNum, sampleCount[i], pEntropy);  
19.         if(gainR > maxGainRatio){  
20.             bestIndex = i;  
21.             maxGainRatio = gainR;  
22.         }  
23.     }  
24.     return bestIndex;  
25. }  

    4、还有一系列建树，打印树的步骤，此处略过。

1.4、决策树归纳的特点

第二部分、贝叶斯分类

    说实话，友人刘未鹏有一篇讲的贝叶斯的文章：数学之美番外篇：平凡而又神奇的贝叶斯方法，已经把贝叶斯讲的很清晰透彻了，我再讲也是如李白看到崔颢在黄鹤楼上所提的：登黄鹤楼

昔人已乘黄鹤去，此地空余黄鹤楼；

黄鹤一去不复返，白云千载空悠悠。

    后便大为折服，已无什兴致再提了，偶现在就是这感觉。然文章还得继续写，那就权当是对它的一个总结或整理吧，有任何不妥之处，还望读者和未鹏兄海涵，谢谢。

2.1、什么是贝叶斯分类

   贝叶斯定理：已知某条件概率，如何得到两个事件交换后的概率，也就是在已知P(A|B)的情况下如何求得P(B|A)。这里先解释什么是条件概率：

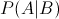      表示事件B已经发生的前提下，事件A发生的概率，叫做事件B发生下事件A的条件概率。其基本求解公式为：。

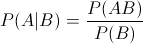      贝叶斯定理之所以有用，是因为我们在生活中经常遇到这种情况：我们可以很容易直接得出P(A|B)，P(B|A)则很难直接得出，但我们更关心P(B|A)，贝叶斯定理就为我们打通从P(A|B)获得P(B|A)的道路。

      下面不加证明地直接给出贝叶斯定理（公式被网友指出有问题，待后续验证改正）：

      

     So，其一般形式就是：

P(A|B) = P(A|B) * P(B) / [P(A|B) * P(B) + P(A|~B) * P(~B) ]

    收缩起来就是：

P(A|B) = P(AB) / P(B)

    其实这个就等于：

P(A|B) * P(B) = P(AB)

    然看似这么平凡的贝叶斯公式，背后却隐含着非常深刻的原理。

2.2、贝叶斯的应用

2.2.1、中文分词

    贝叶斯是机器学习的核心方法之一。比如中文分词领域就用到了贝叶斯。浪潮之巅的作者吴军在《数学之美》系列中就有一篇是介绍中文分词的。这里介绍一下核心的思想，不做赘述，详细请参考吴军的原文。

    分词问题的描述为：给定一个句子（字串），如：

    结构之法算法之道

    如何对这个句子进行分词（词串）才是最靠谱的。例如：

1. 南京市/长江大桥

2. 南京/市长/江大桥

    这两个分词，到底哪个更靠谱呢？

    我们用贝叶斯公式来形式化地描述这个问题，令 X 为字串（句子），Y 为词串（一种特定的分词假设）。我们就是需要寻找使得 P(Y|X) 最大的 Y ，使用一次贝叶斯可得：

    P(Y|X) ∝ P(Y)*P(X|Y)

     用自然语言来说就是 这种分词方式（词串）的可能性 乘以 这个词串生成我们的句子的可能性。我们进一步容易看到：可以近似地将 P(X|Y) 看作是恒等于 1 的，因为任意假想的一种分词方式之下生成我们的句子总是精准地生成的（只需把分词之间的分界符号扔掉即可）。于是，我们就变成了去最大化 P(Y) ，也就是寻找一种分词使得这个词串（句子）的概率最大化。而如何计算一个词串：

    W1, W2, W3, W4 ..

    的可能性呢？我们知道，根据联合概率的公式展开：P(W1, W2, W3, W4 ..) = P(W1) * P(W2|W1) * P(W3|W2, W1) * P(W4|W1,W2,W3) * .. 于是我们可以通过一系列的条件概率（右式）的乘积来求整个联合概率。然而不幸的是随着条件数目的增加（P(Wn|Wn-1,Wn-2,..,W1) 的条件有 n-1 个），数据稀疏问题也会越来越严重，即便语料库再大也无法统计出一个靠谱的 P(Wn|Wn-1,Wn-2,..,W1) 来。为了缓解这个问题，计算机科学家们一如既往地使用了“天真”假设：我们假设句子中一个词的出现概率只依赖于它前面的有限的 k 个词（k 一般不超过 3，如果只依赖于前面的一个词，就是2元语言模型（2-gram），同理有 3-gram 、 4-gram 等），这个就是所谓的“有限地平线”假设。

     虽然上面这个假设很傻很天真，但结果却表明它的结果往往是很好很强大的，后面要提到的朴素贝叶斯方法使用的假设跟这个精神上是完全一致的，我们会解释为什么像这样一个天真的假设能够得到强大的结果。目前我们只要知道，有了这个假设，刚才那个乘积就可以改写成： P(W1) * P(W2|W1) * P(W3|W2) * P(W4|W3) .. （假设每个词只依赖于它前面的一个词）。而统计 P(W2|W1) 就不再受到数据稀疏问题的困扰了。对于我们上面提到的例子“南京市长江大桥”，如果按照自左到右的贪婪方法分词的话，结果就成了“南京市长/江大桥”。但如果按照贝叶斯分词的话（假设使用 3-gram），由于“南京市长”和“江大桥”在语料库中一起出现的频率为 0 ，这个整句的概率便会被判定为 0 。 从而使得“南京市/长江大桥”这一分词方式胜出。

2.2.2、贝叶斯图像识别，Analysis by Synthesis

    贝叶斯方法是一个非常 general 的推理框架。其核心理念可以描述成：Analysis by Synthesis （通过合成来分析）。06 年的认知科学新进展上有一篇 paper 就是讲用贝叶斯推理来解释视觉识别的，一图胜千言，下图就是摘自这篇 paper ：

    首先是视觉系统提取图形的边角特征，然后使用这些特征自底向上地激活高层的抽象概念（比如是 E 还是 F 还是等号），然后使用一个自顶向下的验证来比较到底哪个概念最佳地解释了观察到的图像。

2.2.3、EM 算法与基于模型的聚类

     聚类是一种无指导的机器学习问题，问题描述：给你一堆数据点，让你将它们最靠谱地分成一堆一堆的。聚类算法很多，不同的算法适应于不同的问题，这里仅介绍一个基于模型的聚类，该聚类算法对数据点的假设是，这些数据点分别是围绕 K 个核心的 K 个正态分布源所随机生成的，使用 Han JiaWei 的《Data Ming： Concepts and Techniques》中的图：

    图中有两个正态分布核心，生成了大致两堆点。我们的聚类算法就是需要根据给出来的那些点，算出这两个正态分布的核心在什么位置，以及分布的参数是多少。这很明显又是一个贝叶斯问题，但这次不同的是，答案是连续的且有无穷多种可能性，更糟的是，只有当我们知道了哪些点属于同一个正态分布圈的时候才能够对这个分布的参数作出靠谱的预测，现在两堆点混在一块我们又不知道哪些点属于第一个正态分布，哪些属于第二个。反过来，只有当我们对分布的参数作出了靠谱的预测时候，才能知道到底哪些点属于第一个分布，那些点属于第二个分布。这就成了一个先有鸡还是先有蛋的问题了。为了解决这个循环依赖，总有一方要先打破僵局，说，不管了，我先随便整一个值出来，看你怎么变，然后我再根据你的变化调整我的变化，然后如此迭代着不断互相推导，最终收敛到一个解。这就是 EM 算法。

    EM 的意思是“Expectation-Maximazation”，在这个聚类问题里面，我们是先随便猜一下这两个正态分布的参数：如核心在什么地方，方差是多少。然后计算出每个数据点更可能属于第一个还是第二个正态分布圈，这个是属于 Expectation 一步。有了每个数据点的归属，我们就可以根据属于第一个分布的数据点来重新评估第一个分布的参数（从蛋再回到鸡），这个是 Maximazation 。如此往复，直到参数基本不再发生变化为止。这个迭代收敛过程中的贝叶斯方法在第二步，根据数据点求分布的参数上面。

2.2.4、最大似然与最小二乘

    学过线性代数的大概都知道经典的最小二乘方法来做线性回归。问题描述是：给定平面上 N 个点，（这里不妨假设我们想用一条直线来拟合这些点——回归可以看作是拟合的特例，即允许误差的拟合），找出一条最佳描述了这些点的直线。

    一个接踵而来的问题就是，我们如何定义最佳？我们设每个点的坐标为 (Xi, Yi) 。如果直线为 y = f(x) 。那么 (Xi, Yi) 跟直线对这个点的“预测”：(Xi, f(Xi)) 就相差了一个 ΔYi = |Yi – f(Xi)| 。最小二乘就是说寻找直线使得 (ΔY1)^2 + (ΔY2)^2 + .. （即误差的平方和）最小，至于为什么是误差的平方和而不是误差的绝对值和，统计学上也没有什么好的解释。然而贝叶斯方法却能对此提供一个完美的解释。

    我们假设直线对于坐标 Xi 给出的预测 f(Xi) 是最靠谱的预测，所有纵坐标偏离 f(Xi) 的那些数据点都含有噪音，是噪音使得它们偏离了完美的一条直线，一个合理的假设就是偏离路线越远的概率越小，具体小多少，可以用一个正态分布曲线来模拟，这个分布曲线以直线对 Xi 给出的预测 f(Xi) 为中心，实际纵坐标为 Yi 的点 (Xi, Yi) 发生的概率就正比于 EXP[-(ΔYi)^2]。（EXP(..) 代表以常数 e 为底的多少次方）。

    现在我们回到问题的贝叶斯方面，我们要想最大化的后验概率是：

P(h|D) ∝ P(h) * P(D|h)

    又见贝叶斯！这里 h 就是指一条特定的直线，D 就是指这 N 个数据点。我们需要寻找一条直线 h 使得 P(h) * P(D|h) 最大。很显然，P(h) 这个先验概率是均匀的，因为哪条直线也不比另一条更优越。所以我们只需要看 P(D|h) 这一项，这一项是指这条直线生成这些数据点的概率，刚才说过了，生成数据点 (Xi, Yi) 的概率为 EXP[-(ΔYi)^2] 乘以一个常数。而 P(D|h) = P(d1|h) * P(d2|h) * .. 即假设各个数据点是独立生成的，所以可以把每个概率乘起来。于是生成 N 个数据点的概率为 EXP[-(ΔY1)^2] * EXP[-(ΔY2)^2] * EXP[-(ΔY3)^2] * .. = EXP{-[(ΔY1)^2 + (ΔY2)^2 + (ΔY3)^2 + ..]} 最大化这个概率就是要最小化 (ΔY1)^2 + (ΔY2)^2 + (ΔY3)^2 + .. 。 熟悉这个式子吗？

2.3、朴素贝叶斯方法

    朴素贝叶斯方法是一个很特别的方法，所以值得介绍一下。我们用朴素贝叶斯在垃圾邮件过滤中的应用来举例说明。

2.3.1、贝叶斯垃圾邮件过滤器

    问题是什么？问题是，给定一封邮件，判定它是否属于垃圾邮件。按照先例，我们还是用 D 来表示这封邮件，注意 D 由 N 个单词组成。我们用 h+ 来表示垃圾邮件，h- 表示正常邮件。问题可以形式化地描述为求：

P(h+|D) = P(h+) * P(D|h+) / P(D)

P(h-|D) = P(h-) * P(D|h-) / P(D)

    其中 P(h+) 和 P(h-) 这两个先验概率都是很容易求出来的，只需要计算一个邮件库里面垃圾邮件和正常邮件的比例就行了。然而 P(D|h+) 却不容易求，因为 D 里面含有 N 个单词 d1, d2, d3, .. ，所以P(D|h+) = P(d1,d2,..,dn|h+) 。我们又一次遇到了数据稀疏性，为什么这么说呢？P(d1,d2,..,dn|h+) 就是说在垃圾邮件当中出现跟我们目前这封邮件一模一样的一封邮件的概率是多大！开玩笑，每封邮件都是不同的，世界上有无穷多封邮件。瞧，这就是数据稀疏性，因为可以肯定地说，你收集的训练数据库不管里面含了多少封邮件，也不可能找出一封跟目前这封一模一样的。结果呢？我们又该如何来计算 P(d1,d2,..,dn|h+) 呢？

    我们将 P(d1,d2,..,dn|h+)  扩展为： P(d1|h+) * P(d2|d1, h+) * P(d3|d2,d1, h+) * .. 。熟悉这个式子吗？这里我们会使用一个更激进的假设，我们假设 di 与 di-1 是完全条件无关的，于是式子就简化为 P(d1|h+) * P(d2|h+) * P(d3|h+) * .. 。这个就是所谓的条件独立假设，也正是朴素贝叶斯方法的朴素之处。而计算 P(d1|h+) * P(d2|h+) * P(d3|h+) * .. 就太简单了，只要统计 di 这个单词在垃圾邮件中出现的频率即可。关于贝叶斯垃圾邮件过滤更多的内容可以参考这个条目，注意其中提到的其他资料。

2.3.2、为什么朴素贝叶斯方法令人诧异地好——一个理论解释

    朴素贝叶斯方法的条件独立假设看上去很傻很天真，为什么结果却很好很强大呢？就拿一个句子来说，我们怎么能鲁莽地声称其中任意一个单词出现的概率只受到它前面的 3 个或 4 个单词的影响呢？别说 3 个，有时候一个单词的概率受到上一句话的影响都是绝对可能的。那么为什么这个假设在实际中的表现却不比决策树差呢？有人对此提出了一个理论解释，并且建立了什么时候朴素贝叶斯的效果能够等价于非朴素贝叶斯的充要条件，这个解释的核心就是：有些独立假设在各个分类之间的分布都是均匀的所以对于似然的相对大小不产生影响；即便不是如此，也有很大的可能性各个独立假设所产生的消极影响或积极影响互相抵消，最终导致结果受到的影响不大。具体的数学公式请参考这篇 paper 。

2.4、层级贝叶斯模型

    层级贝叶斯模型是现代贝叶斯方法的标志性建筑之一。前面讲的贝叶斯，都是在同一个事物层次上的各个因素之间进行统计推理，然而层次贝叶斯模型在哲学上更深入了一层，将这些因素背后的因素（原因的原因，原因的原因，以此类推）囊括进来。一个教科书例子是：如果你手头有 N 枚硬币，它们是同一个工厂铸出来的，你把每一枚硬币掷出一个结果，然后基于这 N 个结果对这 N 个硬币的 θ （出现正面的比例）进行推理。如果根据最大似然，每个硬币的 θ 不是 1 就是 0 （这个前面提到过的），然而我们又知道每个硬币的 p(θ) 是有一个先验概率的，也许是一个 beta 分布。也就是说，每个硬币的实际投掷结果 Xi 服从以 θ 为中心的正态分布，而 θ 又服从另一个以 Ψ 为中心的 beta 分布。层层因果关系就体现出来了。进而 Ψ 还可能依赖于因果链上更上层的因素，以此类推。

2.5、隐马可夫模型（HMM）

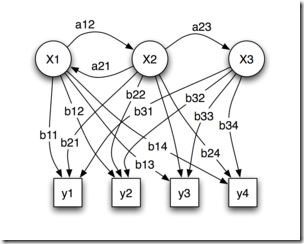
    吴军在数学之美系列里面介绍的隐马可夫模型（HMM）就是一个简单的层级贝叶斯模型：

那么怎么根据接收到的信息来推测说话者想表达的意思呢？我们可以利用叫做“隐含马尔可夫模型”（Hidden Markov Model）来解决这些问题。以语音识别为例，当我们观测到语音信号 o1,o2,o3 时，我们要根据这组信号推测出发送的句子 s1,s2,s3。显然，我们应该在所有可能的句子中找最有可能性的一个。用数学语言来描述，就是在已知 o1,o2,o3,…的情况下，求使得条件概率 P (s1,s2,s3,…|o1,o2,o3….) 达到最大值的那个句子 s1,s2,s3,…

    吴军的文章中这里省掉没说的是，s1, s2, s3, .. 这个句子的生成概率同时又取决于一组参数，这组参数决定了 s1, s2, s3, .. 这个马可夫链的先验生成概率。如果我们将这组参数记为 λ ，我们实际上要求的是：P(S|O, λ) （其中 O 表示 o1,o2,o3,.. ，S表示 s1,s2,s3,..）

当然，上面的概率不容易直接求出，于是我们可以间接地计算它。利用贝叶斯公式并且省掉一个常数项，可以把上述公式等价变换成

P(o1,o2,o3,…|s1,s2,s3….) * P(s1,s2,s3,…)

其中

P(o1,o2,o3,…|s1,s2,s3….) 表示某句话 s1,s2,s3…被读成 o1,o2,o3,…的可能性, 而 P(s1,s2,s3,…) 表示字串 s1,s2,s3,…本身能够成为一个合乎情理的句子的可能性，所以这个公式的意义是用发送信号为 s1,s2,s3…这个数列的可能性乘以 s1,s2,s3.. 本身可以一个句子的可能性，得出概率。

    这里，s1,s2,s3…本身可以一个句子的可能性其实就取决于参数 λ ，也就是语言模型。所以简而言之就是发出的语音信号取决于背后实际想发出的句子，而背后实际想发出的句子本身的独立先验概率又取决于语言模型。更多具体细节请参考未鹏兄之：数学之美番外篇：平凡而又神奇的贝叶斯方法。

后记

    促成自己写这篇文章乃至整个聚类 & 分类算法系列的有3个因素，

1. 一的确是如本文开头所说，在最近参加的一些面试中被问到描述自己所知道或了解的聚类 & 分类算法(当然，这完全不代表你将来的面试中会遇到此类问题，只是因为我的简历上写了句熟悉常见的聚类 & 分类算法而已)，
2. 二则是之前去一家公司面试，他们有数据挖掘工程师的岗位，原来是真有那么一群人是专门负责数据分析，算法决策与调研的，情不自禁的对数据挖掘产生了不浅兴趣；
3. 三则是手头上有两本这样的经典书籍：机器学习 & 数据挖掘导论，看看又何妨呢，看的同时写写文章，做做笔记，备忘录又有何不可呢？

    OK，最后一件事：关于读书会第3期周爱民 & 梁斌，时间：本周日5月20日下午2点，地点：北大二教527。报名：发姓名 + 公司职位 or 学校专业 + 专注方向至邮箱：[e-mail]。详情，请参见此文：读书会·北京：最新第3期05.20下午周爱民 ，梁斌penny于北大举办。欢迎朋友们的到来。

    本文或本聚类 & 分类算法系列中任何一篇文章有任何问题，漏洞，或bug，欢迎任何读者随时不吝赐教 & 指正，感谢大家，谢谢。完。July、二零一二年五月十八日凌晨二点半。