二项堆

<1>. 二项堆数据结构简介

一颗二项堆是由一组二项树组成，在给出二项堆的定义之前，首先我们来定义什么是二项树。

二项树是一种递归的定义:

1. 二项树B[0]仅仅包含一个节点

2. B[k]是由两棵B[k-1]二项树组成，其中一颗树是另外一颗树的子树。

下面是B0 - B4二项树：

 

显然二项树具有如下的性质：

1. 对于树B[k]该树含有2^k个节点；

2.  树的高度是k；

3. 在深度为i中含有C_i^k节点，其中i = 0， 1，2 ... , k;

定义完二项树之后，下面来定义二项堆H，二项堆是由一组满足下面的二项树组成：

1.  H中的每个二项树遵循最小堆性质；

2. 对于任意的整数k的话，在H不存在另外一个度数也是k的二项树；

另外定义：

1. 二项堆的度数定义成子女个数；

2. 定义二项堆的根表是二项树的根节点形成的链表； 

以上第一个性质保证了二项树的根结点包含了最小的关键字。第二个性质则说明结点数为的二项堆最多只有棵二项树。

示例：一个含13个结点的二项堆

<2>. 存储模型 

了解了什么二项堆的定义和使用场景之后，我们来看看如何存储二项堆？

首先定义二项堆中每个节点的类型：

1. parent：指向父节点

2. sibling：指向右边的兄弟节点

3. child：定义该节点的子节点

4. degree:定义该节点的度数

5. 其他应用场景中需要的数据

struct heap_node {

struct heap_node* parent;

struct heap_node* next;

struct heap_node* child;

unsigned int degree;

void*value;

struct heap_node**ref;

}; 

对于定义的字段，对于根表中的节点和非根表中的元素是不相同的，根表中的节点的parent全部是空，sibling指向的是根表中的下一个元素；对于非根表中的节点的话，parent指向的是该节点的父节点，sibling指向该节点的兄弟节点。

定义二项堆数据类型：

1. 根表的头节点

2. 其他应用需要的数据 

struct heap {

struct heap_node* head;

struct heap_node*min;

}; 

<3>. 算法分析 

3.1 初始化二项堆

 仅仅将根表的头节点指向null：

static inline void heap_init(struct heap* heap)

{

heap->head = NULL;

heap->min  = NULL;// 其他操作

} 

3.2 寻找最小关键字

由于二项堆中每个二项树都是遵循最小堆性质的，所以最小元素一定是在根表中，遍历根表一次即可找出最小元素：

// 通过node返回二项堆中的最小元素，同时

// 通过prev指针返回最小元素node的前一个节点

// 指针

static inline void __heap_min(heap_prio_t higher_prio, struct heap* heap,

      struct heap_node** prev, struct heap_node** node)

{

struct heap_node *_prev, *cur;

*prev = NULL;

    // 如果二项堆为空

if (!heap->head) {

*node = NULL;

return;

}

*node = heap->head; // 保存最小元素节点指针,初始默认head是最小

_prev = heap->head; // 前一个节点指针

cur   = heap->head->next;

while (cur) {

if (higher_prio(cur, *node)) {

    // 找到更小的节点

*node = cur;

*prev = _prev;

}

_prev = cur;

cur   = cur->next;

}

}

3.3 合并操作

二项堆的合并操作是一个比较复杂的过程，这里假设需要合并的两个二项堆是H1和H2，如果简单的将H1和H2的根表（两个链表）进行合并的话，显然这可能是违反了二项堆定义的第二条，这就是二项堆合并操作的主要需要解决的问题：两个二项堆合并完成之后，可能在根表中存在两个度数相同的节点，需要将度数相同的节点合并成一个新的节点。

这里我们进一步将这个问题现在转换成了：已知H1根表和H2的根表中每个节点的度数，并且H1和H2的根表已经是按照度数排序的，如何H1和H2根表合并，并且新的根表中不存在两个度数相同的节点。

最基本的为二个度数相同的二项树的合并。由于二项树根结点包含最小的关键字，因此在二颗树合并时，只需比较二个根结点关键字的大小，其中含小关键字的结点成为结果树的根结点，另一棵树则变成结果树的子树。

function mergeTree(p, q)    if p.root <= q.root        return p.addSubTree(q)    else        return q.addSubTree(p)

两个二项堆的合并则可按如下步骤进行：度数从小取到大，在两个二项堆中如果其中只有一棵树的度数为，即将此树移动到结果堆，而如果只两棵树的度数都为，则根据以上方法合并为一个度数为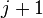的二项树。此后这个度数为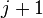的树将可能会和其他度数为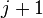的二项树进行合并。

此操作的时间复杂度为。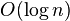

3.4插入

创建一个只包含要插入关键字的堆，再将此堆与原先的二项堆进行合并，即可得到插入后的堆。由于需要合并，插入操作需要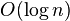的时间。

3.5删除最小关键字所在结点

先找到最小关键字所在结点，然后将它从其所在的二项树中删除，并获得其子树。将这些子树看作一个独立的二项堆，再将此堆合并到原先的堆中即可。由于每棵树最多有棵子树，创建新堆的时间为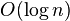。同时合并堆的时间也为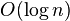，故整个操作所需时间为。

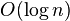function deleteMin(heap)    min = heap.trees().first()    for each current in heap.trees()        if current.root < min then min = current    for each tree in min.subTrees()        tmp.addTree(tree)

3.6减小关键字的值

在减小关键字的值后，可能会不满足最小堆性质。此时，将其所在结点与父结点交换关键字，如还不满足最小堆性质则再与祖父结点交换关键字……直到最小堆性质得到满足。操作所需时间为。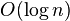

3.7删除

将需要删除的结点的关键字的值减小到负无穷大（比二项堆中的其他所有关键字的值都小即可），再删除最小关键字的结点即可。