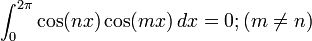DCT原型 ——傅里叶级数

来源：互联网发布：手机扩音器软件下载编辑：程序博客网时间：2024/04/29 18:02

傅里叶级数

法国数学家傅里叶发现，任何周期函数都可以用正弦函数和余弦函数构成的无穷级数来表示（选择正弦函数与余弦函数作为基函数是因为它们是正交的），后世称为傅里叶级数（法语：série de Fourier，或译为傅里叶级数）。傅里叶级数在数论、组合数学、信号处理、概率论、统计学、密码学、声学、光学等领域都有着广泛的应用。

傅里叶级数的公式

给定一个周期为T的函数x(t)，那么它可以表示为无穷级数：

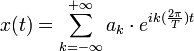$x(t)=\sum _{k=-\infty}^{+\infty}a_k\cdot e^{ik(\frac{2\pi}{T})t}$ （i为虚数单位）（1）

其中， $a_k$ 可以按下式计算：

$a_k=\frac{1}{T}\int_{T}x(t)\cdot e^{-ik(\frac{2\pi}{T})t}dt$ （2）

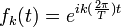注意到 $f_k(t)=e^{ik(\frac{2\pi}{T})t}$ 是周期为T的函数，故k 取不同值时的周期信号具有谐波关系（即它们都具有一个共同周期T）。k=0时，（1）式中对应的这一项称为直流分量，也就是 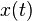$x(t)$ 在整个周期的平均值。 $k=\pm 1$ 时具有基波频率 $\omega_0=\frac{2\pi}{T}$ ，称为一次谐波或基波，类似的有二次谐波，三次谐波等等。

傅里叶级数的收敛性

至今还没有判断傅里叶级数的收敛性充分必要条件，但是对于实际问题中出现的函数，有很多种判别条件可用于判断收敛性。比如x(t)的可微性或级数的一致收敛性。在闭区间上满足狄利赫里条件的函数表示成的傅里叶级数都收敛。狄利赫里条件如下：

在定义区间上，x(t)须绝对可积；
在任一有限区间中，x(t)只能取有限个极值点；
在任何有限区间上，x(t)只能有有限个第一类间断点。

事实上，傅立叶级数在第一类间断点上收敛于初始函数左右极限的算术平均值。

1966年，里纳特·卡尔松证明了勒贝格二次可积函数的傅立叶级数一定是几乎处处收敛的，即级数在除了一个可数点集外均收敛。

吉布斯现象：在x(t)的不可导点上，如果我们只取(1)式右边的无穷级数中的有限项作和X(t)，那么X(t)在这些点上会有起伏。一个简单的例子是方波信号。

三角函数族的正交性

所谓的两个不同向量正交是指它们的内积为0，这也就意味着这两个向量之间没有任何相关性,例如，在三维欧氏空间中，互相垂直的向量之间是正交的。事实上，正交是垂直在数学上的的一种抽象化和一般化。一组n个互相正交的向量必然是线性无关的，所以必然可以张成一个n维空间，也就是说，空间中的任何一个向量可以用它们来线性表出。三角函数族的正交性用公式表示出来就是：

$\int _{0}^{2\pi}\sin (nx)\cos (mx) \,dx=0;$