二叉树的操作

树是一种重要的非线性数据结构，是以分枝关系定义的层次结构

 

基本术语：

 

 

树的遍历：指对树中所有结点的系统的访问，即依次对树中每个结点访问一次且仅访问一次！

                                           

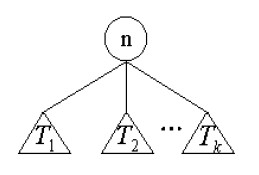
树的三种遍历方式：

1.前序遍历——先访问树根n，然后依次前序遍历T1,T2，……，Tk。

2.中序遍历——先中序遍历T1,然后访问树根n，接着依次对T2,T3,……，Tk进行中序遍历。

3.后续遍历——先依次对T1,T2,……,Tk,进行后续遍历，最后访问树根n

                

                             

树的存储结构：

1.父节点数组表示法

2.孩子表示法（链表表示法）

3.左儿子右儿子表示法

 

 

                                                                      

                                        

                                        二叉树(重要)

二叉树特点：

1. 每个结点至多有二棵子树（即不存在度大于2的结点）

2. 二叉树有左、右之分，且其次序不能随意颠倒

 

二叉树和树有许多相似之处，但二叉树不是树的特殊情形

基本形态：

 

 

具有3个结点的不同形态的二叉树：

 

二叉树的性质：

　    (1) 在二叉树中，第i层的结点总数不超过2^(i-1)；

　　(2) 深度为h的二叉树最多有2^h-1个结点(h>=1)，最少有h个结点；

 

　　(3) 对于任意一棵二叉树，如果其叶结点数为N0，而度数为2的结点总数为N2，

　　则N0=N2+1；（重要性质）

 

　　(4) 具有n个结点的完全二叉树的深度为int（log2n）+1

　　(5)有N个结点的完全二叉树各结点如果用顺序方式存储，则结点之间有如下关系：

　　若I为结点编号则 如果I<>1，则其父结点的编号为I/2；

　　如果2*I<=N，则其左儿子（即左子树的根结点）的编号为2*I；若2*I>N，则无左儿子；

　　如果2*I+1<=N，则其右儿子的结点编号为2*I+1；若2*I+1>N，则无右儿子。

　　(6)给定N个节点，能构成h(N)种不同的二叉树。

　　h(N)为卡特兰数的第N项。h(n)=C(n,2*n)/(n+1)。

 

 

 

几种特殊形态的二叉树：

1.满二叉树

2.完全二叉树(近似满二叉树)

 

在满二叉树中，从最右边结点开始连续往左删去若干个结点后得到的是一棵近似满二叉树

在完全二叉树中，若某个结点没有左儿子，则它一定没有右儿子，即该结点一定是一个叶结点

 

 

 

 

                                                   ADT二叉树的实现

虽然二叉树与树很相似，但它却不是树的特殊情形。

1.二叉树的顺序存储结构（一种无边表示）

2.二叉树的节点度表示法

 

3.用指针实现二叉树（重点）

#include<iostream>using namespace std;//二叉树节点结构定义为：class btnode{public:char data; //数据域btnode *lchild;        // 左子树btnode *rchild;       // 右子树};//补充：//三叉树定义（增加一个指向双亲结点的指针，以方便寻在双亲结点,但增加了存储空间的开销）//对于一般二叉树在不需要频繁查找双亲结点时通常采用二叉链表存储结构class tbtnode{public:char data;tbtnode *lchild;tbtnode *rchild;tbtnode *parent;   // 指向双亲结点的指针};/*二叉树的遍历就是将二叉树非线性关系的各个结点转化成一个线性的序列来访问。这里，访问的含义比较广泛。访问可以是查看结点的属性、更新结点数据值、增加或删除结点等。在这里以输出结点值为例研究二叉树的遍历如何进行。*///  =====          前序遍历(先序遍历)    =======/*先复习一下：前序遍历：指首先访问根结点，然后再前序遍历左子树，最后再前序遍历右子树。即在遍历左、右子树时仍然先访问根结点，然后遍历左子树，最后遍历右子树。因此，前序遍历二叉树是一个递归的过程。二叉树前序遍历的递归定义为：若二叉树为空，则空操作；否则，进行如下操作：1.访问根结点2.前序遍历左子树3.前序遍历右子树*/void PreOrder(btnode *bt) {if(bt != NULL){cout<<bt->data<<endl;   // 首先访问根结点PreOrder(bt->lchild);   // 然后递归前序遍历左子树PreOrder(bt->rchild);   // 最后递归前序遍历右子树}}// =======      中序遍历    =======/*中序遍历：指首先遍历左子树，然后访问根结点，最后遍历右子树。 即在遍历左、右子树时，仍然先遍历左子树，然后访问根结点，最后遍历右子树。因此，中序遍历也是一个递归的过程。二叉树中序遍历的递归定义为：若二叉树为空，则空操作；否则，进行如下操作：1.中序遍历根结点的左子树2.访问根结点3.中序遍历根结点的右子树*/void InOrder(btnode *bt){if(bt != NULL){InOrder(bt->lchild);       // 首先递归中序遍历左子树cout<<bt->data<<endl;   // 然后访问根结点InOrder(bt->rchild);       // 最后递归中序遍历右子树}}// =======      后序遍历     ==========/*后序遍历：指首先遍历左子树，然后遍历右子树，最后访问根结点。即在遍历左、右子树时，仍然先遍历左子树、然后遍历右子树，最后访问根结点。所以后序遍历仍然是递归过程。二叉树后序遍历同样进行的递归定义为： 若二叉树为空，则空操作；否则，进行如下操作：1.后序遍历根结点的左子树2.后续遍历根结点的右子树3.访问根结点*/void PostOrder(btnode *bt){if(bt != NULL){PostOrder(bt->lchild);     //  后续递归遍历左子树PostOrder(bt->rchild);     //  后续递归遍历右子树cout<<bt->data<<endl;      //  访问根结点}}/*   ====  二叉树的建立  =====首先建立二叉树的根结点，然后简历左子树，再建立右子树。这恰好符合前序遍历的思想，只不过将访问节点换成生成节点即可因为在含有n个结点的二叉树链表中一定有n+1个空指针域，所以在输入数据时一定要给出n+1个空指针值。一般以“-1”或“#”代替空指针。*/btnode* CreateBtree(){btnode *bt;char x;cin>>x;if(x == '#')bt = NULL;else{bt = new btnode;bt->data = x;bt->lchild = CreateBtree();bt->rchild = CreateBtree();}return bt;}/*  ===== 统计二叉树中叶子节点的个数 ====      若用二叉链表表示二叉树，其中左、右子树均为空的节点就是叶子节点，  可按先序遍历计算二叉树中的叶子节点个数n*/int Leaf(btnode *bt,int n){if(bt != NULL){if(bt->lchild==NULL && bt->rchild==NULL){++n;}n = Leaf(bt->lchild,n);n = Leaf(bt->rchild,n);}return (n);} /*  ===== 计算二叉树的高度 =====  */// 二叉树的高度为二叉树中结点层次的最大值。若一棵二叉树为空，则其高度为0，// 否则其高度等于左子树和右子树的最大高度加1;int high(btnode *bt){int h,lh,rh;if(bt == NULL)h=0;else{lh = high(bt->lchild);rh = high(bt->rchild);h = lh>rh ? lh+1 : rh+1;}return (h);}int main(){btnode *root;root = CreateBtree();PreOrder(root);return 0;}

原创 http://blog.csdn.net/shuangde800 ， By   D_Double