范围搜索 (Range Query)
来源:互联网 发布:端口出现感叹号 编辑:程序博客网 时间:2024/05/17 07:34
范围搜索
Author: Subhash Suri
译者:Koala++ / 屈伟
引
前一阵把搜索引擎的RangeQuery的逻辑重新写了一遍,我写的时候就感觉很不对劲,我们的搜索引擎采用的是一种非常怪异的实现,至少我没在别的搜索引擎里见过,或是在资料中看到过。我要解决的是二维坐标查询,比如你想知道你周围五公里内的医院在什么地方,蛮力解决方法就是把所有医院坐标得到,把x坐标循环过滤一遍,再把y坐标循环过滤一遍。其实这还好,因为一个城市一共也没多少医院,但如果调用方把坐标查询写前面,也就是先过滤x和y坐标,再过滤医院,那就悲剧了。
简单点的办法就是把x和y坐标有序地保存,那用二分查找定位到x-2.5km, x+2.5km, y-2.5km, y+2.5km,然后取x-2.5km到x+2.5km的posting list和y-2.5km到y+2.5km的posting list做and操作就可以了。
但是还能不能再快呢?这个问题我想了想也没什么头绪,偶然发现了RTree这个数据结构,我感觉这才是正道。
下面是Range Searching的翻译。原文地址:http://www.cs.ucsb.edu/~suri/cs235/RangeSearching.pdf
Range Search
我们这里讨论Range Search是希望能找到一个好的数据结构,它能高效地对对象(点,矩形,多边形)的集合进行范围查询。

我们要做的是根据对象的类型和查询的类型,来寻找一个能在多种应用场景下使用的基本数据结构。
时间-空间的平衡:我们在预处理和存储上耗费地越多,那我们就可以更快地完成一次查询。
这里主要考虑使用(近似)线性空间的数据结构。
Orthogonal Range Search
对于一个有n个点的集合P。它有2n个子集。对于一个几何的查询,它会有多少个可能的结果呢?

效率能提高的原因是在查询结果中只会有子集中的一部分。
正交范围搜索只处理与坐标轴平行的矩形空间中的点集合。(译注,也就是不能用查询像圆形,五角形这样的范围)。
接下来,我们先讨论一维空间中的排序和搜索问题,然后将一维空间的数据结构推广到多维空间。
1-Dimensional Search
令一维空间的点集合为P={p1, p2, ...,pn}。
查询是一个区间:

如果这个区间包含k个点,我们想在时间复杂度为O(log n + k)的情况下解决这个问题。
Hashing可以做到吗?为什么不能?(译注:Hash的查询时间复杂度为O(1+a),a是负载因子,hash在查询时只能依次查找,它的时间复杂度是O(n+an))。
一个排序后的数组可以得到这个时间复杂度边界,但是它无法推广到多维空间。
我们采用一种替代方案,用一个二叉平衡树。
Tree Search
在一个排序后的点(key)数组上建立一个平衡二叉树。
叶子结点对应的是点,中间结点是分支结点。
给定一个区间[xl0,xhi],在树上搜索xl0和xhi。
搜索得到的两个叶子结点中的叶子结点就是搜索的结果。
树搜索部分的时间复杂度是2log n,将叶子结点放入结果集的时间复杂度为O(k),这里假设叶子结点是被链在一起的。
Canonical subsets
S1, S1... Sk是Canonical子集,Si属于P。如果范围查询的结果可以写成几个Si的并集。(译注:canonical子集的解释http://en.wikipedia.org/wiki/Canonical,不必深究,就认为是子集就行了)。
Canonical子集有可能会重叠。
键(Key)是用来确定正确的Si,和高效地确定对于一个给定的查询,使用哪个Si。
在一维空间问题上,树中每一个结点都有一个Canonical子集:Sv是以v的根结点的子树的Canonical子集,它其中的元素是这个子树所有根结点中的点。

1D Range Query

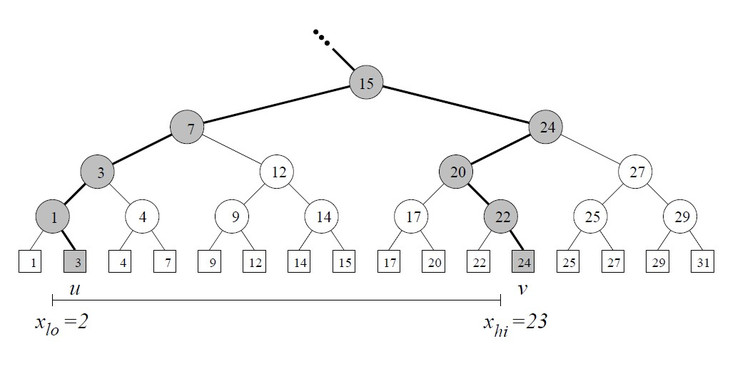
给定查询[xl0,xhi],查询树中满足u>= xl0的最左叶子结点,和满足v>= xhi的最左叶子结点。
所有在u和v之间的叶子结点都在所查询范围之内。
如果u= xl0或是v= xhi,那么u, v的canonical子集也包含在范围中。
将[u,v)区间范围内的所有其它点由区间中的最大子树决定。(译注:阴影中的子树)。
Query Processing
令z为从root到u,v搜索路径上的最后一个普通结点。
先看从z到u的最左边路径,当路径向左时,将右子树的canonical子集加入结果集。
从z到v的右边路径中,当路径向右时,将左子树的canonical子集加入结果集。

Analysis

因为搜索路径有O(log n)个结点,故有O(log n)个canonical子集,所以可以在O(log n)时间内找到。
得到结果集合,可以在线性时间内遍历这些子树,时间复杂度为O(k)。
如果只需要得到范围内点的数量,可以在每个结点中记录canonical集合的元素个数。
数据结构的空间复杂度为O(n),它查询一个范围的时间复杂度为O(log n)。
Multi-Dimensional Data
如何在高维空间中进行范围搜索?

kD-tree [Jon Bertley 1975]。它是k-dimensional tree的缩写。
它适用于一般的任意维空间。渐近搜索复杂度不是很好。
通过在x-y坐标上分裂这种方式来推广一维的树。在k维空间中,将会循环所有维坐标。
KD-Trees

一个二叉树,每个结点有两个值,所分裂的维,和分裂的值。
如果分裂在x坐标的s处,那么左子树的点都有x坐标<=s,右子树的点都有x坐标>s。对y坐标也是一样。
当只有O(1)个点剩余时,将它们放到一个叶子结点。
只有叶子结点中有点位置的信息,非叶子结点只用于分裂。
Splitting
为得到一个平衡树,使用坐标中位数来分裂——中位数本身放到左子树或是右子树都可以。
使用中位数分裂,可以保证树的高度为O(log n)。
分裂可以使用循环所有维的方式,或是根据数据做出选择,比如,可以选择数据分布最广的维。
Space Partitioning View
kD-tree是对空间的划分,每个结点都会引入对x轴或是y轴的划分。
点被划分成两部分,这两部分分别是左子树和右子树。
这些划分由矩形区域组成,称为单元(cell)(可能是没有边界的)。
根对应的是整个空间,随后每个子结点都只继承一半的空间。
叶子对应的是终止单元。
它是二分空间(Binary space Partitioning)的一种特殊情况。
construction
它可以以递归方式在O(n log n)时间内建成。
预先对x坐标和y坐标排序,并将两个排序数组交叉链接起来。(译注,即将每个点的x,y坐标链接起来)。
比如,可以通过扫描x数组得到x坐标的中位数,将数组分成两部分。再用交叉链接将y数组在O(n)时间复杂度内分成两部分。
现在有两个子问题,每个都有n/2的大小,并且它们都有自己的排序数据。递归。
递归式为T(n)=2T(n/2) + n,故它的时间复杂度为T(n) = O(n log n)。(译注,可以参考算法导论4.3节的主方法)。
Searching kD-Trees
设查询矩形为R。从根结点开始查找。
假设当前分裂的线是垂直的(也可以是水平的)。令v,w分别是左子结点和右子结点。
如果v是一个叶子结点,返回cell(v)交R,如果cell(v)属于R,返回cell(v)中所有点,如果cell(v)交R为空集,跳过。
对w进行相同的处理。
查询过程明显是没有问题的。那么它的时间复杂度是什么呢?
Search complexity
当cell(v)属于R,时间复杂度与cell(v)的大小成线性关系。
结点v访问的结点个数满足由cell(v)与R交集边界的限定。
如果cell(v)在R区域之外,我们就不用去查找它,如果cell(v)在R之内,我们就要枚举v中的所有点。只有在cell(v)与R局部重叠时才会去递归调用。kD-Tree的高度是O(log n)。
令l为穿过R的一条直线。
有多少个单元会与这条线相交?
因为分裂的维是从两个维中选择一个,所以思考的关键在于每次将树的两层一起考虑。
假设第一次划分是垂直的,第二次是水平的,我们就有四个单元,每一个有n/4个点。
一条直接只与两个单元相交。单元或是在R区域之内或是R区域之外。
递归式为:

从递归式可以得到时间复杂度为:Q(n)=O(n1/2)。
kD-Tree是一个有O(n)空间复杂度的数据结构,它可以在最坏时间O(n1/2+m)内完成二维空间范围查找,其中m是输出的大小。
d-Dim Search Complexity
更高维的时间复杂度是什么呢?
先尝试三维情况,再推广。
递归式是:
Q(n)=2d-1Q(n/2d)+1
从它推出时间复杂度:
Q(n)=O(n1-1/d)
kD-Tree是一个有(nd)空间复杂度的数据结构,它在d维空间中查找范围的最坏时间复杂度为O(n1-1/d+m),其中m是输出的大小。
Orthogonal Range Trees

将一维查找树推广到d维空间。
每次查找都会递归地分解到多个低维空间中去查找。
查找时间复杂度为O((log n)d+k),其中k是结果集大小。
时间和空间复杂度是O(n(log n)d-1)。
分散层叠(fractional cascading)从查找时间中消除了一个log n因子。
我们着眼于二维情况,但是它的思想是可以扩展到多维空间的。
2D Range Tree
令二维空间中的一个点集合为P={p1, p2, ...,pn}。
一个查询的一般形式为:R=[xlo,xhi]*[ylo,yhi]。
我们开始不考虑y坐标,在P上建立一个一维的x区域树。

在[xlo,xhi]区间的点集属于O(log n)个canonical集合。
这是一个结果的超集。它明显比|R交P|要大,所以我们不能采用依次查看每个点在不在canonical集合中这种耗时的方式。
Level 2 Trees
思想的核心是取得每个canonical集合的点,并在它们上面建立y区域树。
比如,canonical集合{9,12,14,15},用它的y坐标建立了一个新的区域树。

我们查找每个O(log n) canonical集合需要查找x区域树中的[xlo,xhi]范围和用它们的y区域树查找[ylo,yhi]范围。
y区域的查找中得到R交P这个结果集。
Canonical Sets
analysis
二维的查找时间复杂度为O((log n)2)。
1. 查找O(log n)个canonical集合。
2. 每个集合进行y范围查找需要O(log n)时间复杂性。

空间复杂度为O(n log n)。
1. x区域树中cononical集合的总大小是多少?
2. 非叶子结点个数=叶子结点个数。
3. 有一个大小为n的集合,二个大小为n/2的集合,以此类推。
4. 总共是O(n log n)。
5. 每个大小为m的canonical集合需要O(m)的空间来存储y区域树。
6. 所以,总的空间复杂度是O(n log n)。
construction

x区域树可以在O(n log n)时间内建立。
初看起来,因为y树的总大小是O(n log n),所以它需要O(n(log n)2)的时间来建立。
但是通过自底向上建立它们,我们可以避免在每个结点上的排序时间。
一旦子结点的y区域树建立了,我们就可以将它们的y数组在线性时间内合并。
建立一维区域树在排序后的时间复杂度是线性的。
所以,总的时间复杂度是O(n log n),是所有y区域树的总大小。
d-Dim Range Trees
多级区域树的思想可以很自然地扩展到任意d维。
在第一维上建立一个x区域树。
在树中每个结点v上,在v结点的cononical集合上为剩余的(d-1)维建立一个(d-1)维的区域树。
查找时间复杂度每一维增加log n因子——每一维都会增加canonical集合总大小log n倍。
所以查找时间为O((log n)d)。
建树的空间和时间复杂度是O(n(log n)d-1)。

- 范围搜索 (Range Query)
- 范围搜索 (Range Query)
- 范围搜索 (Range Query)
- 范围搜索 (Range Query)
- Lucene的数字范围搜索 (Numeric Range Query)原理
- Lucene的数字范围搜索 (Numeric Range Query)原理
- 如何在Lucene里面进行数字范围搜索 (Numeric Range Query)
- Lucene2.9 范围查询Range Query
- 范围最小值问题 (Range Minimum Query,RMQ)
- 范围最小值查询 RMQ (Range Minimum Query)
- Geeks - Range Minimum Query RMQ范围最小值查询
- 范围最小值问题(Range Minimum Query,RMQ)
- LeetCode 34 Search for a Range(搜索范围)
- LeetCode 34. Search for a Range(搜索范围)
- LeetCode 303 Range Sum Query - Immutable(范围总和查询-永久不变)(*)
- LeetCode 307 Range Sum Query - Mutable(范围和查询-可变)
- LeetCode 304 Range Sum Query 2D - Immutable(范围求和2D - 不可变)
- lintcode--平面范围求和-不可变矩阵(leetcode--Range Sum Query 2D)
- Android Service被关闭后自动重启,解决被异常kill 服务
- [iOS]深入浅出ObjC之消息
- [Python] 找寻A文件中有而B文件中没有的记录
- 贪心算法 - 哈夫曼编码 Huffman
- 带环的链表
- 范围搜索 (Range Query)
- 黑马程序员_SQL总结一
- Problems occurred when invoking code from plug-in: "org.eclipse.jface".
- common test 记录
- 20120808 (X)HTML与CSS核心基础
- c# webbroswer 中文乱码
- CALayer
- Android应用开发提高系列(4)——Android动态加载(上)——加载未安装APK中的类
- struts2 set标签








