First-countable space and Second-countable space

来源：互联网发布：什么网络电视盒子最好编辑：程序博客网时间：2024/06/14 02:04

转自：http://en.wikipedia.org/wiki/First-countable_space

First-countable space

In topology, a branch of mathematics, a first-countable space is a topological space satisfying the "first axiom of countability". Specifically, a space X is said to be first-countable if each point has a countable neighbourhood basis (local base). That is, for each point x in X there exists a sequence U₁, U₂, … of open neighbourhoods of x such that for any open neighbourhood V of x there exists an integer i with U_i contained in V.

转自：http://en.wikipedia.org/wiki/Second-countable_space

Second-countable space

In topology, a second-countable space, also called a completely separable space, is a topological space satisfying the second axiom of countability. A space is said to be second-countable if its topology has a countable base. More explicitly, this means that a topological space 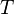$T$ is second countable if there exists some countable collection 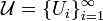$\mathcal{U} = \{U_i\}_{i=1}^\infty$ of open subsets of 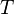$T$ such that any open subset of 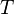$T$ can be written as a union of elements of some subfamily of 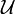$\mathcal{U}$ . Like other countability axioms, the property of being second-countable restricts the number of open sets that a space can have.

Most "well-behaved" spaces in mathematics are second-countable. For example, Euclidean space (Rⁿ) with its usual topology is second-countable. Although the usual base of open balls is not countable, one can restrict to the set of all open balls with rational radii and whose centers have rational coordinates. This restricted set is countable and still forms a basis.