hdu_1.3.1_FatMouse' Trade,hdu_1.3.2_Tian Ji -- The Horse Racing

                        FatMouse' Trade

Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others)

Total Submission(s): 3187 Accepted Submission(s): 971

 

Problem Description

FatMouse prepared M pounds of cat food, ready to trade with the cats guarding the warehouse containing his favorite food, JavaBean.
The warehouse has N rooms. The i-th room contains J[i] pounds of JavaBeans and requires F[i] pounds of cat food. FatMouse does not have to trade for all the JavaBeans in the room, instead, he may get J[i]* a% pounds of JavaBeans if he pays F[i]* a% pounds of cat food. Here a is a real number. Now he is assigning this homework to you: tell him the maximum amount of JavaBeans he can obtain.

 

 

Input

The input consists of multiple test cases. Each test case begins with a line containing two non-negative integers M and N. Then N lines follow, each contains two non-negative integers J[i] and F[i] respectively. The last test case is followed by two -1's. All integers are not greater than 1000.

 

 

Output

For each test case, print in a single line a real number accurate up to 3 decimal places, which is the maximum amount of JavaBeans that FatMouse can obtain.

 

 

Sample Input

5 37 24 35 220 325 1824 1515 10-1 -1

 

 

Sample Output

13.33331.500

 

 

Author

CHEN, Yue

 

 

Source

ZJCPC2004

 

 

Recommend

JGShining

 

代码：

#include<iostream>#include<vector>#include<queue>#include<stack>#include<stdio.h>#include<algorithm>#include<cstdio>#include<string>#include<cstring>using namespace std;//头文件struct Num{double J;double F;    double a;};bool cmp(Num x,Num y){return x.a>y.a;}int main(){double jb;int cas;double sum;Num shuzhu[1000];cout.precision(3);while(cin>>jb>>cas){if(jb==-1&&cas==-1)break;sum=0;for(int i=0;i<cas;i++){cin>>shuzhu[i].J>>shuzhu[i].F;shuzhu[i].a=shuzhu[i].J/shuzhu[i].F;}sort(shuzhu,shuzhu+cas,cmp);for(int i=0;i<cas;i++){    if(jb>=shuzhu[i].F)    {    sum+=shuzhu[i].J;    jb-=shuzhu[i].F;    }    else    {    sum+=shuzhu[i].a*jb;    break;    }}cout<<fixed<<sum<<endl;}return 0;} 

 

Tian Ji -- The Horse Racing

Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others)Total Submission(s): 2774 Accepted Submission(s): 696 

Problem Description

Here is a famous story in Chinese history.

"That was about 2300 years ago. General Tian Ji was a high official in the country Qi. He likes to play horse racing with the king and others."

"Both of Tian and the king have three horses in different classes, namely, regular, plus, and super. The rule is to have three rounds in a match; each of the horses must be used in one round. The winner of a single round takes two hundred silver dollars from the loser."

"Being the most powerful man in the country, the king has so nice horses that in each class his horse is better than Tian's. As a result, each time the king takes six hundred silver dollars from Tian."

"Tian Ji was not happy about that, until he met Sun Bin, one of the most famous generals in Chinese history. Using a little trick due to Sun, Tian Ji brought home two hundred silver dollars and such a grace in the next match."

"It was a rather simple trick. Using his regular class horse race against the super class from the king, they will certainly lose that round. But then his plus beat the king's regular, and his super beat the king's plus. What a simple trick. And how do you think of Tian Ji, the high ranked official in China?"



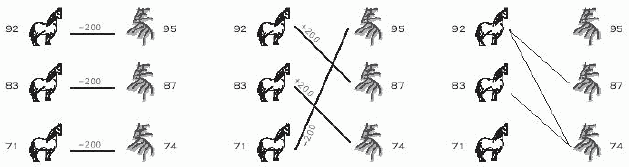
Were Tian Ji lives in nowadays, he will certainly laugh at himself. Even more, were he sitting in the ACM contest right now, he may discover that the horse racing problem can be simply viewed as finding the maximum matching in a bipartite graph. Draw Tian's horses on one side, and the king's horses on the other. Whenever one of Tian's horses can beat one from the king, we draw an edge between them, meaning we wish to establish this pair. Then, the problem of winning as many rounds as possible is just to find the maximum matching in this graph. If there are ties, the problem becomes more complicated, he needs to assign weights 0, 1, or -1 to all the possible edges, and find a maximum weighted perfect matching...

However, the horse racing problem is a very special case of bipartite matching. The graph is decided by the speed of the horses --- a vertex of higher speed always beat a vertex of lower speed. In this case, the weighted bipartite matching algorithm is a too advanced tool to deal with the problem.

In this problem, you are asked to write a program to solve this special case of matching problem.

Input

The input consists of up to 50 test cases. Each case starts with a positive integer n (n <= 1000) on the first line, which is the number of horses on each side. The next n integers on the second line are the speeds of Tian’s horses. Then the next n integers on the third line are the speeds of the king’s horses. The input ends with a line that has a single 0 after the last test case.

Output

For each input case, output a line containing a single number, which is the maximum money Tian Ji will get, in silver dollars.

Sample Input

392 83 7195 87 74220 2020 20220 1922 180

Sample Output

20000

 

Source

2004 Asia Regional Shanghai

Recommend

JGShining

 

 代码：

#include<iostream>#include<vector>#include<queue>#include<stack>#include<stdio.h>#include<algorithm>#include<cstdio>#include<string>#include<cstring>using namespace std;//头文件bool cmp(int a,int b){return a>b;}int main(){int n;int ti,tj,qi,qj;int tianji[10000];int qiwang[10000];while(cin>>n,n){if(n==0) break;for(int i=0;i<n;i++)cin>>tianji[i];for(int i=0;i<n;i++)cin>>qiwang[i];sort(tianji,tianji+n,cmp);sort(qiwang,qiwang+n,cmp); ti=qi=0; tj=qj=n-1; int ying=0; for(int i=0;i<n;i++) { if(tianji[ti]>qiwang[qi]) { ti++; qi++; ying++; } else if(tianji[ti]<qiwang[qi]) { tj--; qi++; ying--; } else { if(tianji[tj]>qiwang[qj]) { tj--; qj--; ying++;  } else if(tianji[tj]>qiwang[qj]) { tj--; qi++; ying--; } else{ if(tianji[tj]<qiwang[qi]) { tj--;     qi++;     ying--; } } } } cout<<ying*200<<endl;}return 0;}//贪心策略 开始的时候没有注意到最后如果最快和最慢的马都一样的时候 应该田忌的最慢的马和齐王最快的马相比较