POJ 1273 最大流问题

POJ http://poj.org/problem?id=1273 最大流问题；参考 http://www.cnblogs.com/kuangbin/archive/2011/07/26/2117636.html

1. 通过bfs广搜的方法寻找增广路径。

    注意，广搜一定可以找到流量至少为1的增广路径，否则，残余网络中不存在增广路。

2. 对bfs找到的增广路，减掉相应的流量，并增加相应的反向流量（反向边）。

 重复1和2的过程，不存在增广路则算法结束。

#include<stdio.h>#include<queue>#define INF 0x7FFFFFFF;using namespace std;const int N=201;int n,m; int s,e;// we assum that the start point is 1;int max_flow=0;int map[N][N],path[N],flow[N];int bfs(){queue<int> q;q.push(s);memset(path,0,sizeof(path));path[s]=-1;flow[s]=INF;while(!q.empty()){int t=q.front();q.pop();if(t==e) break;for(int i=1;i<=m;i++){if(map[t][i]!=0&&path[i]==0){flow[i]=flow[t]>map[t][i]?map[t][i]:flow[t];path[i]=t;q.push(i);}}}if(path[e]==0) return -1;    return flow[e];}void Ford_Fulkerson(){while(true){int flow_up=bfs();if(flow_up==-1) break;else{max_flow+=flow_up;int p=e;while(p!=s){map[path[p]][p]-=flow_up;map[p][path[p]]+=flow_up;p=path[p];}}}}int main(){while(scanf("%d %d",&n,&m)!=EOF){max_flow=0;s=1;e=m;memset(map,0,sizeof(map));while(n--){int a,b,c;scanf("%d %d %d",&a,&b,&c);map[a][b]+=c;}Ford_Fulkerson();printf("%d\n",max_flow);}return 1;}    

基于邻接表存储的代码如下，这里对重边的处理是：只增加节点；但bfs()扫描所有的邻接节点，如果weight！=0认为存在该边；

#include<stdio.h>#include<queue>#define INF 0x7FFFFFFF;using namespace std;const int N=201;int n,m; int s,e;// we assum that the start point is 1;int max_gain;struct node{int end_label;int weight;node *next;node():next(NULL){}node(int a,int b,node *p){end_label=a;weight=b;next=p;}};node* G[N];int path[N],flow[N];int bfs(){queue<int> q;q.push(s);memset(path,0,sizeof(path));path[s]=-1;flow[s]=INF;while(!q.empty()){int t=q.front();q.pop();if(t==e) break;node* p=G[t];while(p!=NULL){int l=p->end_label;if(path[l]==0&&p->weight!=0){flow[l]=flow[t]>p->weight?p->weight:flow[t];path[l]=t;q.push(l);}p=p->next;}}if(path[e]==0) return -1;    return flow[e];}void Ford_Fulkerson(){while(true){int flow_up=bfs();if(flow_up==-1) break;else{max_gain+=flow_up;int l=e;while(l!=s){node *p;for(p=G[l];p!=NULL;p=p->next)if(p->end_label==path[l]) break;if(p!=NULL)p->weight+=flow_up;elseG[l]=new node(path[l],flow[l],G[l]);for(p=G[path[l]];p!=NULL;p=p->next)if(p->end_label==l) break;p->weight-=flow_up;l=path[l];}}}}int main(){while(scanf("%d %d",&n,&m)!=EOF){max_gain=0;s=1;e=m;memset(G,NULL,sizeof(G));while(n--){int a,b,c;scanf("%d %d %d",&a,&b,&c);int flag=1;for(node *p=G[a];p!=NULL;p=p->next)if(p->end_label==b){flag=0;p->weight+=c;}if(flag)G[a]=new node(b,c,G[a]);}Ford_Fulkerson();printf("%d\n",max_gain);}//释放内存，省略；return 1;}    

The Standard Maximum Flow Problem
So, what are we being asked for in a max-flow problem? The simplest form that the statement could take would be something along the lines of: "A list of pipes is given, with different flow-capacities. These pipes are connected at their endpoints. What is the maximum amount of water that you can route from a given starting point to a given ending point?" or equivalently "A company owns a factory located in city X where products are manufactured that need to be transported to the distribution center in city Y. You are given the one-way roads that connect pairs of cities in the country, and the maximum number of trucks that can drive along each road. What is the maximum number of trucks that the company can send to the distribution center?" 

A first observation is that it makes no sense to send a truck to any other city than Y, so every truck that enters a city other than Y must also leave it. A second thing to notice is that, because of this, the number of trucks leaving X is equal to the number of trucks arriving in Y. 

Rephrasing the statement in terms of graph theory, we are given a network - a directed graph, in which every edge has a certain capacity c associated with it, a starting vertex (the source, X in the example above), and an ending vertex (the sink). We are asked to associate another value f satisfying f ≤ c for each edge such that for every vertex other than the source and the sink, the sum of the values associated to the edges that enter it must equal the sum of the values associated to the edges that leave it. We will call f the flow along that edge. Furthermore, we are asked to maximize the sum of the values associated to the arcs leaving the source, which is the total flow in the network. 

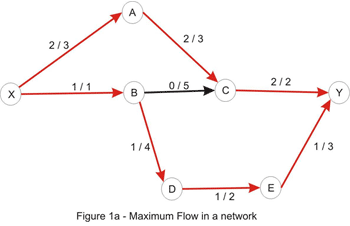
The image below shows the optimal solution to an instance of this problem, each edge being labeled with the values f/c associated to it. 

How to Solve It
Now how do we actually solve the problem? First, let us define two basic concepts for understanding flow networks: residual networks and augmenting paths. Consider an arbitrary flow in a network. The residual network has the same vertices as the original network, and one or two edges for each edge in the original. More specifically, if the flow along the edge x-y is less than the capacity there is a forward edge x-y with a capacity equal to the difference between the capacity and the flow (this is called the residual capacity), and if the flow is positive there is a backward edge y-x with a capacity equal to the flow on x-y. An augmenting path is simply a path from the source to the sink in the residual network, whose purpose is to increase the flow in the original one. It is important to understand that the edges in this path can point the "wrong way" according to the original network. The path capacity of a path is the minimum capacity of an edge along that path. Let's take the following example: 

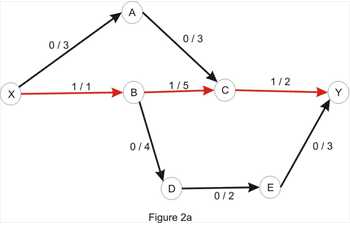
By considering the path X_A_C_Y, we can increase the flow by 1 - the edges X_A and A_C have capacity of 3, as in the original network, but the edge C_Y has capacity 1, and we take the minimum of these values to get the path capacity. Increasing the flow along this path with 1 yields the flow below: 

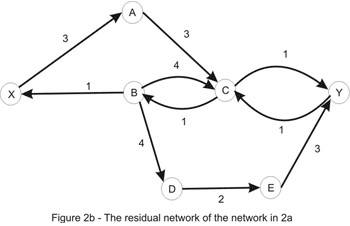
The value of the current flow is now 2, and as shown in Figure 1, we could do better. So, let's try to increase the flow. Clearly, there is no point in considering the directed paths X_A_C_Y or X_B_D_E_Y as the edges C_Y and X_B, respectively, are filled to capacity. As a matter of fact, there is no directed path in the network shown above, due to the edges mentioned above being filled to capacity. At this point, the question that naturally comes to mind is: is it possible to increase the flow in this case? And the answer is yes, it is. Let's take a look at the residual network: 

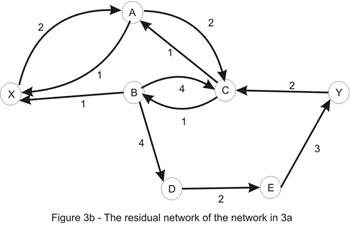
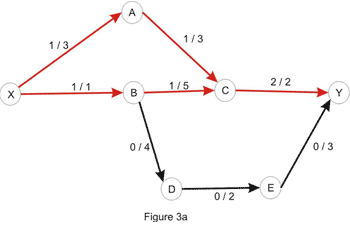
Let's consider the only path from X to Y here: X_A_C_B_D_E_Y. Note that this is not a path in the directed graph, because C_B is walked in the opposite way. We'll use this path in order to increase the total flow in the original network. We'll "push" flow on each of the edges, except for C_B which we will use in order to "cancel" flow on B_C. The amount by which this operation can be performed is limited by the capacities of all edges along the path (as shown in Figure 3b). Once again we take the minimum, to conclude that this path also has capacity 1. Updating the path in the way described here yields the flow shown in Figure 1a. We are left with the following residual network where a path between the source and the sink doesn't exist: 

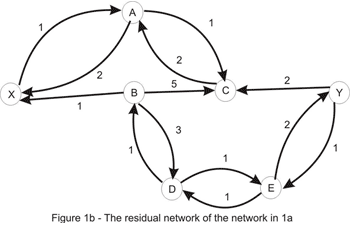
This example suggests the following algorithm: start with no flow everywhere and increase the total flow in the network while there is an augmenting path from the source to the sink with no full forward edges or empty backward edges - a path in the residual network. The algorithm (known as the Ford-Fulkerson method) is guaranteed to terminate: due to the capacities and flows of the edges being integers and the path-capacity being positive, at each step we get a new flow that is closer to the maximum. As a side note, the algorithm isn't guaranteed to even terminate if the capacities are irrationals. 

What about the correctness of this algorithm? It is obvious that in a network in which a maximum flow has been found there is no augmenting path, otherwise we would be able to increase the maximum value of the flow, contradicting our initial assumption. If the converse of this affirmation is true, so that when there is no augmenting path, the value of the flow has reached its maximum, we can breathe a sigh of relief, our algo is correct and computes the maximum flow in a network. This is known as the max-flow min-cut theorem and we shall justify its correctness in a few moments. 

A cut in a flow network is simply a partition of the vertices in two sets, let's call them A and B, in such a way that the source vertex is in A and the sink is in B. The capacity of a cut is the sum of the capacities of the edges that go from a vertex in A to a vertex in B. The flow of the cut is the difference of the flows that go from A to B (the sum of the flows along the edges that have the starting point in A and the ending point in B), respectively from B to A, which is exactly the value of the flow in the network, due to the entering flow equals leaving flow - property, which is true for every vertex other than the source and the sink. 

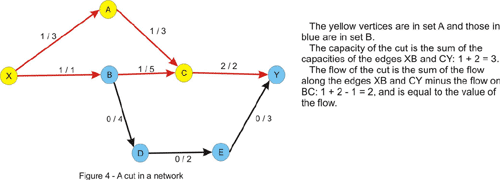
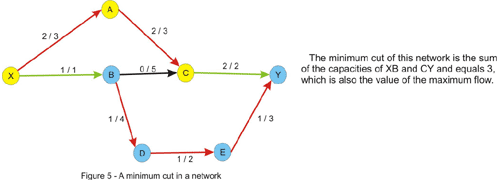
Notice that the flow of the cut is less or equal to the capacity of the cut due to the constraint of the flow being less or equal to the capacity of every edge. This implies that the maximum flow is less or equal to every cut of the network. This is where the max-flow min-cut theorem comes in and states that the value of the maximum flow through the network is exactly the value of the minimum cut of the network. Let's give an intuitive argument for this fact. We will assume that we are in the situation in which no augmenting path in the network has been found. Let's color in yellow, like in the figure above, every vertex that is reachable by a path that starts from the source and consists of non-full forward edges and of non-empty backward edges. Clearly the sink will be colored in blue, since there is no augmenting path from the source to the sink. Now take every edge that has a yellow starting point and a blue ending point. This edge will have the flow equal to the capacity, otherwise we could have added this edge to the path we had at that point and color the ending point in yellow. Note that if we remove these edges there will be no directed path from the source to the sink in the graph. Now consider every edge that has a blue starting point and a yellow ending point. The flow on this edge must be 0 since otherwise we could have added this edge as a backward edge on the current path and color the starting point in yellow. Thus, the value of the flow must equal the value of the cut, and since every flow is less or equal to every cut, this must be a maximum flow, and the cut is a minimum cut as well. 

In fact, we have solved another problem that at first glance would appear to have nothing to do with maximum flow in a network, ie. given a weighted directed graph, remove a minimum-weighted set of edges in such a way that a given node is unreachable from another given node. The result is, according to the max-flow min-cut theorem, the maximum flow in the graph, with capacities being the weights given. We are also able to find this set of edges in the way described above: we take every edge with the starting point marked as reachable in the last traversal of the graph and with an unmarked ending point. This edge is a member of the minimum cut.