算法网站:Undirected Graphs

Graphs.

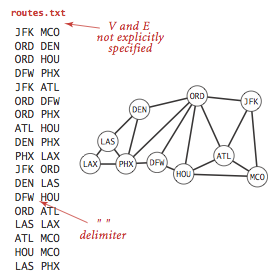
A graph is a set of vertices and a collectionof edges that each connect a pair of vertices.We use the names 0 through V-1 for the vertices in a V-vertex graph.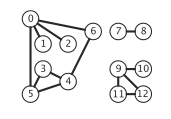

Glossary.

Here are some definitions that we use.

• A self-loop is an edge that connects a vertex toitself.
• Two edges are parallel if they connect the same pair ofvertices.
• When an edge connects two vertices, we say that the vertices areadjacent to one another and that the edge isincident on both vertices.
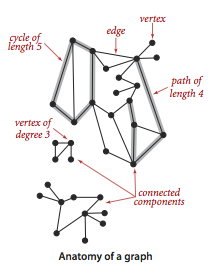
• The degree of a vertex is the number of edges incident on it.
• A subgraph is a subset of a graph's edges (and associatedvertices) that constitutes a graph.
• A path in a graph is a sequence of vertices connected by edges.A simple path is one with no repeated vertices.
• A cycle is a path (with at least one edge)whose first and last vertices are the same.Asimple cycle is a cycle with no repeated edges or vertices(except the requisite repetition of the first and last vertices).
• The length of a path or a cycle is its number of edges.
• We say that one vertex is connected to another if thereexists a path that contains both of them.
• A graph is connected if there is a path from every vertex toevery other vertex.
• A graph that is not connected consists of a set ofconnected components, which are maximal connected subgraphs.
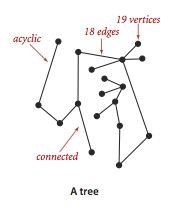
• An acyclic graph is a graph with no cycles.
• A tree is an acyclic connected graph.
• A forest is a disjoint set of trees.
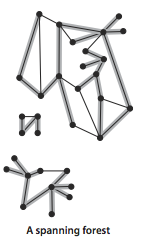
• A spanning tree of a connected graph is a subgraph thatcontains all of that graph's vertices and is a single tree.Aspanning forest of a graph is the union of the spanningtrees of its connected components.
• A bipartite graph is a graph whose vertices we can divideinto two sets such that all edges connect a vertex in one set with a vertexin the other set.

Undirected graph data type.

We implement the following undirected graph API.

The key method adj() allows client codeto iterate through the vertices adjacent to a givenvertex. Remarkably, we can build all of the algorithms that weconsider in this section on the basic abstraction embodied inadj().

We prepare the test data tinyG.txt,mediumG.txt, andlargeG.txt, using the followinginput file format.

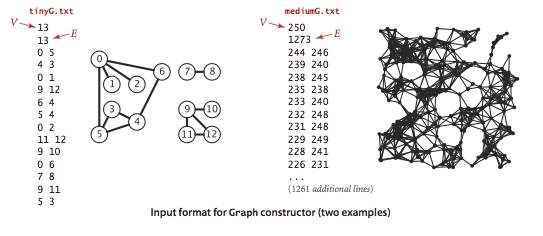
GraphClient.java containstypical graph-processing code.

Graph representation.

We use the adjacency-lists representation, where we maintaina vertex-indexed array of lists of the vertices connected by an edgeto each vertex.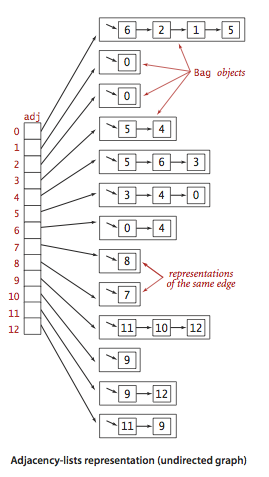

Graph.javaimplements the graph API using the adjacency-lists representation.AdjMatrixGraph.javaimplements the same API using the adjacency-matrix representation.

Depth-first search.

Depth-first search is a classic recursive method for systematicallyexamining each of the vertices and edges in a graph. To visit a vertex

• Mark it as having been visited.
• Visit (recursively) all the vertices that are adjacent to it andthat have not yet been marked.

DepthFirstSearch.javaimplements this approach and the following API:

Finding paths.

It is easy to modify depth-first search to not only determine whether thereexists a path between two given vertices but to find such a path (if one exists).We seek to implement the following API:

To accomplish this, we remember the edge v-w that takes us to eachvertexw for the first time by setting edgeTo[w]to v. In other words,v-w is the last edge on the knownpath from s to w. The result of the search is a tree rooted at the source;edgeTo[] is a parent-linkrepresentation of that tree. DepthFirstPaths.javaimplements this approach.

Breadth-first search.

Depth-first search finds some path from a source vertex s to a target vertex v.We are often interested in finding theshortest such path (one with a minimal number of edges). Breadth-first search is a classic method based on this goal.To find a shortest path froms to v,we start at s and check for v among all the vertices that we can reach by following one edge, then we check forvamong all the vertices that we can reach from s by following two edges, and so forth.

To implement this strategy, we maintain a queue of all vertices thathave been marked but whose adjacency lists have not been checked.We put the source vertex on the queue, then perform the followingsteps until the queue is empty:

• Remove the next vertex v from the queue.
• Put onto the queue all unmarked vertices that are adjacent to v and mark them.

BreadthFirstPaths.javais an implementation of thePaths API that finds shortest paths.It relies on Queue.java for the FIFO queue.

Connected components.

Our next direct application of depth-first search is to find the connected components of a graph.Recall from Section 1.5 that "is connected to" is an equivalence relationthat divides the vertices into equivalence classes (the connected components).For this task, we define the following API:

CC.javauses DFS to implement this API.

Proposition. DFS marks all the vertices connected to a given sourcein time proportional to the sum of their degrees and providesclients with a path from a given source to any marked vertex in time proportional to its length.

Proposition. For any vertex v reachable from s,BFS computes a shortest path froms to v(no path from s to v has fewer edges).BFS takes time proportional to V + E in the worst case.

Proposition. DFS uses preprocessing time and space proportionalto V + E to support constant-time connectivity queries in a graph.

More depth-first search applications.

The problems that we have solved with DFS are fundamental.Depth-first search can also be used to solve the following problems:

• Cycle detection: Is a given graph acyclic?Cycle.java uses depth-first searchto determine whether a graph has a cycle, and if so return one.It takes time proportional to V + E in the worst case.
• Two-colorability: Can the vertices of a given graphbe assigned one of two colors in such a way that no edge connectsvertices of the same color?Bipartite.java uses depth-first searchto determine whether a graph has a bipartition; if so, return one;if not, return an odd-length cycle.It takes time proportional to V + E in the worst case.
• Bridge:A bridge (or cut-edge) is an edge whose deletion increases the number of connected components. Equivalently, an edge is a bridge if and only if it is not contained in any cycle.Bridge.javauses depth-first search to find time the bridges in a graph.It takes time proportional to V + E in the worst case.
• Biconnectivity:An articulation vertex (or cut vertex) is a vertexwhose removal increases the number of connected components.A graph isbiconnected if it has no articulation vertices.Biconnected.javauses depth-first search to find the bridges and articulation vertices.It takes time proportional to V + E in the worst case.
• Planarity:A graph is planar if it can be drawn in the plane such that no edgescross one another. The Hopcroft-Tarjan algorithm is an advanced application of depth-first search that determineswhether a graph is planar in linear time.

Symbol graphs.

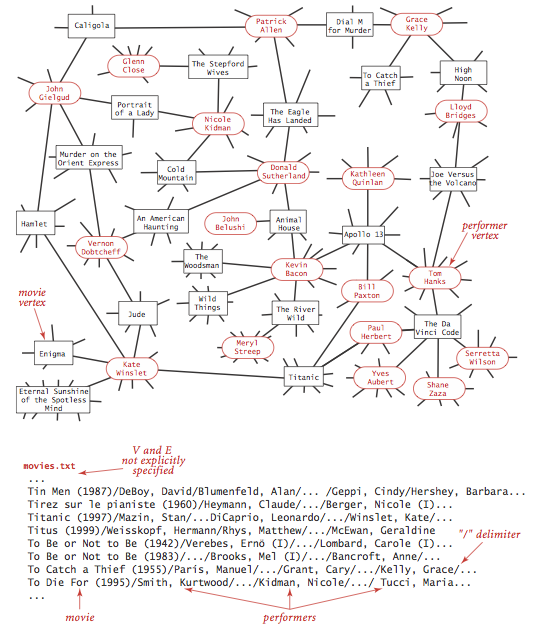
Typical applications involve processing graphs using strings, not integer indices, to define and refer to vertices.To accommodate such applications, we define an input format with the following properties:

• Vertex names are strings.
• A specified delimiter separates vertex names (to allow for the possibility ofspaces in names).
• Each line represents a set of edges, connecting the first vertexname on the line to each of the other vertices named on the line.

The input file routes.txt is a small example.

The input file movies.txt is a larger examplefrom the Internet Movie Database.This file consists of lines listing a movie name followed by a list of theperformers in the movie.

• API.The following API allows us to use our graph-processing routines for such input files.

  

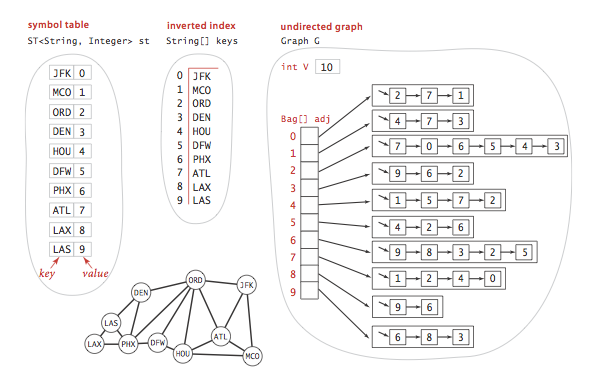
• Implementation.SymbolGraph.java implements the API.It builds three data structures:
  • A symbol table st with String keys (vertex names)and int values (indices)
  • An array keys[] that serves as an inverted index,giving the vertex name associated with each integer index
  • A Graph G built using the indices to refer to vertices

  

• Degrees of separation.DegreesOfSeparation.javauses breadth-first search to find the degree of separation betweentwo individuals in a social network. For the actor-movie graph, it plays the Kevin Bacon game.

Exercises

3. Create a copy constructor for Graph.javathat takes as input a graph G and creates and initializes a new copyof the graph. Any changes a client makes toG should not affect the newly created graph.
13. Add a distTo() method to BreadthFirstPaths.java,which returns the number of edges on the shortest path from thesource to a given vertex. AdistTo() query should run in constant time.
23. Write a program BaconHistogram.javathat prints a histogram of Kevin Bacon numbers, indicating how many performers frommovies.txt have a Bacon numberof 0, 1, 2, 3, ... . Include a category for those who have an infinite number (not connected to Kevin Bacon).
26. Write a SymbolGraph client DegreesOfSeparationDFS.javathat uses depth-first instead of breadth-first search to find paths connecting two performers.
27. Determine the amount of memory used by Graph to represent a graph withV vertices andE edges, using the memory-cost model of Section 1.4.

    Solution.56 + 40V + 128E.MemoryOfGraph.java computes it empiricallyassuming that noInteger values are cached—Javatypically caches the integers -128 to 127.

Creative Problems

32. Parallel edge detection.Devise a linear-time algorithm to count the parallel edges in a graph.

    Hint: maintain a boolean array of the neighbors of a vertex,and reuse this array by only reinitializing the entries as needed.

36. Two-edge connectivity.A bridge in a graph is an edge that,if removed, would separate a connected graph into two disjoint subgraphs.A graph that has no bridges is said to betwo-edge connected.Develop a DFS-based data type Bridge.javafor determining whether a given graph is edge connected.

Web Exercises

1. Find some interesting graphs. Are they directed or undirected?Sparse or dense?
2. Degree.The degree of a vertex is the number of incident edges. Add a methodint degree(int v) toGraph that returns thedegree of the vertex v.
3. Suppose you use a stack instead of a queue when running breadth-first search.Does it still compute shortest paths?
4. DFS with an explicit stack.Give an example of possibility of stack overflow with DFS using the function callstack, e.g., line graph.ModifyDepthFirstPaths.javaso that it uses an explicit stack instead of the function call stack.
5. Perfect maze.Generate a perfect maze like this one

   

   Write a program Maze.javathat takes a command line parameter N, and generates a randomN-by-N perfect maze.A maze isperfect if it has exactly one path between everypair of points in the maze, i.e., no inaccessible locations, nocycles, and no open spaces.Here's a nice algorithm to generate such mazes. Consider an N-by-N gridof cells, each of which initially has a wall between it and its fourneighboring cells. For each cell (x, y), maintain a variablenorth[x][y]that is true if there is wall separating (x, y) and (x, y + 1).We have analogous variableseast[x][y], south[x][y], andwest[x][y] for the corresponding walls. Note that if there isa wall to the north of (x, y) thennorth[x][y] = south[x][y+1] = true.Construct the maze by knocking down some of the walls as follows:

   1. Start at the lower level cell (1, 1).
   2. Find a neighbor at random that you haven't yet been to.
   3. If you find one, move there, knocking down the wall. If you don'tfind one, go back to the previous cell.
   4. Repeat steps ii. and iii. until you've been to every cell in the grid.

   Hint:maintain an (N+2)-by-(N+2) grid of cells to avoid tedious special cases.

6. Getting out of the maze.Given an N-by-N maze (like the one created in the previous exercise), write a program to find a path from the start cell (1, 1)to the finish cell (N, N), if it exists.To find a solution to the maze, run the following algorithm, startingfrom (1, 1) and stopping if we reach cell (N, N).

   explore(x, y)-------------  - Mark the current cell (x, y) as "visited."  - If no wall to north and unvisited, then explore(x, y+1).  - If no wall to east and  unvisited, then explore(x+1, y).  - If no wall to south and unvisited, then explore(x, y-1).  - If no wall to west and  unvisited, then explore(x-1, y).

7. Maze game. Develop a maze game like this one fromgamesolo.com,where you traverse a maze, collecting prizes.
8. Actor graph.An alternate (and perhaps more natural)way to compute Kevin Bacon numbers is to build a graph where each node is an actor. Two actors are connectedby an edge if they appear in a movie together. Calculate Kevin Baconnumbers by running BFS on the actor graph. Compare the running timeversus the algorithm described in the text. Explain why theapproach in the text is preferable.Answer: it avoids multiple parallel edges. As a result,it's faster and uses less memory. Moreover, it's more convenientsince you don't have to label the edges with the movie names - allnames get stored in the vertices.
9. Center of the Hollywood universe.We can measure how good of a center that Kevin Bacon is by computingtheirHollywood number. The Hollywood number of Kevin Baconis the average Bacon number of all the actors. The Hollywood numberof another actor is computed the same way, but we make them be thesource instead of Kevin Bacon. Compute Kevin Bacon's Hollywood numberand find an actor and actress with better Hollywood numbers.
10. Fringe of the Hollywood universe.Find the actor (who is connected to Kevin Bacon) that has the highestHollywood number.
11. Word ladders.Write a program WordLadder.javathat takes two 5 letter strings from the command line, and reads ina list of5 letter wordsfrom standard input, and prints out a shortestword ladderconnecting the two strings (if it exists).Two words can be connected in a word ladder chain if they differin exactly one letter.As an example, the following word ladder connects green and brown.

    green greet great groat groan grown brown

    You can also try out your program on this list of6 letter words.

12. Faster word ladders.To speed things up (if the word list is very large),don't write a nested loop to try all pairs ofwords to see if they are adjacent. To handle 5 letter words,first sort the word list. Words that only differ in their last letterwill appear consecutively in the sorted list. Sort 4 more times,but cyclically shift the letters one position to the right sothat words that differ in the ith letter will appear consecutivelyin one of the sorted lists.

    Try out this approach using a largerword list with words of different sizes. Two words of differentlengths are neighbors if the smaller word is the same as the biggerword, minus the last letter, e.g., brow and brown.

13. Suppose you delete all of the bridges in an undirected graph.Are the connected components of the resulting graph the biconnected components?Answer: no, two biconnected components can be connected through anarticulation point.

    Bridges and articulation points.

    A bridge (or cut edge) is an edge whose removal disconnectsthe graph.An articulation point (or cut vertex) is a vertex whoseremoval (and removal of all incident edges)disconnects the remaining graph.Bridges and articulations points are important because theyrepresent a single point of failure in a network.Brute force: delete edge (or vertex) and check connectivity.Takes O(E(V + E)) and O(V(V + E)) time, respectively.Can improve both to O(E + V) using clever extension to DFS.
14. Biconnected components.An undirected graph is biconnected if for every pairof vertices v and w, there are two vertex-disjoint paths betweenv and w. (Or equivalently a simple cycle through any two vertices.)We define a cocyclicity equivalence relation on the edges:two edges e1 and e2 are are in same biconnected component if e1 = e2 or thereexists a cycle containing both e1 and e2.Two biconnected components share at most one vertex in common.A vertex is an articulation point if and only if it is common to more than one biconnectedcomponent.Program Biconnected.javaidentifies the bridges and articulation points.
15. Biconnected components.Modify Biconnected to print out the edges that constituteeach biconnected component.Hint: each bridge is its own biconnected component;to compute the other biconnected components, mark each articulation pointas visited, and then run DFS, keeping track of the edges discoveredfrom each DFS start point.
16. Perform numerical experiments on the number of connected components for random undirected graphs.Phase change around 1/2 V ln V.(See Property 18.13 in Algs Java.)
17. Rogue. (Andrew Appel.)A monster and a player are each located at a distinct vertexin an undirected graph. In the role playing game Rogue,the player and the monster alternate turns. In each turnthe player can move to an adjacent vertex or stays put.Determine all vertices that the player can reach before the monster. Assume the player gets the first move.
18. Rogue. (Andrew Appel.)A monster and a player are each located at a distinct vertexin an undirected graph. The goal of the monster is toland on the same vertex as the player. Devise an optimal strategyfor the monster.
19. Articulation point.Let G be a connected, undirected graph. Consider a DFS tree for G.Prove that vertex v is an articulation point of G if and only if either (i) v is the root of the DFS tree and has more than one childor (ii) v is not the root of the DFS tree and for some child w of v there is no back edge between any descendant of w (including w)and a proper ancestor of v.In other words, v is an articulation point if and only if (i) v is the rootand has more than one child or (ii) v has a child w such thatlow[w] >= pre[v].
20. Sierpinski gasket.Nice example of an Eulerian graph.
21. Preferential attachment graphs.Create a random graph on V vertices and E edges as follows: start with V vertices v1, .., vn inany order. Pick an element of sequence uniformlyat random and add to end of sequence. Repeat 2Etimes (using growing list of vertices). Pair up the last 2E vertices to form the graph.

    Roughly speaking, it's equivalent to addingeach edge one-by-one with probability proportional to theproduct of the degrees of the two endpoints.Reference.

22. Wiener index.The Wiener index of a vertex is the sum of the shortest path distances between v andall other vertices.The Wiener index of a graph G is the sum of the shortest path distances overall pairs of vertices.Used by mathematical chemists (vertices = atoms, edges = bonds).
23. Random walk.Easy algorithm for getting out of a maze (or st connectivityin a graph): at each step, takea step in a random direction.With complete graph, takes V log V time (coupon collector);for line graph or cycle, takes V^2 time (gambler's ruin).In general the cover time is at most 2E(V-1), a classic result ofAleliunas, Karp, Lipton, Lovasz,and Rackoff.
24. Deletion order.Given a connected graph, determine an order to delete the vertices such thateach deletion leaves the (remaining) graph connected. Your algorithm should taketime proportional to V + E in the worst case.
25. Center of a tree.Given a graph that is a tree (connected and acyclic), find a vertexsuch that its maximum distance from any other vertex is minimized.

    Hint: find the diameter of the tree (the longest path betweentwo vertices) and return a vertex in the middle.

26. Diameter of a tree.Given a graph that is a tree (connected and acyclic),find the longest path, i.e.,a pair of vertices v and w that are as far apart as possible.Your algorithm should run in linear time.

    Hint.Pick any vertex v. Compute the shortest path from v to every other vertex. Let wbe the vertex with the largest shortest path distance.Compute the shortest path from w to every other vertex.Let x be the vertex with the largest shortest path distance.The path from w to x gives the diameter.

27. Bridges with union-find.Let T be a spanning tree of G. Each non-tree edge e in G forms a fundamental cycleconsisting of the edge e plus the unique path in the tree joining its endpoings.Show that an edge is a bridge if and only if it is not on some fundamental cycle.Thus, all bridges ar edges of the spanning tree. Design an algorithm to find allof the bridge and bridge components using E + V time plus E + V union-find operations.
28. Matlab connected components. bwlabel() or bwlabeln() in Matlab label the connected components in a 2D or kDbinary image. bwconncomp() is newer version.

Last modified on April 02, 2013.

http://algs4.cs.princeton.edu/41undirected/