hdu 4475 Downward paths
来源:互联网 发布:js 数组循环添加对象 编辑:程序博客网 时间:2024/06/08 07:02
Downward paths
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)Total Submission(s): 350 Accepted Submission(s): 106
Problem Description
================
Hi! I am an ACMer from CSU. This contest made by me is to celebrate my girlfriend’s birthday although the problems in this contest do not relate to her in fact. :) Any way, happy birthday to you, honey!
Thanks to LCY, I have this chance to share my ideas and works with you. Good luck and have fun!
================
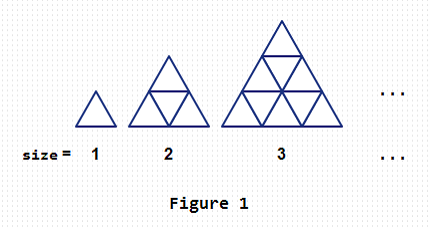
We have a graph with size = N like that in Figure 1. Then we are going to find a downward path from the top node to one bottom node.
First, we select the top node as the beginning. Then at any node, we can go horizontally or downward along the blue edge and reach the next node. The finding will be end when we reach one of the bottom nodes. After that we can get a downward path from the top node to one bottom node. Note that we can not pass a blue edge that we have passed ago during each finding.
Your task is to calculate there exists how many downward paths.
Hi! I am an ACMer from CSU. This contest made by me is to celebrate my girlfriend’s birthday although the problems in this contest do not relate to her in fact. :) Any way, happy birthday to you, honey!
Thanks to LCY, I have this chance to share my ideas and works with you. Good luck and have fun!
================
We have a graph with size = N like that in Figure 1. Then we are going to find a downward path from the top node to one bottom node.
First, we select the top node as the beginning. Then at any node, we can go horizontally or downward along the blue edge and reach the next node. The finding will be end when we reach one of the bottom nodes. After that we can get a downward path from the top node to one bottom node. Note that we can not pass a blue edge that we have passed ago during each finding.
Your task is to calculate there exists how many downward paths.

Input
There is an integer T (1 <= T <= 1000) in the first line, which indicates there are T test cases in total.
For each test case, there is only one integer N (1 <= N <= 10^18) indicates the size of the graph.
For each test case, there is only one integer N (1 <= N <= 10^18) indicates the size of the graph.
Output
For each test case, you should output the correct answer of the above task in one line.
Because the answer may be very large, you should just output the remainder of it divided by 1000003.
Because the answer may be very large, you should just output the remainder of it divided by 1000003.
Sample Input
212
Sample Output
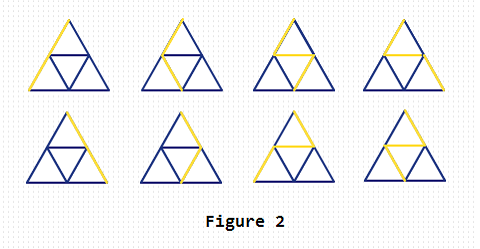
28HintFor Sample 2, the yellow paths in Figure 2 show the 8 downward paths.
设size=i,答案是ai;
a1=2=1+1;
a2=8=2+2*2+2;
a3=48=8+8*2+8*2+8;
a4=384 =48+48*2+48*2+48*2+48;
......
很明显规律:an=an-1+2*(n-1)an-1+an-1=2*n*an-1;
即:an=2^n*n!
注意:1.an=2^n*n!,,,所以当n>1000003时,n!中有1000003这个因数,故ans=0,
AC代码:
#include <iostream>#include <cstring>#define mod 1000003using namespace std;long long a[mod+5];int main(){ int t; long long n; a[0]=0; a[1]=2; for(int i=2;i<mod;i++) a[i]=a[i-1]*2*i%mod; cin>>t; while(t--) { cin>>n; if(n>=mod) cout<<"0"<<endl; else cout<<a[n]<<endl; }return 0;}
- HDU 4475 Downward paths
- hdu 4475 Downward paths
- HDU 4475 Downward paths (找规律)
- HDU-4475 Downward paths(找规律)
- HDU-1625-Numbering Paths
- HDU 6181 Two Paths
- HDU 6181 Two Paths
- hdu 6181 Two Paths
- Two Paths HDU
- HDU 1293 The Number of Paths
- HDU 4912 Paths on the tree
- hdu 4912 Paths on the tree
- hdu 4912Paths on the tree (LCA)
- HDU-4912-Paths on the tree
- HDU 3191 How Many Paths Are There
- The Number of Paths - HDU 1293 DP
- HDU-3191-How Many Paths Are There
- hdu 1625 Numbering Paths floyd变形
- C# 读取PE
- ASP.NET 总结
- UVA 10131 Is Bigger Smarter? DP
- JS学习记录(二)
- 三层结构剖析
- hdu 4475 Downward paths
- flascc——Flash调用C++库的方法和工具
- C#Task 学习 二
- BZOJ1500 维护数列 treap实现
- 任意范围,任意类型的随机数生成器
- 详解大端模式和小端模式
- Qt一些鲜为人知的小功能
- WIN32 listview用法
- 鼠标右键失灵 解决鼠标右键失灵方法