【Machine Learning】SVM学习笔记

理解Support Vector Machine

小弟最近在研究SVM方面的理论，写这篇文章来总结一下我的理解。

首先吐个槽，外国人有个毛病，稍微整个什么新的东西出来就要起个矫情的名字，让人觉得很高深。也许是我修行不够，不能理解其深奥的含义，但是好歹也得起个好理解的名字吧，直译过来”支持向量机“，这到底什么玩意儿？其实所谓”支持向量“，就是由影响决策平面（classifier）的点和原点形成而已，稍后再叙。

1、初窥SVM.

SVM可以理解为一个比较robust的分类器，简单的SVM可以把线性可分的点集分成两个部分。

2、简单的SVM

为简单起见，以二维平面中线性可分点集{xi,yi}, i=1,...,n， y∈{-1,+1}为例，要寻找出一条直线，使其到两类点的最短距离的和最大。这个最短距离的和可以称之为margin。SVM就是要找这个直线，并且最大化margin。

上面一段提到，SVM是一个比较robust的分类器。原因就在于SVM使得margin最大化，保证在距离某一类点集一段距离内，都可以被判断为属于该点集，这样可以降低小扰动带来的影响，提高正确率。

在多维情况下，该直线变为超平面（hyperplane）。

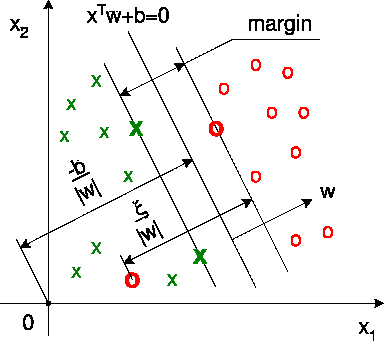
2.1、超平面（/直线）条件的确定

超平面的确定于直线相类似，w·x + b=0,其中 |b|/||w||为超平面到原点的垂直距离。只不过，这里斜率部分和自变量部分为向量表示。其算法主要是在于确定斜率向量和b中元素，以求margin最大（算法的核心就是线性规划，如果转化得当，可以用现有的linear programming solver）。

考虑用于训练的二维二元可分点集，可以得到如下约束条件：

w·xi+ b ≥ +1 （yi = +1） 【1】

w·xi+ b ≤ -1 （yi = -1） 【2】

上述两个约束条件可以总结为：

yi(w·xi+ b)-1 ≥ 0  （对于任意 i ）【3】

考虑【1】中刚好在线上的点，这些点就是+1集的临界点，可以确定未知量的范围。那么在等号成立条件下【1】可以确定出来的超平面H1，到远点的距离就是

|b-1|/||w||， 同理【2】中等号成立时，确定H2，到原点距离为|b+1|/||w||，因为w相同，可以理解为H1和H2平行，那么margin就可以很方便的用上面的结果表示，即为：2/||w||。那么，最大化margin就等同于最小化||w||^2.

2.2、超平面参数确定的算法——拉格朗日乘子

根据上面的论述，在某线性条件下最小化某一个量，这是一个优化问题，而且目标函数是一个非线性的。仅作基于拉格朗日乘子法（Lagrange Multipliers）的理论推导(点击英文看英文版的那个吧，说的和画的都很清楚，不过这个是多元微积分必讲的内容，应该还有点儿印象。小弟也在琢磨优化的问题，等有一定理解再总结一下)。

言归正传，虽然【3】看似很简单，但其实我们有n个训练样本，因此就会有n个像【3】那样的约束，所以我们需要有n个乘子ai，i = 1,...,n。这里需要提一下，对于像ki≥0这样的约束条件，与其对应的乘子ai≥0。我们可以得到拉格朗日表达式为：

L=||w||^2/2-Σai·yi(w·xi+ b) +Σai 【5】

其中Σ下限为1，上限为n。以w和b为自变量，对L最小化，因此需要L对ai的倒数全为0. 我们感兴趣的是w和b，L对ai的导数并没有太大意义，还好有一个wolfe duality，可以将问题稍作转化，成为等价的另一个表达式Ld。两表达式源自同一优化对象方程，但是用的条件不同。最大化L，条件是L对w和b的导数为0，而且ai≥0。这与ai导数为0，L最小化所得到的优化结果一致。

w=Σai·yi·xi 【6】

Σai·yi=0   【7】

将【6】【7】带入【5】中，因而得到

Ld=Σai -Σai·aj·yi·yj·xj·xi 【8】

综上，我们需要以ai为自变量最大化【8】，而且要满足条件【7】。解出拉格朗日乘子。

结果w可以根据式【6】求出，选择ai!=0的点，带入【1】或【2】中，令等式成立，算出b。其中ai!=0的点就是"support vector".

2.3、【8】式如何解？！——Kernal Function

我们刚刚接触到求解SVM中第一个技巧——dual problem，转化了拉格朗日乘子法的形式。 下面的问题就是为啥要转化成这个形式。首先我们要回顾一下，SVM的hypothesis是什么？ 其实跟neuro-network类似，是分割平面，只不过SVM的分割平面被称为超平面，顾名思义，就是这个分割平面被定义在了更高的纬度上。具体来讲，如果再n维空间里的点集不能在该空间内分割，那么把这些点通过某种函数f 扩展到更高纬度（n+1维），那么就会比较容易得找到新的（n+1维）分割平面。那现在的问题就是找到f，把上【8】中所述的xi进行某种变换f(xi),使其扩展到更高纬度。有很多人汇问道，嗯，f的具体形式是啥？这就是SVM另外一个技巧！观察【8】，实际上我们并不需要显式的知道变换的形式，因为在【8】中，起到影响作用的是内积xj·xi，所以，我们只要知道他们内积的形式就可以了。这个问题就简化成了怎么定义这个高维空间的内积。这个技巧牵扯到的东西就是Kernal Function，简而言之，Kernal Function就是定义了两个向量扩展到高维后的内积形式，K(x,y) 。常用的kernal已经被定义出来，包括高斯核...通过Kernal Function, 就可以方便的计算出内积，至此，问题就被转化成了普通的优化问题。

3、SVM的使用

为方便使用，研究人员公布了SVM的算法库，包括libsvm（C），opencv中的svm模块（C/C++），matlab里面的toolbox，以供我们这些不是专门研究Machine Learning的人。我本人因为最近在做CV的研究，经常使用到opencv，也在使用它的svm模块，虽然没有专用的库灵活，但是也够用了。使用方法很傻瓜，在这里就不赘述了。

另外，CSDN是不是可以支持一下latex啊，这么打公式好疼啊。