hdu 3516 Tree Construction

Tree Construction

Time Limit: 4000/2000 MS (Java/Others)    Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 684    Accepted Submission(s): 364

Problem Description

Consider a two-dimensional space with a set of points (xi, yi) that satisfy xi < xj and yi > yj for all i < j. We want to have them all connected by a directed tree whose edges go toward either right (x positive) or upward (y positive). The figure below shows an example tree.


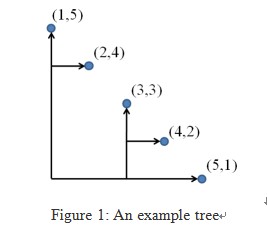
Write a program that finds a tree connecting all given points with the shortest total length of edges.

 

Input

The input begins with a line that contains an integer n (1 <= n <= 1000), the number of points. Then n lines follow. The i-th line contains two integers xi and yi (0 <= xi, yi <= 10000), which give the coordinates of the i-th point.

 

Output

Print the total length of edges in a line.

 

Sample Input

51 52 43 34 25 1110000 0

 

Sample Output

120

 

Source

2010 ACM-ICPC Multi-University Training Contest（8）——Host by ECNU

 

Recommend

zhouzeyong

 【题目意思】给你很多个点，这些点满足a set of points (xi, yi) that satisfy xi < xj and yi > yj for all i < j.让你用一棵树把所有点连在一齐，树只能往上跟右生长，求树的总长度最小
【解题思路】类似石子合并，加上四边形优化就行了
定义状态 dp[i,j]表示点i到点j合并在一起的最小花费（树枝的长度），
状态转移方程：dp[i,j]= min(dp[i,k]+dp[k+1,j]+cost(i,j) ) i<k<j
cost(i,j)=py[k]-py[j]+px[k+1]-px[i];
当j固定时，cost(i,j)单调递减函数
我们猜测cost(i,j)满足四边形不等式
证明： 
F(i)=cost(i,j+1)-cost(i,j)=py[j]-py[j+1]是一个与i无关的多项式，
所以j固定时，F(i)满足四边形不等式，得证。
s[i,j]=k;s[i-1,j] <= s[i,j] <= s[i,j+1];
由于决策s具有单调性,因此状态转移方程可修改为:
dp[i,j]= min(dp[i,k]+dp[k+1,j]+cost(i,j) ) s[i-1,j] <=k<= s[i,j+1];
开始轻松的写出了动态方程：
dp[i][j]=MIN(dp[i][k]+dp[k+1][j]+x[k+1]-x[i]+y[k]-y[j]  i<=k<=j
于是写了一个朴素枚举的程序。果断超时了。百思不得其解。搜了下题解才知道要
用四边形不等式优化。即缩小枚举范围时间发杂度降到o(n^2)。四边形不等式一片
空白。这是我第一个四边形不等式优化dp。看了各种资料后终于明白大部分思想了
就是四边形条件不好证明。不过简单运用会点了。dp依然很菜。继续加油！

#include <iostream>#include<stdio.h>#include<string.h>#define MAX(a,b) ((a)>(b)?(a):(b))#define MIN(a,b) ((a)<(b)?(a):(b))#define positive(a) ((a)>0?(a):-(a))using namespace std;int x[1010],y[1010];//记录x,y坐标int n,ans,dp[1010][1010],s[1010][1010];void solve(){    int i,j,k,len,l,r,temp;    memset(dp,0x3f,sizeof dp);    for(i=1;i<=n;i++)    {        dp[i][i]=0;//把自己连接起来肯定需要0        s[i][i]=i;//初始为k的枚举范围为i到i。    }    for(len=2;len<=n;len++)//枚举区间长度。由动态方程    {                      //dp[i][j]=MIN(dp[i][k]+dp[k+1][j]+x[k+1]-x[i]+y[k]-y[j]                           //可知dp[i][k],dp[k+1][j]均是比dp[i][j]小的区间为了计算dp[i][j]必须算出比                           //其小的区间dp。所以从小到大枚举区间长度        for(i=n-len+1;i>0;i--)//i必须从大到小枚举。因为计算dp[i][j]时要用到dp[i][k],dp[k+1][j]                             //k+1>i所以为了保证k+1已经算出必须倒着枚举        {            j=i+len-1;            l=s[i][j-1];//由四边形不等式s[i][j-1]<=k<=s[i+1][j]            r=MIN(j-1,s[i+1][j]);//计算s[i][j]需要s[i][j-1]和s[i+1][j]                                 //s[i+1][j]前面已算出.s[i][j-1]范围比s[i][j]小也已算出            for(k=l;k<=r;k++)//枚举l,r，之间的k即可            {                temp=dp[i][k]+dp[k+1][j]+x[k+1]-x[i]+y[k]-y[j];                if(temp<dp[i][j])                {                    dp[i][j]=temp;                    s[i][j]=k;//得出i和j之间枚举k的范围为i到k                }            }        }    }    ans=dp[1][n];}int main(){    int i;    while(~scanf("%d",&n))    {        for(i=1;i<=n;i++)            scanf("%d%d",x+i,y+i);        solve();        printf("%d\n",ans);    }    return 0;}