Algebra Applied Mathematics Calculus and Analysis Discrete Mathematics Foundations of Mathematic
来源:互联网 发布:云计算介绍 编辑:程序博客网 时间:2024/04/27 21:48

Last updated: Mon Jul 29 2013
Circle
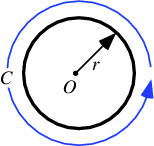
A circle is the set of points in a plane that are equidistant from a given point ![]() . The distance
. The distance ![]() from the center is called the radius, and the point
from the center is called the radius, and the point ![]() is called the center. Twice the radius is known as the diameter
is called the center. Twice the radius is known as the diameter ![]() . The angle a circle subtends from its center is a full angle, equal to
. The angle a circle subtends from its center is a full angle, equal to ![]() or
or ![]() radians.
radians.
A circle has the maximum possible area for a given perimeter, and the minimum possible perimeter for a given area.
The perimeter ![]() of a circle is called the circumference, and is given by
of a circle is called the circumference, and is given by
This can be computed using calculus using the formula for arc length in polar coordinates,
but since ![]() , this becomes simply
, this becomes simply
The circumference-to-diameter ratio ![]() for a circle is constant as the size of the circle is changed (as it must be since scaling a plane figure by a factor
for a circle is constant as the size of the circle is changed (as it must be since scaling a plane figure by a factor ![]() increases its perimeter by
increases its perimeter by ![]() ), and
), and ![]() also scales by
also scales by ![]() . This ratio is denoted
. This ratio is denoted ![]() (pi), and has been proved transcendental.
(pi), and has been proved transcendental.
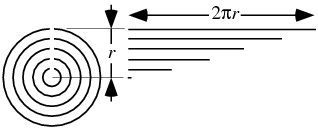
Knowing ![]() , the area of the circle can be computed either geometrically or using calculus. As the number of concentric strips increases to infinity as illustrated above, they form a triangle, so
, the area of the circle can be computed either geometrically or using calculus. As the number of concentric strips increases to infinity as illustrated above, they form a triangle, so
This derivation was first recorded by Archimedes in Measurement of a Circle (ca. 225 BC).
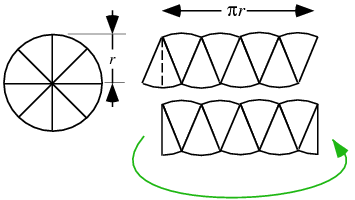
If the circle is instead cut into wedges, as the number of wedges increases to infinity, a rectangle results, so
From calculus, the area follows immediately from the formula
again using polar coordinates.
A circle can also be viewed as the limiting case of a regular polygon with inradius ![]() and circumradius
and circumradius ![]() as the number of sides
as the number of sides ![]() approaches infinity (a figure technically known as an apeirogon). This then gives the circumference as
approaches infinity (a figure technically known as an apeirogon). This then gives the circumference as
and the area as
which are equivalently since the radii ![]() and
and ![]() converge to the same radius as
converge to the same radius as ![]() .
.
Unfortunately, geometers and topologists adopt incompatible conventions for the meaning of "![]() -sphere," with geometers referring to the number of coordinates in the underlying space and topologists referring to the dimension of the surface itself (Coxeter 1973, p. 125). As a result, geometers call the circumference of the usual circle the 2-sphere, while topologists refer to it as the 1-sphere and denote it
-sphere," with geometers referring to the number of coordinates in the underlying space and topologists referring to the dimension of the surface itself (Coxeter 1973, p. 125). As a result, geometers call the circumference of the usual circle the 2-sphere, while topologists refer to it as the 1-sphere and denote it ![]() .
.
The circle is a conic section obtained by the intersection of a cone with a plane perpendicular to the cone's symmetry axis. It is also a Lissajous curve. A circle is the degenerate case of an ellipse with equal semimajor and semiminor axes (i.e., with eccentricity 0). The interior of a circle is called a disk. The generalization of a circle to three dimensions is called a sphere, and to ![]() dimensions for
dimensions for ![]() a hypersphere.
a hypersphere.
The region of intersection of two circles is called a lens. The region of intersection of three symmetrically placed circles (as in a Venn diagram), in the special case of the center of each being located at the intersection of the other two, is called a Reuleaux triangle.
In Cartesian coordinates, the equation of a circle of radius ![]() centered on
centered on ![]() is
is
In pedal coordinates with the pedal point at the center, the equation is
The circle having ![]() as a diameter is given by
as a diameter is given by
The parametric equations for a circle of radius ![]() can be given by
can be given by
The circle can also be parameterized by the rational functions
but an elliptic curve cannot.
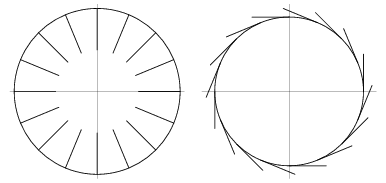
The plots above show a sequence of normal and tangent vectors for the circle.
The arc length ![]() , curvature
, curvature ![]() , and tangential angle
, and tangential angle ![]() of the circle with radius
of the circle with radius ![]() represented parametrically by (◇) and (◇) are
represented parametrically by (◇) and (◇) are
The Cesàro equation is
In polar coordinates, the equation of the circle has a particularly simple form.
is a circle of radius ![]() centered at origin,
centered at origin,
is circle of radius ![]() centered at
centered at ![]() , and
, and
is a circle of radius ![]() centered on
centered on ![]() .
.
The equation of a circle passing through the three points ![]() for
for ![]() , 2, 3 (the circumcircle of the triangle determined by the points) is
, 2, 3 (the circumcircle of the triangle determined by the points) is
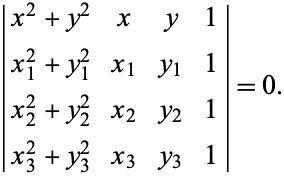
The center and radius of this circle can be identified by assigning coefficients of a quadratic curve
where ![]() and
and ![]() (since there is no
(since there is no ![]() cross term). Completing the square gives
cross term). Completing the square gives
The center can then be identified as
and the radius as
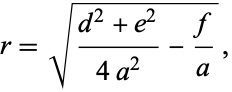
where

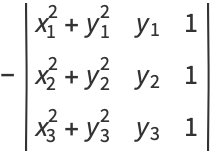
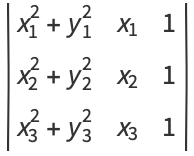
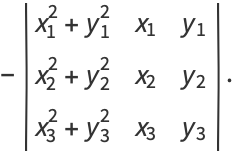
Four or more points which lie on a circle are said to be concyclic. Three points are trivially concyclic since three noncollinear points determine a circle.
In trilinear coordinates, every circle has an equation of the form
with ![]() (Kimberling 1998, p. 219).
(Kimberling 1998, p. 219).
The center ![]() of a circle given by equation (35) is given by
of a circle given by equation (35) is given by
(Kimberling 1998, p. 222).
In exact trilinear coordinates ![]() , the equation of the circle passing through three noncollinear points with exact trilinear coordinates
, the equation of the circle passing through three noncollinear points with exact trilinear coordinates ![]() ,
, ![]() , and
, and ![]() is
is
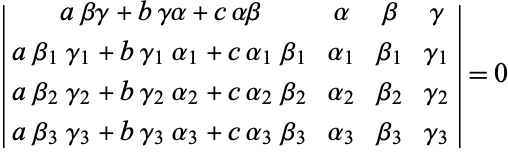
(Kimberling 1998, p. 222).
An equation for the trilinear circle of radius ![]() with center
with center ![]() is given by Kimberling (1998, p. 223).
is given by Kimberling (1998, p. 223).
Wolfram Web Resources
Mathematica »The #1 tool for creating Demonstrations and anything technical.
Wolfram|Alpha »Explore anything with the first computational knowledge engine.
Wolfram Demonstrations Project »Explore thousands of free applications across science, mathematics, engineering, technology, business, art, finance, social sciences, and more.
Computable Document Format »The format that makes Demonstrations (and any information) easy to share and interact with.
STEM initiative »Programs & resources for educators, schools & students.
Computerbasedmath.org »Join the initiative for modernizing math education.
- Algebra Applied Mathematics Calculus and Analysis Discrete Mathematics Foundations of Mathematic
- outline of discrete mathematics and its applications(1.1-1.3)
- outline of discrete mathematics and its applications(1.4-1.7)
- outline of discrete mathematics and its applications(2.1-2.3)
- outline of discrete mathematics and its applications(9.1-9.6)
- A Java Library of Graph Algorithms and Optimization (Discrete Mathematics and Its Applications)
- Topics on Discrete Mathematics
- matrix analysis and applied linear algebra
- notes for "Discrete Mathematics and its Application" : Chapter one
- Mathematics
- Mathematics
- Mathematics
- Applied Mathematics for Database Professionals
- 【Discrete Mathematics】Template Method Pattern
- The beauty of mathematics
- Mathematics of Motion Control
- 1869: Mathematics and Geometry
- 经典书Discrete.Mathematics上的大神
- 自己存档
- MFC里 CString 转char*
- 关于 epoll 的文章
- 中断、异常和系统调用
- Mono For Android 重要的类文件
- Algebra Applied Mathematics Calculus and Analysis Discrete Mathematics Foundations of Mathematic
- Android应用开发学习笔记之startActivityForResult
- C# Double保留小数点后面位数
- /usr/bin/ld: cannot find -lrt-wmp
- JS 判断上传文件是否为EXCEL 文件
- Makefile automatic variables
- android.graphics.Typeface实践 字体风格
- 数据库范式
- hdu 1237
 circle
circle
 Area between a Line and the Graph of a Function
Area between a Line and the Graph of a Function How Area Changes with Diameter
How Area Changes with Diameter Problems on Circles XIII: Common Area of Two Circles
Problems on Circles XIII: Common Area of Two Circles Problems on Circles X: Tangent Circles Generate Ellipses
Problems on Circles X: Tangent Circles Generate Ellipses


