协方差与自相关
来源:互联网 发布:sql join 编辑:程序博客网 时间:2024/05/11 13:03
协方差矩阵是一个矩阵,其每个元素是各个向量元素之间的协方差。这是从标量随机变量到高维度随机向量的自然推广。
假设 是以
是以 个标量随机变量组成的列向量,
个标量随机变量组成的列向量,
并且 是其第i个元素的期望值,即,
是其第i个元素的期望值,即, 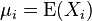 。协方差矩阵被定义的第i,j项是如下:
。协方差矩阵被定义的第i,j项是如下:
即:
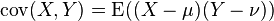 ,
, ,
,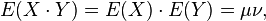
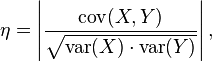
![\, \gamma(i,j) = E[(X_i - \mu_i)(X_j - \mu_j)].\,](http://upload.wikimedia.org/math/5/d/2/5d2a66040067bddd3645095e9c8870d7.png)
![\, \gamma(k) = E[(X_i - \mu)(X_{i-k} - \mu)].\,](http://upload.wikimedia.org/math/5/0/a/50a1fab41322d9357c5fc05fdf28dee1.png)

![R(k) = \frac{E[(X_i - \mu_i)(X_{i+k} - \mu_{i+k})]}{\sigma^2}](http://upload.wikimedia.org/math/0/3/9/0391e96b20b9d3d0716119516178be93.png)
 ......... 期望值。
......... 期望值。 ........ 在t(i)时的随机变量值。
........ 在t(i)时的随机变量值。 ........ 在t(i)时的预期值。
........ 在t(i)时的预期值。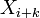 .... 在t(i+k)时的随机变量值。
.... 在t(i+k)时的随机变量值。 .... 在t(i+k)时的预期值。
.... 在t(i+k)时的预期值。 ......... 为方差。
......... 为方差。
![=\begin{bmatrix} \mathrm{E}[(X_1 - \mu_1)(X_1 - \mu_1)] & \mathrm{E}[(X_1 - \mu_1)(X_2 - \mu_2)] & \cdots & \mathrm{E}[(X_1 - \mu_1)(X_n - \mu_n)] \\ \\ \mathrm{E}[(X_2 - \mu_2)(X_1 - \mu_1)] & \mathrm{E}[(X_2 - \mu_2)(X_2 - \mu_2)] & \cdots & \mathrm{E}[(X_2 - \mu_2)(X_n - \mu_n)] \\ \\ \vdots & \vdots & \ddots & \vdots \\ \\ \mathrm{E}[(X_n - \mu_n)(X_1 - \mu_1)] & \mathrm{E}[(X_n - \mu_n)(X_2 - \mu_2)] & \cdots & \mathrm{E}[(X_n - \mu_n)(X_n - \mu_n)]\end{bmatrix}](http://upload.wikimedia.org/math/a/1/2/a12a573ecd1d853abd8c01fab9fccfbe.png)
期望值分别为
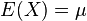 与
与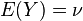 的两个实数随机变量X 与Y 之间的协方差定义为:
的两个实数随机变量X 与Y 之间的协方差定义为:其中E是期望值。它也可以表示为:
如果X 与Y 是统计独立的,那么二者之间的协方差就是0,这是因为
但是反过来并不成立,即如果X 与Y 的协方差为0,二者并不一定是统计独立的。
取决于协方差的相关性η
更准确地说是线性相关性,是一个衡量线性独立的无量纲数,其取值在[0,+1]之间。相关性η = 1时称为“完全线性相关”,此时将Yi对Xi作Y-X 散点图,将得到一组精确排列在直线上的点;相关性数值介于0到1之间时,其越接近1表明线性相关性越好,作散点图得到的点的排布越接近一条直线。
在统计学中,特定时间序列或者连续信号 Xt 的自协方差是信号与其经过时间平移的信号之间的协方差。如果序列的每个状态都有一个平均数 E[Xt] = μt,那么自协方差为
其中 E 是期望值运算符。如果 Xt 是二阶平稳过程,那么有更加常见的定义:
其中 k 是信号移动的量值,通常称为延时。如果用方差 σ2 进行归一化处理,那么自协方差就变成了自相关系数R(k),即
需要注意的是,在有些学科中自协方差术语等同于自相关。
将一个有序的随机变量系列与其自身相比较,这就是自相关函数在统计学中的定义。每个不存在相位差的系列,都与其自身相似,即在此情况下,自相关函数值最大。如果系列中的组成部分相互之间存在相关性(不再是随机的),则由以下相关值方程所计算的值不再为零,这样的组成部分为自相关。
所得的自相关值R的取值范围为[-1,1],1为最大正相关值,-1则为最大负相关值,0为不相关。
- 协方差与自相关
- 自协方差函数,自相关函数,协方差矩阵
- 自相关函数和自协方差函数
- 在主成分分析中的协方差矩阵与自相关矩阵的差别
- 协方差与协方差矩阵
- 协方差与协方差矩阵
- 协方差与协方差矩阵
- 协方差与协方差矩阵
- 详解协方差与协方差矩阵
- 详解协方差与协方差矩阵
- 详解协方差与协方差矩阵
- 详解协方差与协方差矩阵
- 详解协方差与协方差矩阵
- 详解协方差与协方差矩阵
- 详解协方差与协方差矩阵
- 详解协方差与协方差矩阵 .
- 详解协方差与协方差矩阵
- 浅谈协方差与协方差矩阵
- 如何在ubuntu13.04启动ssh
- 各种编程语言和方式对比
- 数位dp+LIS+状态压缩-hdu-4352-XHXJ's LIS
- 系统设计之粒度控制
- Java 基础加强 - 反射Reflect
- 协方差与自相关
- 如何在GWT实现点击Button(或其他Widget)打开文件选择对话框
- HDOJ,杭电1877,又一版A+B。。又是进制转化的题目。。
- HTTP协议详解
- [Friends]S03E01
- 数学专项counting:LA 3720
- JavaScript加强之this
- 系统设计之架构设计
- NSMutableArray用法
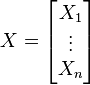

![\Sigma=\mathrm{E}\left[ \left( \textbf{X} - \mathrm{E}[\textbf{X}] \right) \left( \textbf{X} - \mathrm{E}[\textbf{X}] \right)^\top\right]](http://upload.wikimedia.org/math/1/8/1/1811f942680a72974597be42c28d31d2.png)


