多项式长除法

来源：互联网发布：newa美容仪知乎编辑：程序博客网时间：2024/04/30 04:48

多项式长除法是代数中的一种算法，用一个同次或低次的多项式去除另一个多项式。是常见算数技巧长除法的一个推广版本。它可以很容易地手算，因为它将一个相对复杂的除法问题分解成更小的一些问题。

例[编辑]计算

$\frac{x^3 - 12x^2 - 42}{x-3}.$

把被除式、除式按某个字母作降幂排列，并把所缺的项用零补齐，写成以下这种形式：

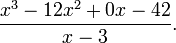
$\frac{x^3 - 12x^2 + 0x - 42}{x-3}.$

然后商和余数可以这样计算：

将分子的第一项除以分母的最高次项（即次数最高的项，此处为x）。结果写在横线之上(x³ ÷ x = x²).

$\begin{matrix}x^2\\\qquad\qquad\quad x-3\overline{) x^3 - 12x^2 + 0x - 42}\end{matrix}$
将分母乘以刚得到结果（最终商的第一项），乘积写在分子前两项之下（同类项对齐） (x² · (x − 3) = x³ − 3x²).
$\begin{matrix}x^2\\\qquad\qquad\quad x-3\overline{) x^3 - 12x^2 + 0x - 42}\\\qquad\;\; x^3 - 3x^2\end{matrix}$
从分子的相应项中减去刚得到的乘积（消去相等项，把不相等的项结合起来），结果写在下面。((x³ − 12x²) − (x³ − 3x²) = −12x² + 3x² = −9x²)然后，将分子的下一项“拿下来”。
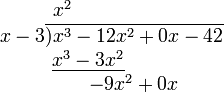
$\begin{matrix}x^2\\\qquad\qquad\quad x-3\overline{) x^3 - 12x^2 + 0x - 42}\\\qquad\;\; \underline{x^3 - 3x^2}\\\qquad\qquad\qquad\quad\; -9x^2 + 0x\end{matrix}$
把减得的差当作新的被除式，重复前三步（直到余式为零或余式的次数低于除式的次数时为止．被除式=除式×商式+余式）
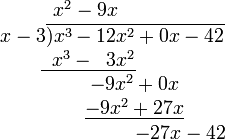
$\begin{matrix}\; x^2 - 9x\\\qquad\quad x-3\overline{) x^3 - 12x^2 + 0x - 42}\\\;\; \underline{\;\;x^3 - \;\;3x^2}\\\qquad\qquad\quad\; -9x^2 + 0x\\\qquad\qquad\quad\; \underline{-9x^2 + 27x}\\\qquad\qquad\qquad\qquad\qquad -27x - 42\end{matrix}$
重复第四步。这次没什么可以“拿下来”了。
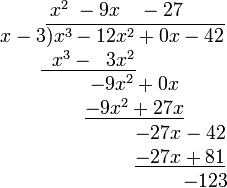
$\begin{matrix}\qquad\quad\;\, x^2 \; - 9x \quad - 27\\\qquad\quad x-3\overline{) x^3 - 12x^2 + 0x - 42}\\\;\; \underline{\;\;x^3 - \;\;3x^2}\\\qquad\qquad\quad\; -9x^2 + 0x\\\qquad\qquad\quad\; \underline{-9x^2 + 27x}\\\qquad\qquad\qquad\qquad\qquad -27x - 42\\\qquad\qquad\qquad\qquad\qquad \underline{-27x + 81}\\\qquad\qquad\qquad\qquad\qquad\qquad\;\; -123\end{matrix}$
横线之上的多项式即为商，而剩下的 (−123) 就是余数。

$\frac{x^3 - 12x^2 - 42}{x-3} = \underbrace{x^2 - 9x - 27}_{q(x)} \underbrace{-\frac{123}{x-3}}_{r(x)/g(x)}$

算数的长除法可以看做以上算法的一个特殊情形，即所有 x 被替换为10的情形。

除法变换[编辑]

使用多项式长除法可以将一个多项式写成除数-商的形式（经常很有用）。考虑多项式 P(x), D(x) （(D)的次数 < (P)的次数）。然后，对某个商多项式 Q(x) 和余数多项式 R(x) （(R)的系数 < (D)的系数），

$\frac{P(x)}{D(x)} = Q(x) + \frac{R(x)}{D(x)} \implies P(x) = D(x)Q(x) + R(x).$

这种变换叫做除法变换，是从算数等式 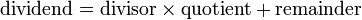${\mathrm{dividend} = \mathrm{divisor} \times \mathrm{quotient} + \mathrm{remainder} }$ .^[1] 得到的。

应用[编辑]

多项式的因式分解[编辑]

有时某个多项式的一或多个根已知，可能是使用 rational root theorem 得到的。如果一个 n 次多项式 P(x) 的一个根 r 已知，那么 P(x) 可以使用多项式长除法因式分解为 (x-r)Q(x) 的形式，其中 Q(x) 是一个 n-1 次的多项式。简单来说，Q(x) 就是长除法的商，而又知 r 是 P(x) 的一个根、余式必定为零。

相似地，如果不止一个根是已知的，比如已知 r 和 s 这两个，那么可以先从 P(x) 中除掉线性因子 x-r 得到 Q(x)，再从 Q(x) 中除掉 x-s，以此类推。或者可以一次性地除掉二次因子 x²-(r+s)x+rs。

使用这种方法，有时超过四次的多项式的所有根都可以求得，虽然这并不总是可能的。例如，如果 rational root theorem 可以用来求得一个五次方程的一个（比例）根，它就可以被除掉以得到一个四次商式；然后使用四次方程求根的显式公式求得剩余的根。

寻找多项式的切线[编辑]

多项式长除法可以用来在给定点上查找给定多项式的切线方程。^[2] 如果 R(x) 是 P(x)/(x-r)² 的余式——也即，除以 x²-2rx+r²——那么在 x=r 处 P(x) 的切线方程是 y=R(x)，不论 r 是否是 P(x) 的根。