Hinge loss

来源：互联网发布：绵阳互惠软件编辑：程序博客网时间：2024/04/28 16:55

Hinge loss

In machine learning, the hinge loss is a loss function used for training classifiers. The hinge loss is used for "maximum-margin" classification, most notably for support vector machines (SVMs).^[1] For an intended output t = ±1 and a classifier score y, the hinge loss of the prediction y is defined as

$\ell(y) = \max(0, 1-t \cdot y)$

Note that y should be the "raw" output of the SVM's decision function, not the predicted class label. E.g., in linear SVMs, $y = \mathbf{w} \cdot \mathbf{x} + b$ .

It can be seen that when $t$ and $y$ have the same sign (meaning $y$ predicts the right class) and $y \ge 1$ , $\ell(y) = 0$ (one-sided error), but when they have opposite sign, $\ell(y)$ increases linearly with $y$ .

Extensions[edit]

While SVMs are commonly extended to multiclass classification in a one-vs.-all or one-vs.-one fashion,^[2] there exists a "true" multiclass version of the hinge loss due to Crammer and Singer,^[3] defined for a linear classifier as^[4]

$\ell(y) = \max(0, 1 + \max_{y \ne t} \mathbf{w}_y \mathbf{x} - \mathbf{w}_t \mathbf{x})$

In structured prediction, the hinge loss can be further extended to structured output spaces. Structured SVMs use the following variant, where w denotes the SVM's parameters, φ the joint feature function, and Δ the Hamming loss:^[5]

$\begin{align}\ell(\mathbf{y}) & = \Delta(\mathbf{y}, \mathbf{t}) + \langle \mathbf{w}, \phi(\mathbf{x}, \mathbf{y}) \rangle - \langle \mathbf{w}, \phi(\mathbf{x}, \mathbf{t}) \rangle \\ & = \max_{y \in \mathcal{Y}} \left( \Delta(\mathbf{y}, \mathbf{t} + \langle \mathbf{w}, \phi(\mathbf{x}, \mathbf{y}) \rangle) \right) - \langle \mathbf{w}, \phi(\mathbf{x}, \mathbf{t}) \rangle\end{align}$

Optimization[edit]

The hinge loss is a convex function, so many of the usual convex optimizers used in machine learning can work with it. It is not differentiable, but has asubgradient with respect to model parameters 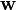$\mathbf{w}$ of a linear SVM with score function 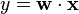$y = \mathbf{w} \cdot \mathbf{x}$ that is given by

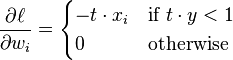
$\frac{\partial\ell}{\partial w_i} = \begin{cases} -t \cdot x_i & \text{if } t \cdot y < 1 \\ 0 & \text{otherwise} \end{cases}$

https://groups.google.com/forum/#!topic/theano-users/Y8lQqOzXC0A

由于hinge loss不是处处可导的。

Quick question: since hinge loss isn't differentiable, are there any standard practices / suggestions on how to implement a loss function
that might incorporate a max{0,something} in theano that can still be automatically differentiable? I'm thinking maybe evaluate a scalar
cost on the penultimate layer of the network and *hack* a loss function to arrive at a scalar loss?

I know of two differentiable functions that approximate the behavior
of max{0,x}. One is:

{log(1 + e^(x*N)) / N} -> max{0,x} as N->inf

The other is the activation function Geoff Hinton uses for rectified
linear units.

As a side note, in case anyone is curious where the crossover is:

log(1 + e^(x)) is the anti-derivative of the logistic function,
whereas RLUs are a form of integration that when carried out
infinitely will asymptotically approach the same behavior as log(1 +
e^(x)). That's the link between them.

-Brian

Thanks Brian, I actually ended up switching to a log-loss...

log(1 + exp( (m - x) * N)) / (m * N)

as an approximation to the margin loss I wanted,

max(0, m - x)

and everything's looking good / behaving nicely.

-Eric