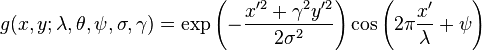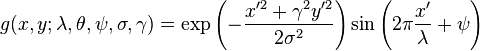Gabor filter

来源：互联网发布：手机淘宝个人主页标签编辑：程序博客网时间：2024/06/04 18:31

Gabor filter

From Wikipedia, the free encyclopedia

Example of a two-dimensional Gabor filter

In image processing, a Gabor filter, named after Dennis Gabor, is a linear filter used for edge detection. Frequency and orientation representations of Gabor filters are similar to those of the human visual system, and they have been found to be particularly appropriate for texture representation and discrimination. In the spatial domain, a 2D Gabor filter is a Gaussian kernel function modulated by a sinusoidal plane wave.

J. G. Daugman discovered that simple cells in the visual cortex of mammalian brains can be modeled by Gabor functions.^[1] Thus, image analysis by the Gabor functions is similar to perception in the human visual system.

[hide]

1 Definition
2 Feature extraction
3 Wavelet space
4 Example implementation
5 See also
6 References
7 External links
8 Further reading

Definition[edit]

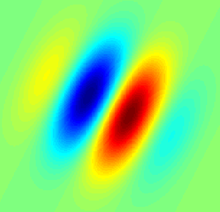
This section's factual accuracy is disputed.(February 2013)

Its impulse response is defined by a sinusoidal wave (a plane wave for 2D Gabor filters) multiplied by a Gaussian function.^[2] Because of the multiplication-convolution property (Convolution theorem), the Fourier transform of a Gabor filter's impulse response is the convolution of the Fourier transform of the harmonic function and the Fourier transform of the Gaussian function. The filter has a real and an imaginary component representing orthogonal directions.^[3] The two components may be formed into acomplex number or used individually.

Complex

$g(x,y;\lambda,\theta,\psi,\sigma,\gamma) = \exp\left(-\frac{x'^2+\gamma^2y'^2}{2\sigma^2}\right)\exp\left(i\left(2\pi\frac{x'}{\lambda}+\psi\right)\right)$

Real

$g(x,y;\lambda,\theta,\psi,\sigma,\gamma) = \exp\left(-\frac{x'^2+\gamma^2y'^2}{2\sigma^2}\right)\cos\left(2\pi\frac{x'}{\lambda}+\psi\right)$

Imaginary

$g(x,y;\lambda,\theta,\psi,\sigma,\gamma) = \exp\left(-\frac{x'^2+\gamma^2y'^2}{2\sigma^2}\right)\sin\left(2\pi\frac{x'}{\lambda}+\psi\right)$

where

$x' = x \cos\theta + y \sin\theta\,$

and

$y' = -x \sin\theta + y \cos\theta\,$

In this equation, $\lambda$ represents the wavelength of the sinusoidal factor, $\theta$ represents the orientation of the normal to the parallel stripes of a Gabor function, $\psi$ is the phase offset, $\sigma$ is the sigma/standard deviation of the Gaussian envelope and $\gamma$ is the spatial aspect ratio, and specifies the ellipticity of the support of the Gabor function.

Feature extraction[edit]

A set of Gabor filters with different frequencies and orientations may be helpful for extracting useful features from an image.

Wavelet space[edit]

Demonstration of a Gabor filter applied to Chinese OCR. Four orientations are shown on the right 0°, 45°, 90° and 135°. The original character picture and the superposition of all four orientations are shown on the left.

Gabor filters are directly related to Gabor wavelets, since they can be designed for a number of dilations and rotations. However, in general, expansion is not applied for Gabor wavelets, since this requires computation of bi-orthogonal wavelets, which may be very time-consuming. Therefore, usually, a filter bank consisting of Gabor filters with various scales and rotations is created. The filters are convolved with the signal, resulting in a so-called Gabor space. This process is closely related to processes in the primary visual cortex.^[4] Jones and Palmer showed that the real part of the complex Gabor function is a good fit to the receptive field weight functions found in simple cells in a cat's striate cortex.^[5]

The Gabor space is very useful in image processing applications such as optical character recognition, iris recognition and fingerprint recognition. Relations between activations for a specific spatial location are very distinctive between objects in an image. Furthermore, important activations can be extracted from the Gabor space in order to create a sparse object representation.

Example implementation[edit]

This is an example implementation in MATLAB/Octave:

function gb=gabor_fn(sigma,theta,lambda,psi,gamma) sigma_x = sigma;sigma_y = sigma/gamma; % Bounding boxnstds = 3;xmax = max(abs(nstds*sigma_x*cos(theta)),abs(nstds*sigma_y*sin(theta)));xmax = ceil(max(1,xmax));ymax = max(abs(nstds*sigma_x*sin(theta)),abs(nstds*sigma_y*cos(theta)));ymax = ceil(max(1,ymax));xmin = -xmax; ymin = -ymax;[x,y] = meshgrid(xmin:xmax,ymin:ymax); % Rotation x_theta=x*cos(theta)+y*sin(theta);y_theta=-x*sin(theta)+y*cos(theta); gb= exp(-.5*(x_theta.^2/sigma_x^2+y_theta.^2/sigma_y^2)).*cos(2*pi/lambda*x_theta+psi);

References[edit]

Jump up^ J. G. Daugman. Uncertainty relation for resolution in space, spatial frequency, and orientation optimized by two-dimensional visual cortical filters. Journal of the Optical Society of America A, 2(7):1160–1169, July 1985.
Jump up^ Fogel, I.; Sagi, D. (1989). "Gabor filters as texture discriminator". Biological Cybernetics 61 (2). doi:10.1007/BF00204594. ISSN 0340-1200.
Jump up^ 3D surface tracking and approximation using Gabor filters, Jesper Juul Henriksen, South Denmark University, March 28, 2007
Jump up^ Daugman, J.G. (1980), "Two-dimensional spectral analysis of cortical receptive field profiles", Vision Res. 20 (10): 847–56, PMID 7467139
Jump up^ J.P. Jones and L.A. Palmer. An evaluation of the two-dimensional gabor filter model of simple receptive fields in cat striate cortex. J. Neurophysiol., 58(6):1233-1258, 1987

External links[edit]

3D Gabor demonstrated with Mathematica
NuHAG homepage
Jesper Juul Henriksen Thesis

Gabor filter

Gabor filter

Contents

Definition[edit]

Feature extraction[edit]

Wavelet space[edit]

Example implementation[edit]

See also[edit]

References[edit]

External links[edit]

Further reading[edit]