POJ 1423 Big Number 解题报告

 

还以为是普通的高精度，结果Time Limit Exceed了。

one integer 1 <= m <= 10^7 on each line. 这个数量级不可能AC了。

#include<stdio.h>
#define MAX 100
int main()
{
    int n, m, i, j, base, set;
    int a[MAX];
    scanf("%d", &n);
    while(n--)
    {
        scanf("%d", &m);
        base = m;
        memset(a, 0, sizeof(a));
        for(i=0; base>0; i++, base /= 10)
            a[i] = base % 10;
        for(i=m-1; i>=1; i--)
        {
            set = 0;
            for(j=0; j<MAX; j++)
            {
                set = a[j] * i + set;
                a[j] = set % 10;
                set /= 10;
            }
        }
        for(i=MAX-1; i>=0; i--)
        {
            if(a[i] != 0)
                break;
        }
        printf("%d/n", i+1);
    }
    return 0;
}

 

看了Discuss，基本上有两种方法：

1。用Stirling公式

公式和证明如下：

An important formula in applied mathematics as well as in probability is the Stirling's formula known as

 

 

where is used to indicate that the ratio of the two sides goes to 1 as n goes to . In other words, we have

 

 

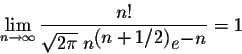
or

 

 

 

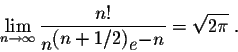
Proof of the Stirling's Formula

First take the log of n! to get

 

 

Since the log function is increasing on the interval , we get

 

 

for . Add the above inequalities, with , we get

 

 

Though the first integral is improper, it is easy to show that in fact it is convergent. Using the antiderivative of (being ), we get

 

 

Next, set

 

 

We have

 

 

Easy algebraic manipulation gives

 

 

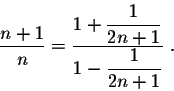
Using the Taylor expansion

 

 

for -1 < t < 1, we get

 

 

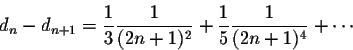
This implies

 

 

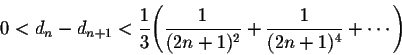
We recognize a geometric series. Therefore we have

 

 

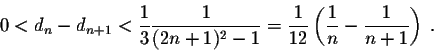
From this we get

1.

the sequence 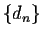is decreasing;

2.

the sequence 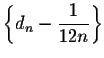is increasing.

This will imply that converges to a number C with

 

 

and that C > d₁ - 1/12 = 1 - 1/12 = 11/12. Taking the exponential of d_n, we get

 

 

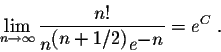
The final step in the proof if to show that . This will be done via Wallis formula (and Wallis integrals). Indeed, recall the limit

 

 

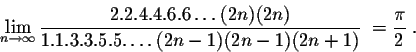
Rewriting this formula, we get

 

 

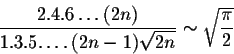
Playing with the numbers, we get

 

 

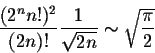
Using the above formula

 

 

we get

 

 

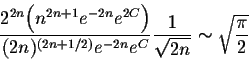
Easy algebra gives

 

 

since we are dealing with constants, we get in fact . This completes the proof of the Stirling's formula.

AC code：

#include <stdio.h>
#include <math.h>

int n;
const double e = 2.7182818284590452354, pi = 3.141592653589793239;

double f( int a )
{
    return log10( sqrt( 2 * pi * a ) ) + a * log10( a / e );
}

int main()
{
    int cas, ans;
    double i, s;
    
    scanf( "%d", &cas );
    
    while( cas-- )
    {
        scanf( "%d", &n );
        if( n < 100000 )
        {
            for( s=0, i=1; i<=n; i++ )
                s += log10( i );
        }
        else s = f( n );
        ans = (int)s;
        if( ans <= s )
            ans++;
        
        printf( "%d/n", ans );
    }
    
    return 0;
}

 

2。用 位数=[ lg1+lg2+……lg(N-1)+lgN ] + 1。

数很大时，速度会慢，TLE。。

所以如上述AC代码，小于100000时，可以用这种方法，再大的话最好用Stiring公式。