EM（理论）

在讲EM算法之前，我们先从一个例子开始。例如，我们随机抽取了400个人的身高，如果男生为200人，我们可以单独得到一个分布，而女生为200人，也可以同样得到一个分布（假设身高服从高斯分布），如图1。

图1 男生和女生各自的分布直方图（男和女没有混合）

图2 男女混合后的分布直方图

   假如，分开来计算分布的参数的话，可以使用最大似然估计来估计。现在我们将抽取的这400人混合在一起，来进行统计，如图2所示，那我们如何估计统计模型的参数呢？而这个统计模型是什么呢？(这个好像需要我们自己去假设，这个需要我们通过统计来观察直方图)从图2看，400人的身高的统计直方图(感觉应该是xx模型（分布）的某种组合，线性的？或是非线性的？），这里我们可以构造一个高斯混合模型，然后使用样本（400个数据样例），利用最大似然来估计模型的参数（好像数理统计是从数据出发，来研究数据之间的概率模型（一种数学模型））。

  在运用最大似然估计，估计高斯混合模型的参数的时候，遇到了困难（求导很困难）（见高斯混合模型GMM（理论）），因此我们需要使用EM算法来求解（这么说来，EM这个算法的作用是：相当于绕过了这个困难，达到了同样使高斯混合模型的似然函数达到最优的值，擦，这不是和什么牛顿法，梯度下降法之类的算法功能一样？事实上就是这样的，本质上EM算法也是一种最优算法，相当于坐标上升法（Coordinate ascent），至于为什么，下面在解释）。

  下面我们开始讲EM算法。

   EM算法意思是“Expectation Maximization”。那它为什么要取这样的名字呢？那肯定是有原因的，比如有一个叫BP的算法，之所以这样命名，是和它算法本身的特点有关的，同样的道理EM算法为什么这样命名，同样和它的算法特点有关。不过如何我们先说一下这种算法的基本思想：对于相互依赖的问题，如先有鸡还是先有蛋的问题，为了解决这种你依赖我，我依赖你的循环依赖问题，我们可以先假设一方的值知道了，接着看另外一方的值怎么变，然后我再根据你的变化调整我的变化，然后如此迭代着不断互相推导，最终就会收敛到一个解。

EM的算法流程：

    给定的训练样本是

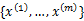
，样例间独立，我们想找到每个样例隐含的类别z（比如在上面的例子中，从400人的身高中随便挑一个出来，它可能属于男生身高这个分布，也可属于女生身高的那个分布。我们可以假设z=0，为属于男生的分布，z=1，为属于女生的分布，x表示身高(1维)），能使得p(x,z)最大。p(x,z)的最大似然估计如下： 

 

    由于这里，我们假设x只是一个维度（如身高），并且假设服从高斯分布，那么对于z=0（男生身高分布）和z=1（女生身高分布）的情况，它们对应的概率密度函数为：

由此，可以假设参数

，实际上： 

 

 

但是现在的问题又来了，因为要估计使得

最大的参数θ，自然我们会想到对参数θ的各个分量求偏导数即可，可是诸如log(f1+f2+...)类型的函数，求倒数很困难。既然有困难就要想办法，惰性使然（好像人类的文明进步都是由于人类固有的惰性哦），人们在思考，可不可以通过其他的、相对容易的、有可以达到同样目的的方法呢？于是人们想到了EM算法，来使得似然函数达到最优值。 

EM是一种解决存在隐含变量优化问题的有效方法。既然不能直接最大化

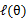
，我们可以不断地建立 

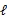
的下界（E步），然后优化下界（M步）。这句话比较抽象，看下面的。 

      对于每一个样例i（比如张三(第i个抽样对象)的身高为1.81m)，让

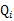
表示该样例隐含变量z（类别：男生身高分布，女生身高分布）的某种分布（概率）(z=0，表示张三身高属于男生那个分布，z=1表示张三身高属于是女生的那个分布，也就是说 

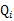
(z=0)，表示张三属于男生身高分布的概率， 

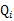
(z=1)表示张三属于女生身高分布的概率)， 

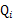
满足的条件是 

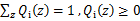
。（如果z是连续性的，那么 

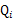
是概率密度函数，需要将求和符号换做积分符号）。比如要将班上学生聚类，假设隐藏变量z是身高，那么就是连续的高斯分布。如果按照隐藏变量是男女，那么就是伯努利分布了。 

可以由前面阐述的内容得到下面的公式：

      

      （1）到（2）比较直接，就是分子分母同乘以一个相等的函数。（2）到（3）利用了Jensen不等式(其实就是因为似然函数求导难，因此将它进行变形转换（在别处容易求），从而达到求解最大值的目的)，考虑到

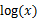
是凹函数（二阶导数小于0），而且 

      

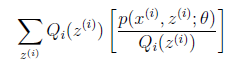
      就是

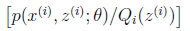
的期望（回想期望公式中的Lazy Statistician规则） 

 

  对应于上述问题，Y是

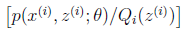
，X是 

， 

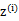
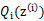
是 

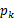
，g是 

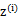
到 

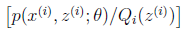
的映射。这样解释了式子（2）中的期望，再根据凹函数时的Jensen不等式： 

      

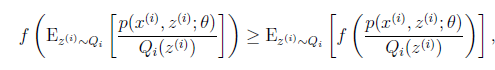
可以得到（3）。

      这个过程可以看作是对

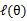
求了下界。对于 

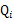
的选择，有多种可能，那种更好的？假设 

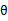
已经给定（这句话很关键，打破鸡生蛋蛋生鸡问题循环的僵局），那么 

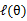
的值就决定于 

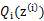
和 

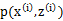
了。我们可以通过调整这两个概率使下界不断上升，以逼近 

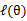
的真实值，那么什么时候算是调整好了呢？当不等式变成等式（=）时，说明我们调整后的概率能够等价于 

了。按照这个思路，我们要找到等式成立的条件。根据Jensen不等式，要想让等式成立，需要让随机变量变成常数值，这里得到： 

      

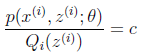
      c为常数，不依赖于

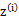
。对此式子做进一步推导，我们知道 

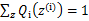
，那么也就有 

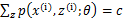
（为什么这样，拿起笔计算），（多个等式分子分母相加不变，这个认为每个样例的两个概率比值都是c），那么有下式： 

      

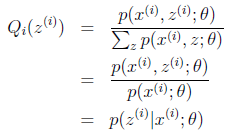
      至此，我们推出了在固定其他参数

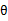
后， 

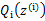
的计算公式就是 后验概率（已知θ的情况下，x属于z类别的概率），从求 

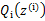
式子来看（比如某个身高值(1.81m)，它属于男生身高分布(z=0)是的概率是p1，它属于女生身高分布的概率是p2, 

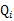
(z=0)是等于p1/(p1+p2)， 

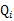
(z=1)是等于p2/(p1+p2)，这不是把p1和p2个平均化吗？注意到了平均（Expectation），之外注意p1+p2不等于1，这个地方不好理解），解决了 

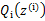
如何选择的问题。这一步就是E步，建立 

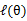
的下界。接下来的M步，就是在给定 

后，调整 

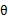
，去极大化 

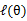
的下界（在固定 

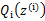
后，下界还可以调整的更大）。那么一般的EM算法的步骤如下： 

    （1）初始化分布参数θ；

 

    （2）重复以下步骤直到收敛：

        E步骤：根据参数初始值或上一次迭代的模型参数来计算出隐性变量(z)的后验概率，其实就是隐性变量的期望（Expectation）。作为隐藏变量的现估计值：

       

        M步骤：将似然函数最大化（Maximization）以获得新的参数值：

          

        这个不断的迭代，就可以得到使似然函数L(θ)最大化的参数θ了。那这样子迭代下去，它会收敛吗？

    假定

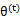
和 

是EM第t次和t+1次迭代后的结果。如果我们证明了 

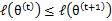
，也就是说极大似然估计单调增加，那么最终我们会到达最大似然估计的最大值。下面来证明，选定 

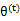
后，我们得到E步 

      

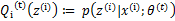
      这一步保证了在给定

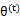
时，Jensen不等式中的等式成立，也就是 

      

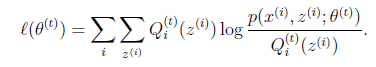
      然后进行M步，固定

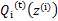
，并将 

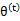
视作变量，对上面的 

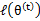
求导后，得到 

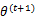
，这样经过一些推导会有以下式子成立： 

      

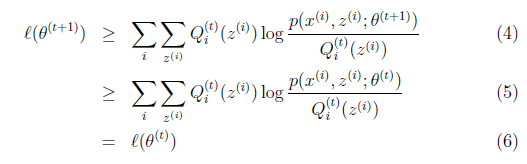
      解释第（4）步，得到

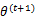
时，只是最大化 

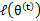
，也就是 

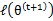
的下界，而没有使等式成立，等式成立只有是在固定 

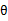
，并按E步得到 

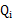
时才能成立。 

      况且根据我们前面得到的下式，对于所有的

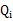
和 

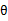
都成立 

      

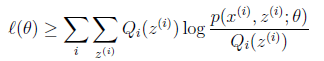
      第（5）步利用了M步的定义，M步就是将

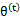
调整到 

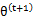
，使得下界最大化。因此（5）成立，（6）是之前的等式结果。 

      这样就证明了

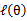
会单调增加。一种收敛方法是 

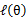
不再变化，还有一种就是变化幅度很小。 

      再次解释一下（4）、（5）、（6）。首先（4）对所有的参数都满足，而其等式成立条件只是在固定

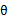
，并调整好Q时成立，而第（4）步只是固定Q，调整 

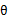
，不能保证等式一定成立。（4）到（5）就是M步的定义，（5）到（6）是前面E步所保证等式成立条件。也就是说E步会将下界拉到与 

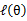
一个特定值（这里 

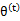
）一样的高度，而此时发现下界仍然可以上升，因此经过M步后，下界又被拉升，但达不到与 

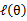
另外一个特定值一样的高度，之后E步又将下界拉到与这个特定值一样的高度，重复下去，直到最大值。 

      如果我们定义

      

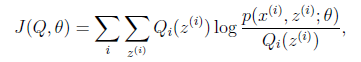
      从前面的推导中我们知道

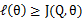
，EM可以看作是J的坐标上升法，E步固定 

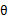
，优化 

，M步固定 

优化 

。 

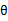
     混合高斯模型的审视：

     我们已经知道了EM的精髓和推导过程，再次审视一下混合高斯模型。假设混合高斯模型的参数为

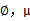
和 

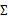
，还有混合高斯模型的计算公式都是根据很多假定得出的，有些没有说明来由。为了简单，这里在M步只给出 

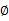
（加权系数）和 

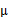
（均值）的推导方法。 

E步很简单，按照一般EM公式得到：

      

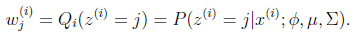
      简单解释就是每个样例i的隐含类别

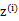
为j（如上面的例子,j的取值0,1)的概率可以通过后验概率计算得到。 

      在M步中，我们需要在固定

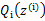
后最大化最大似然估计，也就是 

      

      这是将

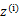
的k种情况展开后的样子，未知参数 

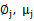
和 

。 

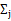
      固定

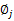
（加权系数）和 

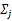
（协方差矩阵，在1元高斯时，是方差），对 

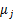
（均值）求偏导数得 

      

      等于0时，得到

      

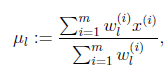
      这就是我们高斯混合模型中的

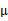
的更新公式。 

      然后推导

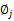
（加权系数）的更新公式。看之前得到的 

      

      在

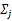
和 

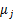
确定后，分子上面的一串都是常数了，实际上需要优化的公式是： 

      

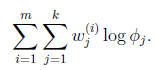
      需要知道的是，

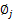
还需要满足一定的约束条件就是 

。 

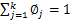
      这个优化问题我们很熟悉了，直接构造拉格朗日乘子。

      

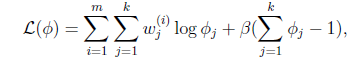
      还有一点就是

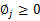
，但这一点会在得到的公式里自动满足。 

      求偏导数得，

      

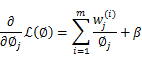
      等于0，得到

      

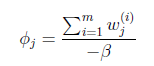
      也就是说

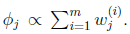
再次使用 

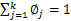
，得到 

      

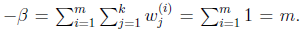
      这样就神奇地得到了

。 

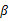
      那么就顺势得到M步中

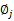
的更新公式： 

      

      

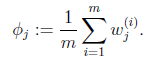
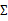
的推导也类似，不过稍微复杂一些，毕竟是矩阵。结果在 混合高斯模型中已经给出。 

      如果将样本看作观察值（身高），潜在类别看作是隐藏变量，那么聚类问题也就是参数估计问题，只不过聚类问题中参数分为隐含类别变量和其他参数，这犹如在x-y坐标系中找一个曲线的极值，然而曲线函数不能直接求导，因此什么梯度下降方法就不适用了。但固定一个变量后，另外一个可以通过求导得到，因此可以使用坐标上升法，一次固定一个变量，对另外的求极值，最后逐步逼近极值。对应到EM上，E步估计隐含变量（类别，样本在各个分布（2个分布,就是2类）的概率），M步估计其他参数，交替将极值推向最大。EM中还有“硬”指定和“软”指定的概念，“软”指定看似更为合理，但计算量要大，“硬”指定在某些场合如K-means中更为实用（要是保持一个样本点到其他所有中心的概率，就会很麻烦）。

      另外，EM的收敛性证明方法确实很牛，能够利用log的凹函数性质，还能够想到利用创造下界，拉平函数下界，优化下界的方法来逐步逼近极大值。而且每一步迭代都能保证是单调的。最重要的是证明的数学公式非常精妙，硬是分子分母都乘以z的概率变成期望来套上Jensen不等式，前人都是怎么想到的。

      在Mitchell的Machine Learning书中也举了一个EM应用的例子，明白地说就是将班上学生的身高都放在一起，要求聚成两个类。这些身高可以看作是男生身高的高斯分布和女生身高的高斯分布组成。因此变成了如何估计每个样例是男生还是女生，然后在确定男女生情况下，如何估计均值和方差，里面也给出了公式，有兴趣可以参考。

 
 

 
 

 

参考文献：

1.从最大似然到EM算法浅解

2.（EM算法）The EM Algorithm