求最远点对

来源：互联网发布：北京网络公关公司编辑：程序博客网时间：2024/05/17 23:28

问题（编程之美）
给定平面上N个点的坐标，找出距离最远的两个点。
分析
类似于“最近点对问题”，这个问题也可以用枚举的方法求解，时间复杂度O(n^2)。
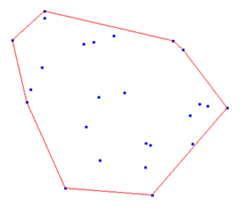
“寻找最近点对”是用到分治策略降低复杂度，而“寻找最远点对”可利用几何性质。注意到：对于平面上有n个点，这一对最远点必然存在于这n个点所构成的一个凸包上（证明略），那么可以排除大量点，如下图所示：

在得到凸包以后，可以只在顶点上面找最远点了。同样，如果不O(n^2)两两枚举，可以想象有两条平行线， “卡”住这个凸包，然后卡紧的情况下旋转一圈，肯定就能找到凸包直径，也就找到了最远的点对。或许这就是为啥叫“旋转卡壳法”。

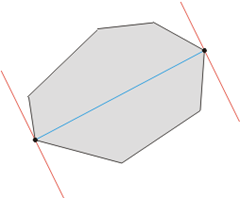
总结起来，问题解决步骤为：
1、用Graham's Scanning求凸包
2、用Rotating Calipers求凸包直径，也就找到了最远点对。
该算法的平均复杂度为O(nlogn) 。最坏的情况下，如果这n个点本身就构成了一个凸包，时间复杂度为O(n^2)。
旋转卡壳可以用于求凸包的直径、宽度，两个不相交凸包间的最大距离和最小距离等。虽然算法的思想不难理解，但是实现起来真的很容易让人“卡壳”。

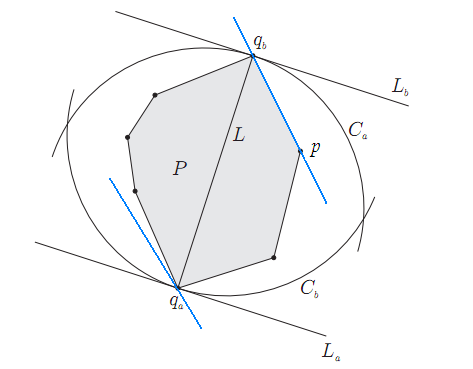
逆向思考，如果qa，qb是凸包上最远两点，必然可以分别过qa，qb画出一对平行线。通过旋转这对平行线，我们可以让它和凸包上的一条边重合,如图中蓝色直线，可以注意到，qa是凸包上离p和qb所在直线最远的点。于是我们的思路就是枚举凸包上的所有边，对每一条边找出凸包上离该边最远的顶点，计算这个顶点到该边两个端点的距离，并记录最大的值。直观上这是一个O(n2)的算法，和直接枚举任意两个顶点一样了。但是注意到当我们逆时针枚举边的时候，最远点的变化也是逆时针的，这样就可以不用从头计算最远点，而可以紧接着上一次的最远点继续计算，于是我们得到了O(n)的算法。

http://poj.org/problem?id=2187

[cpp] view plaincopy
// 求最远点对  
#include<iostream>  
#include<algorithm>  
using namespace std;  
  
struct point  
{  
    int x , y;  
}p[50005];  
  
int top , stack[50005];    // 凸包的点存在于stack[]中  
  
inline double dis(const point &a , const point &b)  
{  
    return (a.x - b.x)*(a.x - b.x)+(a.y - b.y)*(a.y - b.y);  
}  
inline int max(int a , int b)  
{  
    return a > b ? a : b;  
}  
inline int xmult(const point &p1 , const point &p2 , const point &p0)  
{   //计算叉乘--线段旋转方向和对应的四边形的面积--返回(p1-p0)*(p2-p0)叉积  
    //if叉积为正--p0p1在p0p2的顺时针方向; if(x==0)共线  
    return (p1.x-p0.x)*(p2.y-p0.y) - (p1.y-p0.y)*(p2.x-p0.x);  
}  
  
int cmp(const void * a , const void * b) //逆时针排序 返回正数要交换  
{  
    struct point *p1 = (struct point *)a;  
    struct point *p2 = (struct point *)b;  
    int ans = xmult(*p1 , *p2 , p[0]);   //向量叉乘  
    if(ans < 0)   //p0p1线段在p0p2线段的上方，需要交换  
        return 1;  
    else if(ans == 0 && ( (*p1).x >= (*p2).x))     //斜率相等时，距离近的点在先  
        return 1;  
    else  
        return -1;  
}  
void graham(int n) //形成凸包  
{  
    qsort(p+1 , n-1 , sizeof(point) , cmp);  
    int i;  
    stack[0] = 0 , stack[1] = 1;  
    top = 1;  
    for(i = 2 ; i < n ; ++i)  
    {  
        while(top > 0 && xmult( p[stack[top]] , p[i] , p[stack[top-1]]) <= 0)  
            top--;           //顺时针方向--删除栈顶元素  
        stack[++top] = i;    //新元素入栈  
    }  
    int temp = top;  
    for(i = n-2 ; i >= 0 ; --i)  
    {  
        while(top > temp && xmult(p[stack[top]] , p[i] , p[stack[top-1]]) <= 0)  
            top--;  
        stack[++top] = i;    //新元素入栈  
    }  
}  
int rotating_calipers()  //卡壳  
{  
    int i , q=1;  
    int ans = 0;  
    stack[top]=0;  
    for(i = 0 ; i < top ; i++)  
    {  
        while( xmult( p[stack[i+1]] , p[stack[q+1]] , p[stack[i]] ) > xmult( p[stack[i+1]] , p[stack[q]] , p[stack[i]] ) )  
            q = (q+1)%(top);  
        ans = max(ans , max( dis(p[stack[i]] , p[stack[q]]) , dis(p[stack[i+1]] , p[stack[q+1]])));  
    }  
    return ans;  
}  
  
int main(void)  
{  
    int i , n , leftdown;   
    while(scanf("%d",&n) != EOF)  
    {  
        leftdown = 0;  
        for(i = 0 ; i < n ; ++i)  
        {  
            scanf("%d %d",&p[i].x,&p[i].y);  
            if(p[i].y < p[leftdown].y || (p[i].y == p[leftdown].y && p[i].x < p[leftdown].x))  //找到最左下角的点  
                leftdown = i;  
        }  
        swap(p[0] , p[leftdown]);  
        graham(n);  
        printf("%d\n",rotating_calipers());    
    }  
    return 0;  
}  

也看看http://www.cnblogs.com/Booble/archive/2011/03/10/1980089.html

0 0