《Thinking In Algorithm》07.Red-Black Trees（红黑树）

一：红黑树简介

红黑树，一种二叉查找树，但在每个结点上增加一个存储位表示结点的颜色，可以是Red或Black。
通过对任何一条从根到叶子的路径上各个结点着色方式的限制，红黑树确保没有一条路径会比其他路径长出俩倍，因而是接近平衡的。

上面我们知道了，红黑树是二叉查找树的一种，所以首先要满足二叉查找树的性质，前面的博客Binary search trees中我们详细介绍了二叉查找树。

回顾一下：

• The left subtree of a node contains only nodes with keys less than the node's key.
• The right subtree of a node contains only nodes with keys greater than the node's key.
• The left and right subtree each must also be a binary search tree.
• There must be no duplicate nodes.

我们知道二叉查找树的时间复杂度为O(h)，所以当树的高度很大时，对二叉树的操作可能能还不如链表。

而 红黑树，能保证在最坏情况下，基本的动态几何操作的时间均为O（lgn）。

Each node of the tree now contains the attributes color, key, left, right, and p.

红黑树的性质：

• 1. Every node is either red or black.
• 2. The root is black.
• 3. Every leaf (NIL) is black.
• 4. If a node is red, then both its children are black.
• 5. For each node, all simple paths from the node to descendant leaves contain the same number of black nodes.

下面是红黑树的例子

二：树的旋转

在对红黑树的插入和删除进行详解之前，我们不得不先提下树的旋转，回忆下在二叉查找树中我们对元素删除和插入花费时间为O(h)，而在红黑树中却为O(lgn)，这是因为在经过二叉查找树的那些操作后，红黑树为了保证其特有性质必须进行树的旋转。

树的旋转分为左旋和右旋如下图：

左旋的伪代码：LEFT-ROTATE(T,x)

y = x.right//set yx.right = y.left//turn y's left subtree into x's right subtreeif y.left != T.nily.left.p = xy.p = x.p//link x's parent to yif x.p == T.nilT.root = yelseif x == x.p.leftx.p.left = yelse x.p.right = yy.left = x//put x on y's leftx.p = y

三：红黑树的插入操作

红黑树的插入操作时间里在二叉查找树的插入操作的基础上多了几步。先看伪代码。

从伪代码中，我们对比前面讲过的二叉查找树插入操作的伪代码，可以看出多出了14-17行的代码。1-13行都是一样的。

14-16行我们就不详细解释了，就是假设插入元素z的颜色为RED且插入后两孩子为nil。

对于RB-INSERT-FIXUP(T,z)操作，因为插入后的元素虽然满足了二叉查找树的特性但不满足红黑树的特性，所以要进行RB-INSERT-FIXUP(T,z)操作

我们首先回顾下红黑树的特性：

• 1）每个结点要么是红的，要么是黑的。
• 2）根结点是黑的。
• 3）每个叶结点，即空结点（NIL）是黑的。
• 4）如果一个结点是红的，那么它的俩个儿子都是黑的。
• 5）对每个结点，从该结点到其子孙结点的所有路径上包含相同数目的黑结点。

我们下面给出其源码：

在wikipedia上把插入后分为五种情况，算法导论中只分为1,2,3中情况分别对应wiki上的3,4,5

以wikipedia上的为例：

下面各情况可能调用的代码：

struct node *grandparent(struct node *n){ if ((n != NULL) && (n->parent != NULL))  return n->parent->parent; else  return NULL;} struct node *uncle(struct node *n){ struct node *g = grandparent(n); if (g == NULL)  return NULL; // No grandparent means no uncle if (n->parent == g->left)  return g->right; else  return g->left;}

Case 1：当前节点z是树的根节点，因为z是红色的不满足属性2（根节点为黑），所以只需要吧节点颜色变为黑

void insert_case1(struct node *n){ if (n->parent == NULL)  n->color = BLACK; else  insert_case2(n);}

Case 2：节点z的父节点是黑色的，此时没有违背任何特性所以不需要做任何操作。

void insert_case2(struct node *n){ if (n->parent->color == BLACK)  return; /* Tree is still valid */ else  insert_case3(n);}

Case 3：如果z的父节点p和叔叔节点U都是红色的。 那么此时违背了特性4（红色节点有两个黑孩子，而z是红色）。所以要把p和u改为黑色，祖父改为红色

c代码：

void insert_case3(struct node *n){ struct node *u = uncle(n), *g;  if ((u != NULL) && (u->color == RED)) {  n->parent->color = BLACK;  u->color = BLACK;  g = grandparent(n);  g->color = RED;  insert_case1(g);                            //确保g节点不会违背属性2 } else {  insert_case4(n); }}

Case 4：父节点p是红色，而叔叔节点是黑色，且z节点是p的右孩子。此时依然违背属性4.要进行左旋。进行左旋之后你会发现还是违背，所以要进行案例5了，案例4这样做的目的就是转成案例5.

c代码：

void insert_case4(struct node *n){ struct node *g = grandparent(n);  if ((n == n->parent->right) && (n->parent == g->left)) {  rotate_left(n->parent);  /* * rotate_left can be the below because of already having *g =  grandparent(n)  * * struct node *saved_p=g->left, *saved_left_n=n->left; * g->left=n;  * n->left=saved_p; * saved_p->right=saved_left_n; *  * and modify the parent's nodes properly */   n = n->left;   } else if ((n == n->parent->left) && (n->parent == g->right)) {  rotate_right(n->parent);  /* * rotate_right can be the below to take advantage of already having *g =  grandparent(n)  * * struct node *saved_p=g->right, *saved_right_n=n->right; * g->right=n;  * n->right=saved_p; * saved_p->left=saved_right_n; *  */   n = n->right;  } insert_case5(n);}

Case 5：父节点p是红，叔叔节点U是黑，且z是p的左孩子。此时违背属性4，先进行右旋，在改色。如下图

c代码

void insert_case5(struct node *n){ struct node *g = grandparent(n);  n->parent->color = BLACK; g->color = RED; if (n == n->parent->left)  rotate_right(g); else  rotate_left(g);}

四：红黑树的删除

红黑树的删除也是必须先保证其二叉查找树，然后确保红黑树的性质。

上面的操作跟二叉搜索树差不多，下面的伪代码是对其红黑树性质修复。

下面对其中四中情况进行讨论

• 情况1：x的兄弟w是红色的。
• 情况2：x的兄弟w是黑色的，且w的俩个孩子都是黑色的。
• 情况3：x的兄弟w是黑色的，w的左孩子是红色，w的右孩子是黑色。
• 情况4：x的兄弟w是黑色的，且w的右孩子时红色的。

对应的操作如下

ok，简单分析下，红黑树删除的4种情况：

针对情况1：x的兄弟w是红色的。

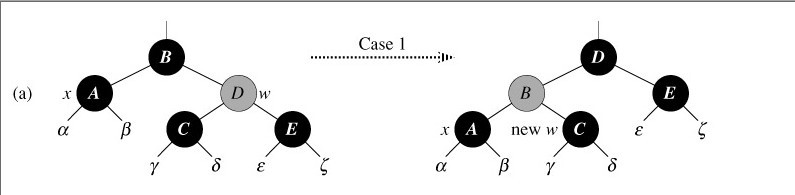
 5                   then color[w] ← BLACK                        ▹  Case 1
 6                        color[p[x]] ← RED                       ▹  Case 1
 7                        LEFT-ROTATE(T, p[x])                    ▹  Case 1
 8                        w ← right[p[x]]                         ▹  Case 1

对策：改变w、p[z]颜色，再对p[x]做一次左旋，红黑性质得以继续保持。

x的新兄弟new w是旋转之前w的某个孩子，为黑色。

所以，情况1转化成情况2或3、4。

 

针对情况2：x的兄弟w是黑色的，且w的俩个孩子都是黑色的。

10                   then color[w] ← RED                          ▹  Case 2
11                        x <-p[x]                                  ▹  Case 2
如图所示，w的俩个孩子都是黑色的，

对策：因为w也是黑色的，所以x和w中得去掉一黑色，最后，w变为红。

p[x]为新结点x，赋给x，x<-p[x]。

 

针对情况3：x的兄弟w是黑色的，w的左孩子是红色，w的右孩子是黑色。

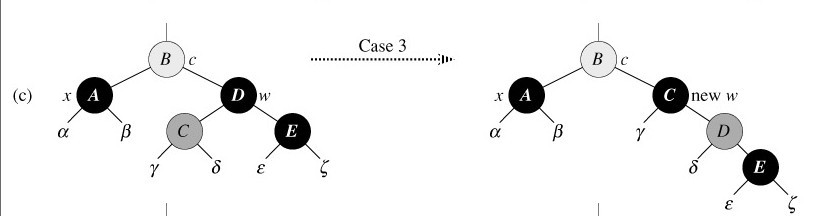
13                           then color[left[w]] ← BLACK          ▹  Case 3
14                                color[w] ← RED                  ▹  Case 3
15                                RIGHT-ROTATE(T, w)              ▹  Case 3
16                                w ← right[p[x]]                 ▹  Case 3
w为黑，其左孩子为红，右孩子为黑

对策：交换w和和其左孩子left[w]的颜色。 即上图的D、C颜色互换。:D。

并对w进行右旋，而红黑性质仍然得以保持。

现在x的新兄弟w是一个有红色右孩子的黑结点，于是将情况3转化为情况4.

 

针对情况4：x的兄弟w是黑色的，且w的右孩子时红色的。

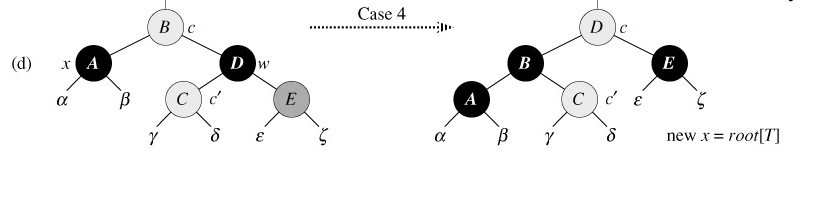
17                         color[w] ← color[p[x]]                 ▹  Case 4
18                         color[p[x]] ← BLACK                    ▹  Case 4
19                         color[right[w]] ← BLACK                ▹  Case 4
20                         LEFT-ROTATE(T, p[x])                   ▹  Case 4
21                         x ← root[T]                            ▹  Case 4
x的兄弟w为黑色，且w的右孩子为红色。

对策：做颜色修改，并对p[x]做一次旋转，可以去掉x的额外黑色，来把x变成单独的黑色，此举不破坏红黑性质。

将x置为根后，循环结束。

五：补充

排序二叉树虽然可以快速检索，但在最坏的情况下：如果插入的节点集本身就是有序的，要么是由小到大排列，要么是由大到小排列，那么最后得到的排序二叉树将变成链表：所有节点只有左节点（如果插入节点集本身是大到小排列）；或所有节点只有右节点（如果插入节点集本身是小到大排列）。在这种情况下，排序二叉树就变成了普通链表，其检索效率就会很差。

为了改变排序二叉树存在的不足，Rudolf Bayer 与 1972 年发明了另一种改进后的排序二叉树：红黑树，他将这种排序二叉树称为“对称二叉 B 树”，而红黑树这个名字则由 Leo J. Guibas 和 Robert Sedgewick 于 1978 年首次提出。

红黑树是一个更高效的检索二叉树，因此常常用来实现关联数组。典型地，JDK 提供的集合类 TreeMap 本身就是一个红黑树的实现。

红黑树在原有的排序二叉树增加了如下几个要求：

Java 实现的红黑树

上面的性质 3 中指定红黑树的每个叶子节点都是空节点，而且并叶子节点都是黑色。但 Java 实现的红黑树将使用 null 来代表空节点，因此遍历红黑树时将看不到黑色的叶子节点，反而看到每个叶子节点都是红色的。

• 性质 1：每个节点要么是红色，要么是黑色。
• 性质 2：根节点永远是黑色的。
• 性质 3：所有的叶节点都是空节点（即 null），并且是黑色的。
• 性质 4：每个红色节点的两个子节点都是黑色。（从每个叶子到根的路径上不会有两个连续的红色节点）
• 性质 5：从任一节点到其子树中每个叶子节点的路径都包含相同数量的黑色节点。

Java 中实现的红黑树可能有如图 6 所示结构：

图 6. Java 红黑树的示意

备注：本文中所有关于红黑树中的示意图采用白色代表红色。黑色节点还是采用了黑色表示。

根据性质 5：红黑树从根节点到每个叶子节点的路径都包含相同数量的黑色节点，因此从根节点到叶子节点的路径中包含的黑色节点数被称为树的“黑色高度（black-height）”。

性质 4 则保证了从根节点到叶子节点的最长路径的长度不会超过任何其他路径的两倍。假如有一棵黑色高度为 3 的红黑树：从根节点到叶节点的最短路径长度是 2，该路径上全是黑色节点（黑节点 - 黑节点 - 黑节点）。最长路径也只可能为 4，在每个黑色节点之间插入一个红色节点（黑节点 - 红节点 - 黑节点 - 红节点 - 黑节点），性质 4 保证绝不可能插入更多的红色节点。由此可见，红黑树中最长路径就是一条红黑交替的路径。

红黑树和平衡二叉树

红黑树并不是真正的平衡二叉树，但在实际应用中，红黑树的统计性能要高于平衡二叉树，但极端性能略差。

由此我们可以得出结论：对于给定的黑色高度为 N 的红黑树，从根到叶子节点的最短路径长度为 N-1，最长路径长度为 2 * (N-1)。

提示：排序二叉树的深度直接影响了检索的性能，正如前面指出，当插入节点本身就是由小到大排列时，排序二叉树将变成一个链表，这种排序二叉树的检索性能最低：N 个节点的二叉树深度就是 N-1。

红黑树通过上面这种限制来保证它大致是平衡的——因为红黑树的高度不会无限增高，这样保证红黑树在最坏情况下都是高效的，不会出现普通排序二叉树的情况。

由于红黑树只是一个特殊的排序二叉树，因此对红黑树上的只读操作与普通排序二叉树上的只读操作完全相同，只是红黑树保持了大致平衡，因此检索性能比排序二叉树要好很多。

但在红黑树上进行插入操作和删除操作会导致树不再符合红黑树的特征，因此插入操作和删除操作都需要进行一定的维护，以保证插入节点、删除节点后的树依然是红黑树。

References：

http://en.wikipedia.org/wiki/Red–black_tree

http://blog.csdn.net/v_july_v/article/details/6105630