Codeforces Round #236 (Div. 2) [ C题+D题+E题]

C

Searching for Graph

题：让你构造一个无向图 ， 满足这样的条件：

• the graph contains exactly 2n + p edges;
• the graph doesn't contain self-loops and multiple edges;
• for any integer k (1 ≤ k ≤ n), any subgraph consisting ofk vertices contains at most2k + p edges.

分析： 整个图有2n+p条边，每个子图边数<=2k+p ,  只要让边分布均匀， 避免局部边太密集即可。

一种方案：

#include <iostream>#include <cstdio>#include <cstring>#include <algorithm>using namespace std;bool used[50][50] ;int main(){    int T ;    cin>>T;    while(T--)    {        memset(used ,0 ,sizeof(used)) ;        int n , p ;        cin>>n>>p ;        p+=n ;        for(int i=1; i<n ;i++){            cout<<i<<" "<<i+1<<endl;            used[i][i+1] = used[i+1][i] = true ;        }        used[1][n] = used[n][1]=true ;        cout<<n<<" 1"<<endl ;        int now = 0 , len = 2 ;        int u ,v ;        while(p--){            u = now , v = (u+len) % n ;            u++ , v++;            bool flag = false ;            if(used[u][v]){                now=0 ; len++ ;                u = now , v = (u+len) % n ;                u++ , v++;                cout<<u<<" "<<v<<endl ;                flag = true ;            }            used[u][v] = used[v][u] = true ;            if(!flag) cout<<u<<" "<<v<<endl ;            now = (now+1)%n;        }    }    return 0;}

D题

Upgrading Array

：

不可不说这是个好题。
题意： 将素数分为bad prime 和 good prime.

定义权值 f函数为：

• f(1) = 0;
• Let's assume that p is the minimum prime divisor ofs. Ifp is a good prime, then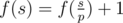, otherwise.

允许对数组a[]进行这样的操作：

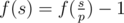• Choose some number r (1 ≤ r ≤ n) and calculate the valueg = GCD(a[1], a[2], ..., a[r]).
• Apply the assignments: ,,...,.

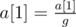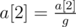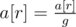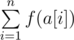问通过一些操作，权值之和 最大能达到多少？

分析： 设good prime为 P1 , P2 , P3 ....      ,  bad prime  为 Q1 , Q2 , Q3 , ......

将X分解为:  X = ( P1^a1  + P2^a2 + ..... + Pn^an)       +      (Q1^b1  + Q2^b2 + ....  Qm^bm)

则  f(X)  =  (a1+a2+...an)   -   (b1 + b2 + b3 ... bm)

易知:   f(a*b)  =  f(a)   +  f(b)

若f(b)   <  0    , 则有f(a*b) = f(a) + f(b)  < f(a)

进一步有下面的结论：  （记g[k]  =  gcd(a[1] , a[2] , a[3] , .... a[k] .）

若g[k]  < 0 , 则  f(a[1])  +  f(a[2] + .... +f(a[k])     <      f(a[1]/g[k])   +  f(a[2]/g[k])  + .....+ f(a[k]/g[k])

到这里题目已经很明显了 ， 这就是贪心策略！

代码：

#include <iostream>#include <cstdio>#include <cstring>#include <algorithm>#include <set>#include <cmath>using namespace std;const int maxn = 5050 ;typedef long long LL;const int num = 1e5 ;int prime[num/5] , pri_cnt ;bool flag[num+10] ;set<int>bad ;int a[maxn] , g[maxn] ;int n , m ;int gcd(int a,int b){ return b==0 ? a : gcd(b , a%b) ; }int f(int x){    if(x == 1) return 0 ;    int ret = 0;    for(int i=0 ; i<pri_cnt && prime[i]*prime[i]<=x ; i++) if(x % prime[i] == 0)    {        if(bad.count(prime[i]))        {            while(x % prime[i] == 0)  ret-- , x /= prime[i] ;        }        else        {            while(x % prime[i] == 0)  ret++ , x /= prime[i] ;        }    }    if(x > 1)    {        if(bad.count(x)) ret -- ;        else ret++ ;    }    return ret ;}int main(){    //freopen("in.txt" ,"r" ,stdin) ;    for(int i=2; i*i<=num ;i++) if(!flag[i]){        for(LL j = i*i ;j<=num ;j+=i) flag[j] = true ;    }    for(int i=2 ;i<=num ;i++)        if(!flag[i]) prime[pri_cnt++] = i ;    scanf("%d%d" , &n ,&m);    for(int i=1 ;i<=n ;i++)    {        scanf("%d" ,&a[i]) ;        g[i] = gcd(g[i-1] , a[i]) ;    }    for(int i=1 ;i<=m ;i++)    {        int x ;        scanf("%d" ,&x);        bad.insert(x) ;    }    int ans = 0 , s = 1;    for(int i=n ;i>=1; i--)    {        g[i] /= s;        if(f(g[i]) < 0) s*=g[i] ;        a[i] /= s ;        ans += f(a[i]) ;    }    printf("%d\n" ,ans) ;    return 0;}

E - Strictly Positive Matrix

给出一个a(i,j) >= 0 的矩阵A ， 问是否存在整数k使 A^k 的每个a(i , j)  > 0 均成立 。

模板题做多了，思维有点僵 ， 不太会变通。。

其实可以给出的是图的边 ，问是否存在这样的K， 在长度K的路径中，任意两点间均可到达 。

其实只要任意两点间可达（路径长度不限），那么这样的K就必然存在。

因为u到达v的路径长度可以是成周期性的 ， 那么当路径长度为所有周期的公倍数时，所有的点均两两可达 。

于是就转换为求强联通的问题了。

代码：

#include <iostream>#include <cstdio>#include <cstring>#include <algorithm>#include <stack>using namespace std;const int maxn = 2010 ;int edge[maxn][maxn] , cnt[maxn] ;int pre[maxn] , low[maxn] , sccno[maxn], dfs_clock , scc_cnt ;stack<int>S;void dfs(int u){    S.push(u) ;    pre[u] = low[u] = ++dfs_clock ;    for(int i=0; i<cnt[u] ;i++){        int v = edge[u][i] ;        if(!pre[v])        {            dfs(v) ;            low[u] = min(low[u] , low[v]) ;        }        else if(!sccno[v])        {            low[u] = min(low[u] , pre[v]) ;        }    }    if(low[u] == pre[u])    {        scc_cnt ++ ;        for(;;)        {            int x = S.top() ; S.pop() ;            sccno[x] = scc_cnt ;            if(x == u) break ;        }    }}int main(){    int n , x;    scanf("%d",&n);    for(int u=1 ;u<=n;u++)        for(int v=1;v<=n;v++)            if(scanf("%d",&x) , x) edge[u][cnt[u]++] = v;    for(int i=1; i<=n ;i++)        if(!pre[i]) dfs(i);    if(scc_cnt == 1) printf("YES\n") ;    else printf("NO\n") ;    return 0;}